BÀI TẬP KHÚC XẠ ÁNH SÁNG, PHẢN XẠ TOÀN PHẦN CÓ ĐÁP ÁN CHI TIẾT
| Bài tập 1: Một tia sáng truyền từ môi trường A vào môi trường B dưới góc tới là 90 thì góc khúc xạ là 80. Khi góc tới là 60 0 thì góc khúc xạ bằng
A. 50,40. B. 47,5 0. C. 46,30. D. 62,60 |
Lời giải chi tiết
Khi tia sáng truyền từ môi trường A vào môi trường B dưới góc tới là 9o thì góc khúc xạ là 8o
Ta có: nA sin 9o = nB sin8o (1)
Khi tia sáng truyền với góc tới i = 60o thì: nA sin 60o = nB sinr (2)
Lấy (2) chia cho (l) ta có: $\frac{\sin {{60}^{o}}}{\sin {{9}^{o}}}=\frac{snr}{\sin {{8}^{o}}}\Rightarrow \sin r=\sin {{8}^{o}}\frac{\sin {{60}^{o}}}{\sin {{9}^{o}}}=0,77\Rightarrow r=50,{{4}^{o}}.$Chọn A
| Bài tập 2: Một tia sáng truyền từ môi trường A vào môi trường B dưới góc tới là 90 thì góc khúc xạ là 80. Tính vận tốc truyền ánh sáng trong môi trường A biết vận tốc ánh sáng trong môi trường B là 200000km/s.
A. 224805,6km/s. B. 238539,7km/s. C. 177931,5km/s. D. 187956,8km/s |
Lời giải chi tiết
Theo định luật khúc xạ ánh sáng:${{n}_{A}}.\sin i={{n}_{B}}.\sin r\Rightarrow \frac{{{n}_{B}}}{{{n}_{A}}}=\frac{\sin i}{\sin r}$
Ta có: $\left\{ \begin{array}{} {{n}_{A}}=\frac{c}{{{v}_{A}}} \\ {} {{n}_{B}}=\frac{c}{{{v}_{B}}} \\ \end{array} \right.\Rightarrow \frac{{{n}_{B}}}{{{n}_{A}}}=\frac{{{v}_{A}}}{{{v}_{B}}}\Rightarrow{{v}_{A}}=\frac{{{n}_{B}}}{{{n}_{A}}}{{v}_{b}}=\frac{\sin i}{\sin r}{{v}_{B}}=\frac{\sin {{9}^{o}}}{\sin {{8}^{o}}}.200000=224805,6km/s.$ Chọn A
| Bài tập 3: Chiếu một tia sáng từ không khí vào nước với góc tới 300. Cho biết chiết suất của nước n= 4/3. Góc lệch D (góc giữa tia tới và tia khúc xạ) bằng
A. 220. B. 80. C. 68 0 . D. 600 |
Lời giải chi tiết
Vận dụng định luật khúc xạ ta có:
${{n}_{1}}\sin i={{n}_{2}}\sin r\Leftrightarrow 1.\sin {{30}^{0}}=\frac{4}{3}.\sin r$ 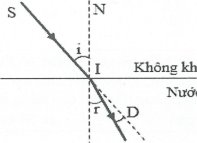
$\Rightarrow \sin r=\frac{3}{8}\Rightarrow r\approx {{22}^{0}}$
Góc lệch D: Từ hình vẽ ta có:
$D=i-r={{30}^{0}}-{{22}^{0}}={{8}^{0}}.$ Chọn B
| Bài tập 4: Cho một tia sáng đi từ môi trường nước ra môi trường không khí, tại điểm tới tia sáng tách thành hai phần, một phần phản xạ trở lại môi trường nước, một phần khúc xạ sang môi trường không khí. Biết chiết suất của nước với tia sáng bằng 4/3, và tia phản xạ vuông góc với tia khúc xạ. Góc giữa tia tới và pháp tuyến của mặt nước tại điểm tới (góc tới) bằng
A. 32056’ B. 36052’. C. 23065’. D. 53007’ |
Lời giải chi tiết
Gọi i, i’, r lần lượt là góc tới, góc phản xạ và góc khúc xạ
Theo định luật phản xạ ánh sáng có i’ = i
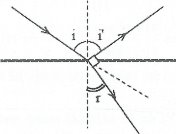
Có: ${{\text{i}}^{\text{ }\!\!’\!\!\text{ }}}+r={{90}^{0}}\Rightarrow i+r={{90}^{0}}\Rightarrow \sin r=\cos i.$
Theo định luật khúc xạ ánh sáng: $\frac{4}{3}\sin i=\sin r$
$\Leftrightarrow \frac{\sin i}{\sin r}=\frac{3}{4}\Leftrightarrow \frac{\sin i}{\cos i}=\frac{3}{4}\Leftrightarrow \tan i=\frac{3}{4}\Rightarrow i\approx {{36}^{0}}{{52}^{‘}}$ Chọn B
| Bài tập 5: Một chậu hình hộp chữ nhật đựng chất lỏng. Biết AB =a, AD = 2a. Mắt nhìn theo phướng BD nhìn thấy được trung điểm M của BC. Chiết suất của chất lỏng bằng
A.1,5 B. 1,33 C.1,54 D. 1,26 |
Lời giải chi tiết
Khi mắt nhìn theo phương BD thấy được điểm M nghĩa là tia sáng từ M qua D sẽ đến được mắt, hay tia tới theo phương MD và tia khúc xạ theo phương BD.
Theo định luật khúc xạ ánh sáng, ta có:$\frac{\sin i}{\sin r}=\frac{1}{n}\Rightarrow n=\frac{\sin r}{\sin i}$
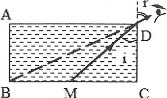
Với:$\sin i=\frac{MC}{MD}=\frac{a}{a\sqrt{2}}=\frac{\sqrt{2}}{2}$
$\sin r=\sin BDC=\frac{BC}{BD}=\frac{2a}{\sqrt{4{{a}^{2}}+{{a}^{2}}}}=\frac{2}{\sqrt{5}}$
$\Rightarrow n=\frac{\frac{2}{\sqrt{5}}}{\frac{\sqrt{2}}{2}}=\frac{4}{\sqrt{10}}=1,26.$ Chọn D
| Bài tập 6: Một bể chứa nước có thành cao 80cm và đáy phẳng dài 120cm. Độ cao mực nước trong bể là 60cm, chiết suất của nước là 4/3. Ánh nắng chiếu theo phương nghiêng 1 góc 300 so với phương ngang. Độ dài của bóng đen tạo thành dưới đáy bể xấp xỉ dài
A. 86 cm. B. 54 cm. C. 78 cm. D. 93 cm |
Lời giải chi tiết
Ánh nắng chiếu nghiêng 1 góc 300 so với phương ngang nên$\Rightarrow i={{60}^{0}}$
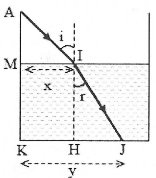
Từ hình vẽ ta có: $\tan i=\frac{x}{MA}\Rightarrow x=MA.\tan 60=20\sqrt{3}cm$
Cũng từ hình vẽ lại có $\sin r=\frac{HJ}{\sqrt{H{{I}^{2}}+H{{J}^{2}}}}\Rightarrow \frac{\sin i}{\sin r}=n$
$\Leftrightarrow \frac{\sqrt{3}}{2}\frac{\sqrt{H{{I}^{2}}+H{{J}^{2}}}}{H{{J}^{2}}}=n$
$\Leftrightarrow \frac{3}{4}\left( \frac{{{60}^{2}}+H{{J}^{2}}}{H{{J}^{2}}} \right)=\frac{16}{9}\Rightarrow HJ=85,9cm$. Chọn A
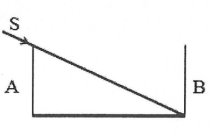
Bài tập 7: Một cái máng nước sâu 20 cm, rộng 40 cm có hai thành bên thẳng đứng. Ðúng lúc máng cạn nước thì bóng râm của thành A kéo dài tới đúng chân thành B đối diện. Người ta đổ nước vào máng đến một độ cao h thì bóng cùa thành A ngắn bớt đi 7 cm so với trước. Biết chiết suất của nước là n = 4/3, h bằng A. 14 cm. B. 13 cm. C. 12 cm. D. 11 cm. |
Lời giải chi tiết
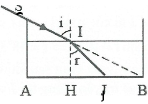
Trước khi đổ nước, bóng của thành A là AB, sau khi đổ nước, bóng của thành A là AJ.
Ta có: $\text{tani }=\frac{HB}{HI}\text{ }\Rightarrow \text{HB}=\text{HI}\text{.tani = h}\text{.tani}\text{.}$
$\text{tanr}=\frac{\text{HJ}}{\text{HI}}\Rightarrow HJ=HI.\tan r=h.\tan r$
Theo đề:AB – AJ = HB – HJ = 7cm.
$\Leftrightarrow h.\tan i-h.\tan r=h(\tan i-\tan r)=7$
$\Rightarrow h-\frac{7}{\tan i-\tan r}$
Mặt khác: $\begin{array}{} \sin i=\frac{AB}{SB}=\frac{AB}{\sqrt{A{{S}^{2}}+A{{B}^{2}}}}=\frac{40}{\sqrt{{{30}^{2}}+{{40}^{2}}}}=0,8 \\ {} \operatorname{Cos}i=0,6v\grave{a}tai=0,8\frac{3}{4=0,6}\Rightarrow \cos r=0,8\tanr=\frac{0,6}{0,8}=\frac{3}{4}\Rightarrow h=\frac{7}{\frac{4}{3}-\frac{3}{4}}=12cm \\ \end{array}$
$\Rightarrow cosi=0,6$ và $\tan i=\frac{0,8}{0,6}=\frac{4}{3}$
$\tan i=0,8\frac{3}{4}=0,6\Rightarrow \cos r=0,8;\tan r=\frac{0,6}{0,8}=\frac{3}{4}\Rightarrow h=\frac{7}{\frac{4}{3}-\frac{3}{4}}=12cm$. Chọn C
| Bài tập 8: Một viên sỏi nằm dưới đáy của một bể có mực nước sâu 0,6 m, một em bé cầm một cái thanh thẳng và ngắm viên sỏi dưới góc 45 0 so với mặt nước rồi đâm cái thanh theo đúng hướng đó xuống đáy bể. Khi chạm đáy bể, đầu thanh së cách viên sỏi một khoảng bao nhiêu?
A. 0,23 m. B. 0,15 m. C. 0,37 m. D. 0,25 m |
Lời giải chi tiết
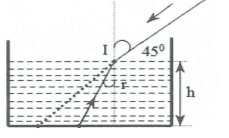
Tia sáng phát ra từ viên sỏi S đến mặt nuước tại I và khúc xạ ra không khí dưới góc độ 450. Cậu bé dã ngắm theo hướng của tia sáng này nên khi đưa thanh theo hướng đã ngắm thì đầu thanh sẽ chạm đáy bể tại S như hình bên. Gọi r là góc tới tại mặt nước thì theo định luật khúc xạ, ta xác định được góc này :
$\sin {{45}^{0}}=1,33\sin r\Rightarrow r\approx {{32}^{0}}$
Do góc ngắm là 450 nên HS’ = h – 0,6m
Ngoài ra SH = h tan r =0,37m
Nên suy ra được đoạn lệch của đầu thanh khỏi viên sỏi:
$S’S=S’H-SH=0,23m$. Chọn A
| Bài tập 9: Cho một khối thủy tinh dạng bán cầu có bán kính R, chiết suất n = 1,5. Chiếu thẳng góc tới mặt phẳng của bán cầu một tia sáng SI. Biết điểm tới I cách tâm O của khối bán cầu đoạn R/2. Góc lệch của tia tới và tia ló ra khỏi bản thủy tinh bằng
A. 140 28′ B. 180 36′. C. 48 036′. D. 320 15′ |
Lời giải chi tiết
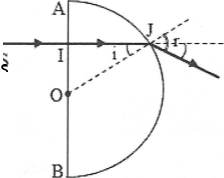
Tia sáng di thẳng qua mặt phẳng AB của khối bán cầu, tới mặt cầu tại J vói góc tới là i.
Ta có:
$\sin i=\frac{OI}{OJ}=\frac{1}{2}\Rightarrow i={{30}^{0}}$
Tại J ta có: $\text{nsini = sin r}\Leftrightarrow \text{ l, 5 sin 30 = sin r }$
$\Rightarrow \text{ sin}\,\text{r = 0,75}\Rightarrow \text{r = 4}{{\text{8}}^{\text{0}}}36’$
Như vậy tia sáng sau khi chiếu thẳng góc tới mặt phẳng của bán cầu së truyền thẳng tới J và cuối cùng khúc xạ ra ngoài.
Góc lệch của tia tới và tia ló ra khỏi bản thủy tinh bằng $\text{4}{{\text{8}}^{\text{0}}}36′-30={{18}^{0}}36’$. Chọn B
| Bài tập 10: Có 3 môi trường trong suốt. Với cùng góc tới i: nếu tia sáng truyền từ (l) vào (2) thì góc khúc xạ là 300, truyền từ (l) vào (3) thì góc khúc xậ là 450. Góc giới hạn phản xạ toàn phần ở mặt phân cách (2) và (3) là
A. 420. B. 450. C. 480. D. 370 |
Lời giải chi tiết
$(\text{l) sang (2):}{{\text{n}}_{\text{1}}}\text{sini = }{{\text{n}}_{\text{2}}}\text{ sin 3}{{\text{0}}^{\text{0}}}(*)$
$(\text{l) sang (3):}{{\text{n}}_{\text{1}}}\text{sini = }{{\text{n}}_{\text{3}}}\text{ sin 4}{{\text{5}}^{\text{0}}}(**)$
Từ (*) và (**) ta có: ${{\text{n}}_{\text{2}}}\text{ sin 3}{{\text{0}}^{\text{0}}}={{n}_{3}}\sin {{45}^{0}}\Leftrightarrow \frac{{{n}_{2}}}{2}=\frac{{{n}_{3}}}{\sqrt{2}}\Rightarrow \frac{{{n}_{2}}}{{{n}_{3}}}=\sqrt{2}(***)$
Từ (***) ta thấy n2 > n3 nên chỉ xảy ra phản xạ toàn phần khi ánh sáng truyền từ (2) sang (3).
Vậy góc giới hạn phản xạ toàn phần ở mặt phân cách (2) và (3) là: $\sin {{i}_{gh}}=\frac{{{n}_{3}}}{{{n}_{2}}}=\frac{1}{\sqrt{2}}\Rightarrow {{i}_{gh}}={{45}^{0}}.$ Chọn B
| Bài tập 11: Một miếng gỗ hình tròn, bán kính 5 (cm). Ở tâm O, cắm thẳng góc một đinh OA. Thả miếng gỗ nỗi trong một chậu nước có chiết suất n = 4/3. Ðinh OA ở trong nước, cho OA = 8 (cm). Mắt đặt trong không khí sẽ thấy đầu A cách mặt nước một khoảng lớn nhất là
A. OA’ = 3,5 (cm). B. OA’ = 4,4 (cm). C. OA’ = 6,9 (cm). D. OA’ = 8,7 (cm). |
Lời giải chi tiết
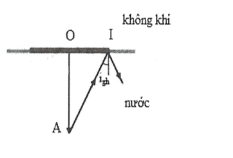
Mắt không thấy đầu A khi tia sáng từ A tới mặt nước tại I (mép miếng gỗ) xảy ra phản xạ toàn phần:
$\sin {{i}_{gh}}=\frac{1}{n}=\frac{1}{4/3}\Rightarrow 48,{{59}^{0}}$
Ta có: $i\ge {{i}_{gh}}$ và $OA=R/\tan i$
$O{{A}_{\max }}=\frac{R}{\tan {{i}_{gh}}}=\frac{5}{\tan 48,{{59}^{0}}}=4,4cm$. Chọn B
| Bài tập 12: Một tia sáng được chiếu vào mặt bên cùa một lăng kính dưới góc tới nhỏ. Biết vận tốc của tia này trong lăng kính là l,98.108 m/s. Sau khi qua lăng kính, tia ló lệch so vói tia tới một góc bằng 50 . Góc chiết quang của lăng kính bằng
A. 6,80. B. 7,50. C. 9,700. D. 11,80 |
Lời giải chi tiết
Ta có: $n=\frac{c}{v}=\frac{{{3.10}^{8}}}{1,{{98.10}^{8}}}\approx 1,5152$
Vì góc chiết quang A và góc tới i là những góc nhỏ nên góc lệch lúc đó là:
$D=(n-1)A\Rightarrow A=\frac{D}{n-1}=\frac{5}{0,5152}=9,{{7}^{0}}$. Chọn C
| Bài tập 13: Một lăng kính có chiết suất n. Khi chiếu tới mặt bên một chùm tia đơn sắc với góc tới il = 600 thì
i2 = 300 và góc lệch D = 450 . Chiết suất n bằng A. 0,88. B. 1,3. C. 1 ,8. D. 2,5 |
Lời giải chi tiết
Từ $D={{i}_{1}}+{{i}_{2}}-A\Rightarrow A={{i}_{1}}+{{i}_{2}}-D={{45}^{0}}$
Từ $\sin {{i}_{1}}=n\sin \,{{r}_{1}}\Rightarrow \sin {{r}_{1}}=\frac{\sin {{i}_{1}}}{n}=\frac{\sin {{60}^{0}}}{n}=\frac{\sqrt{3}}{2n}$
Từ $\sin {{i}_{2}}=n\sin {{r}_{2}}\Rightarrow \sin {{r}_{2}}=\frac{\sin {{i}_{2}}}{n}=\frac{\sin {{30}^{0}}}{n}=\frac{1}{2n}\Rightarrow \cos {{r}_{2}}=\frac{\sqrt{4{{n}^{2}}-1}}{2n}$
Từ $A={{r}_{1}}+{{r}_{2}}\Rightarrow {{r}_{1}}=A-{{r}_{2}}\Rightarrow \sin {{r}_{1}}=\sin (A-{{r}_{2}})$
$\Rightarrow \sin {{r}_{1}}=\sin A.\cos {{r}_{2}}-\cos A.\sin {{r}_{2}}$
Thay vào ta có: $\frac{\sqrt{3}}{2n}=\frac{\sqrt{2}}{2}.\frac{\sqrt{4{{n}^{2}}-1}}{2n}-\frac{\sqrt{2}}{2}.\frac{1}{2n}\Rightarrow n=1,8.$ Chọn C
| Bài tập 14: Một lăng kính có góc chiết quang A. Chiếu tia sáng SI đến vuông góc vói mặt bên của lăng kính. Biết góc lệch của tia ló và tia tới là D = 150 . Cho chiết suất của lăng kính là n = 1,5. Góc chiết quang A xấp xỉ bằng
A. 300 . B. 260. C. 240. D. 320. |
Lời giải chi tiết
Vì chiếu tia tới vuông góc vói mặt nên ${{\text{i}}_{1}}\text{ = 0 }\Rightarrow {{\text{r}}_{\text{1}}}=0$
Ta có: $A={{r}_{1}}+{{r}_{2}}\Rightarrow A={{r}_{2}}$
Mà: $D={{i}_{1}}+{{i}_{2}}-A\Leftrightarrow 15=0+{{i}_{2}}-A\Leftrightarrow {{i}_{2}}=15+A$
Lại có: $\sin {{i}_{2}}=n\sin {{r}_{2}}\Leftrightarrow \sin (15+A)\Leftrightarrow 1,5\sin A$
$\Leftrightarrow \sin 15\cos A+\sin A\cos 15=1,5\sin A\Leftrightarrow \sin 15\cos A=(1,5-\cos 15)\sin A$
$\Leftrightarrow \tan A=\frac{\sin 15}{(1,5-\cos 15)}\Rightarrow A\approx 25,{{85}^{0}}.$ Chọn B
| Bài tập 15: Lăng kính có góc chiết quang A = 600 và chiết suất $n=\sqrt{3}$ đối với ánh sáng đơn sắc. Góc lệch đặt giá trị cực tiểu khi góc tới
A. 45 0. B. 600. C. 15 0 . D. 300 |
Lời giải chi tiết
Khi có góc lệch cực tiểu xảy ra, tia ló và tia tới đối xứng nhau qua mặt phân giác của góc chiết quang
$A\Rightarrow {{r}_{1}}-{{r}_{2}}=\frac{A}{2}=\frac{{{60}^{0}}}{2}={{30}^{0}}$
Từ $\sin {{i}_{1}}=n\sin {{r}_{1}}\Rightarrow \sin {{i}_{1}}=\sqrt{3}.\sin {{30}^{0}}=\frac{\sqrt{3}}{2}\Rightarrow {{i}_{1}}={{60}^{0}}.$ Chọn B
| Bài tập 16: Một lăng kính tam giác ABC đều, đặt trong không khí. Khi chiếu ánh sáng đơn sắc với góc tới bằng góc ló thì góc lệch D =300. Chiết suất tỉ đối của chất làm lăng kính với môi trường là
A. 1,61 B. 1,51 C. 1,41 D. 1,31 |
Lời giải chi tiết
Khi góc tới bằng góc ló thì góc lệch đạt cực tiểu: Dmin = 300
Từ $\sin \frac{{{D}_{\min }}+A}{2}=n\sin \frac{A}{2}\Rightarrow n=\frac{\sin \frac{{{30}^{0}}+{{60}^{0}}}{2}}{\sin \frac{{{60}^{0}}}{2}}=\frac{\sin {{45}^{0}}}{\sin {{30}^{0}}}=\sqrt{2}.$ Chọn C
| Bài tập 17: Qua một lăng kính có chiết suất $n=\sqrt{3}$ và góc chiết quang A. Tia sáng đơn sắc sau khi khúc xạ qua lăng kính cho tia ló có góc lệch cực tiểu đúng bằng A. Nếu nhúng lăng kính này vào nước có chiết suất ${{n}_{nc}}=\frac{4}{3}$ thì góc lệch cực tiểu lúc này bằng
A. 320 B. 210 C. 300 D. 170 |
Lời giải chi tiết
Khi: ${{D}_{\min }}\Rightarrow \left\{ \begin{matrix}{{r}_{1}}={{r}_{2}}=\frac{A}{2} \\{{i}_{1}}={{i}_{2}}=i \\\end{matrix}\Rightarrow {{D}_{\min }}=2i-A\Leftrightarrow A=2i-A\Rightarrow i=A \right.$
Ta có: $\sin i=n\sin r\Leftrightarrow \sin A=\sqrt{3}\sin \frac{A}{2}\Leftrightarrow 2\sin \frac{A}{2}\cos \frac{A}{2}=\sqrt{3}\sin \frac{A}{2}$
$\Leftrightarrow \cos \frac{A}{2}=\frac{\sqrt{3}}{2}\Rightarrow A={{60}^{0}}\Rightarrow \left\{ \begin{matrix}{{r}_{1}}={{r}_{2}}=\frac{A}{2}={{30}^{0}} \\{{i}_{1}}={{i}_{2}}=i \\\end{matrix} \right.$
Ta có: $\sin i=\frac{{{n}_{lk}}}{{{n}_{nc}}}\sin {{30}^{0}}\Leftrightarrow \sin i=\frac{\sqrt{3}}{4/3}\sin {{30}^{0}}=\frac{3\sqrt{3}}{8}\Rightarrow i=40,{{5}^{0}}.$
Góc lệch cực tiểu khi đó: ${{D}_{\min }}=2i-A={{21}^{0}}$. Chọn B.
|
Bài tập 18: Cho một lăng kính thủy tinh đặt trong không khí với góc chiết quang bằng 600 và chiết suất của thủy tinh bằng 1,6. Một tia sáng đi trong mặt phẳng vuông góc với cạnh của lăng kính, qua mặt bên thứ nhất của lăng kính với góc tới i1. Để tia sáng bị phản xạ toàn phần tại mặt thứ hai của lăng kính thì góc tới i1 phải thõa mãn điều kiện A. il < 35 034′. B. il > 35 034′. C. il < 38040′ D. il > 38040′ |
Lời giải
Góc giới hạn xảy ra hiện tượng phản xạ toàn phần mặt 2: $\sin {{r}_{2gh}}=\frac{1}{1,6}\Rightarrow {{r}_{2gh}}=38,{{68}^{0}}$
Phản xạ toàn phần tại mặt 2 thì ${{r}_{2}}>{{r}_{2gh}}$
Mà ${{r}_{1}}+{{r}_{2}}=A\Rightarrow A-{{r}_{1}}>{{r}_{2gh}}$
$\Rightarrow {{r}_{1}}<A-{{r}_{2gh}}$
$\Rightarrow \sin {{r}_{1}}<\sin (A-{{r}_{2gh}})$
Tại mặt 1: $\sin {{i}_{1}}=n.\sin {{r}_{1}}\Rightarrow \frac{\sin {{r}_{1}}}{n}<\sin (A-{{r}_{2gh}})$
$\Rightarrow \sin {{i}_{1}}<n.\sin (A-{{r}_{2gh}})=1,6\sin ({{60}^{0}}-38,{{68}^{0}})=0,58\Rightarrow {{i}_{1}}<{{35}^{0}}{{34}^{‘}}$. Chọn A.
|
Bài tập 19: Chiếu một chùm sáng hẹp song song tới một lăng kính có góc chiết quang bé sao cho chùm tia tới đúng cạnh của lăng kính và chỉ một phần của chùm tới đi qua lăng kính, phần còn lại tiếp tục truyền thẳng. Biết lăng kính có góc chiết quang bằng 80 và chiết suất bằng 1,5. Đặt một màn chắn sogn song với mặt phẳng phân giác góc chiết quang và cách lăng kính một khoảng bằng 1m thì thấy có hai vết sáng nhỏ trên màn. Khoảng cách giữa hai vết sáng xấp xỉ bằng A. 7 cm B. 4 cm C. 5,5 cm D. 35mm |
Lời giải
$A={{8}^{0}}=2\pi /45rad$
Góc lệch của chùm tia tới và tia ló:
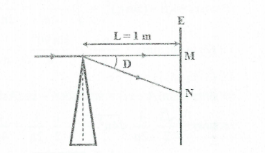
$D=(n-1)A=(1,5-1).\frac{2\pi }{45}=\frac{\pi }{45}rad$
Khoảng cách giữa hai vệt sáng:
$MN=L.\tan D\approx L.{{D}_{rad}}=\pi /45.1\approx {{70.10}^{-3}}m=7cm$
Chọn A
|
Bài tập 20: Một lăng kính thủy tinh có chiết suất n = 1,6. Chiếu một tia sáng theo phương vuông góc mặt bên của lăng kính. Tia sáng phản xạ toàn phần ở mặt bên thứ hai. Giá trị nhỏ nhất của A bằng A. 42013’ B. 27036’ C. 38041’ D. 29047’ |
Lời giải
Tia tới SI vuông góc AB, truyền thẳng gặp mặt AC tại J với góc tới I =A (góc có cạnh tương ứng vuông góc). Ta có:$\sin {{i}_{gh}}=\frac{1}{n}$
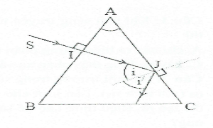
Vì tia sáng phản xạ toàn phần tai J nên $i\ge {{i}_{gh}}$
$\Rightarrow \sin A=\sin i\ge \sin {{i}_{gh}}=\frac{1}{n}=\frac{1}{1,6}=0,625\Rightarrow \sin A\ge \sin {{38}^{0}}{{41}^{‘}}$
$\Rightarrow A\ge {{38}^{0}}{{41}^{‘}}\Rightarrow {{A}_{\min }}={{38}^{0}}{{41}^{‘}}$. Chọn C.
|
Bài tập 21: Một lăng kính có tiết diện vuông góc với một tam giác đều ABC. Một chùm tia sáng đơn sắc hẹp SI được chiếu tới mặt AB trong mặt phẳng của tiết diện vuông góc và theo phương vuông góc với đường cao AH của ABC. Chùm tia ló khỏi mặt AC theo phương sát với mặt này. Chiết suất của lăng kính bằng A. 1,41 B. 1,73 C. 1,37 D. 1,53 |
Lời giải
Áp dụng các công thức về lăng kính, ta có:
$\sin {{i}_{1}}=n\sin {{r}_{1}}(1)$
$\sin {{i}_{2}}=n\sin {{r}_{2}}(2)$
${{r}_{1}}+{{r}_{2}}=A(3)$
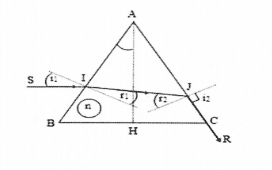
Vì tia tới SI vuông góc với đường cao AH nên ta có:
${{i}_{1}}=\frac{A}{2}=\frac{60}{2}={{30}^{0}}$(góc có canh tương ứng vuông góc)
Tia ló JR theo phương sát với mặt AC nên ${{i}_{2}}={{90}^{0}}$
Từ (1) ta có: $\sin {{r}_{1}}=\frac{\sin {{i}_{1}}}{n}=\frac{\sin {{30}^{0}}}{n}=\frac{1}{2n}$
$\Rightarrow \cos {{r}_{1}}=\sqrt{1-{{(\sin {{r}_{1}})}^{2}}}=\sqrt{1-\frac{1}{4{{n}^{2}}}}=\frac{1}{2n}\sqrt{4{{n}^{2}}-1}$
Từ (2) ta có: $\sin {{r}_{2}}=\frac{\sin {{i}_{2}}}{n}=\frac{\sin {{90}^{0}}}{n}=\frac{1}{n}(4)$
Từ (3) ta có: ${{r}_{2}}=A-{{r}_{1}}$
$\Rightarrow \sin {{r}_{2}}=\sin (A-{{r}_{1}})=\sin A\cos {{r}_{1}}-\cos A\sin {{r}_{1}}=\sin {{60}^{0}}\cos {{r}_{1}}-\cos {{60}^{0}}\sin {{r}_{1}}$
$\Rightarrow \sin {{r}_{2}}=\frac{\sqrt{3}}{2}.\frac{1}{2n}\sqrt{4{{n}^{2}}-1}-\frac{1}{2}.\frac{1}{2n}=\frac{1}{4n}\left[ \sqrt{3(4{{n}^{2}}-1)}-1 \right](5)$
Từ (4) và (5), ta có: $\frac{1}{4n}\left[ \sqrt{3(4{{n}^{2}}-1)}-1 \right]=\frac{1}{n}.$
$\Rightarrow \left[ \sqrt{3(4{{n}^{2}}-1)}-1 \right]=4\Rightarrow n=\sqrt{\frac{7}{3}}=1,53$. Chọn D.