Tính Góc giữa mặt bên và mặt đáy – bài tập có đáp án chi tiết
Phương pháp xác định góc giữa mặt bên và mặt đáy
Tính góc giữa mặt phẳng (SAB) và mặt phẳng đáy (ABC).
Dựng đường cao $SH\bot \left( ABC \right)$, dựng $HE\bot AB.$
Khi đó $AB\bot \left( SEH \right)\Rightarrow \widehat{\left( \left( SAB \right);\left( ABC \right) \right)}=\widehat{SEH}.$
Bài tập góc giữa mặt bên và mặt đáy có đáp án
| Bài tập 1: Cho hình chóp S.ABCD có $SA\bot \left( ABCD \right)$, đáy là hình chữ nhật ABCD với $AB=a;AD=a\sqrt{3}.$ Biết rằng mặt phẳng (SCD) tạo với đáy một góc $60{}^\circ .$
a) Tính cosin góc tạo bởi mặt phẳng (SBC) và mặt đáy (ABCD). b) Tính tan góc giữa mặt phẳng (SBD) và mặt đáy (ABCD). |
Lời giải chi tiết
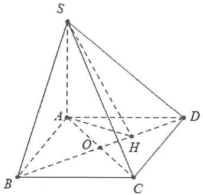
a) Do $\left\{ \begin{array} {} CD\bot SA \\ {} CD\bot D \\ \end{array} \right.\Rightarrow CD\bot \left( SDA \right)$ do đó góc giữa mặt phẳng (SCD) và đáy là $\widehat{SDA}=60{}^\circ $
Suy ra $SA=AD\tan 60{}^\circ =3a.$
Do $\left\{ \begin{array} {} BC\bot SA \\ {} BC\bot AB \\ \end{array} \right.\Rightarrow BC\bot \left( SBA \right)\Rightarrow \widehat{\left( \left( SBC \right);\left( ABC \right) \right)}=\widehat{SBA}$
Mặt khác $\cos \widehat{SBA}=\frac{AB}{SB}=\frac{AB}{\sqrt{S{{A}^{2}}+A{{B}^{2}}}}=\frac{a}{\sqrt{9{{a}^{2}}+{{a}^{2}}}}=\frac{1}{\sqrt{10}}.$
Vậy $\cos \widehat{\left( \left( SBC \right);\left( ABC \right) \right)}=\frac{1}{\sqrt{10}}.$
b) Dựng $AH\bot BD\Rightarrow BD\bot \left( SHA \right)\Rightarrow \widehat{\left( \left( ABD \right);\left( ABC \right) \right)}=\widehat{SHA}$
Lại có: $AH=\frac{AB.AD}{\sqrt{A{{B}^{2}}+A{{D}^{2}}}}=\frac{a\sqrt{3}}{2}.$
Suy ra $\tan \widehat{\left( \left( SBD \right);\left( ABCD \right) \right)}=\tan \widehat{SHA}=\frac{SA}{AH}=2\sqrt{3}.$
| Bài tập 2: Cho khối chóp S.ABC có đáy ABC là tam giác vuông tại B có $AB=a\sqrt{3};BC=a$, tam giác SAC là tam giác cân tại S và thuộc mặt phẳng vuông góc với đáy. Biết đường thẳng SB tạo với đáy một góc $60{}^\circ $. Tính góc $\widehat{\left( \left( SBC \right);\left( ABC \right) \right)}.$ |
Lời giải chi tiết
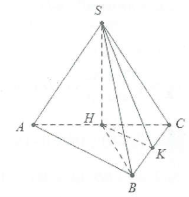
Gọi H là trung điểm của AC, do tam giác SAC cân nên ta có:
$SH\bot AC.$ Mặt khác $\left( SAC \right)\bot \left( ABCD \right)$ nên $SH\bot \left( ABC \right).$
Khi đó: $\widehat{\left( SB;\left( ABC \right) \right)}=\widehat{SBH}=60{}^\circ .$
Ta có: $AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=2a\Rightarrow BH=\frac{1}{2}AC=a.$
Khi đó: $SH=a\tan 60{}^\circ =a\sqrt{3}.$
Dựng $HK\bot BC\Rightarrow BC\bot \left( SHK \right).$
$\Rightarrow \widehat{SKH}=\widehat{\left( \left( SBC \right);\left( ABC \right) \right)}$, trong đó ta có: $HK=\frac{AB}{2}=\frac{a\sqrt{3}}{2};$
$SH=a\sqrt{3}\Rightarrow \cos \widehat{SKH}=\frac{1}{\sqrt{5}}.$
Vậy $\widehat{\left( \left( SBC \right);\left( ABC \right) \right)}=\varphi $ với $\cos \varphi =\frac{1}{\sqrt{5}}.$
| Bài tập 3: Cho hình chóp S.ABCD có đáy ABCD là hình thoi, có $AB=2a$ và góc $\widehat{BAD}=120{}^\circ $. Hình chiếu vuông góc của S xuống mặt phẳng đáy (ABCD) trùng với giao điểm I của hai đường chéo và $SI=\frac{a}{2}$. Tính góc tạo bởi mặt phẳng (SAB) và mặt phẳng (ABCD). |
Lời giải chi tiết
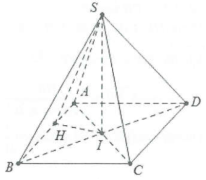
Gọi $\varphi $ là góc giữa hai mặt phẳng (SAB) và mặt phẳng (ABCD). Gọi H là hình chiếu vuông góc của I trên AB.
Ta có: $\left\{ \begin{array} {} AB\bot HI \\ {} AB\bot SI \\ \end{array} \right.\Rightarrow AB\bot \left( SHI \right).$
Do đó $\varphi =\widehat{\left( SH;IH \right)}=\widehat{SHI}.$
Do $\widehat{BAD}=120{}^\circ \Rightarrow \widehat{BAI}=60{}^\circ \Rightarrow \Delta ABC$ đều cạnh 2a nên $IA=a\Rightarrow IH=IA\sin \widehat{IAB}=IA\sin 60{}^\circ =\frac{a\sqrt{3}}{2}.$
Do đó $\tan \varphi =\frac{SI}{IH}=\frac{1}{\sqrt{3}}\Rightarrow \varphi =30{}^\circ .$
| Bài tập 4: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B có $AD=2a$ và $AB=BC=a$. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Biết mặt phẳng (SBC) tạo với đáy (ABCD) một góc 60°. Tính tan góc tạo bởi mặt phẳng (SCD) và (SBD) với mặt phẳng (ABCD). |
Lời giải chi tiết
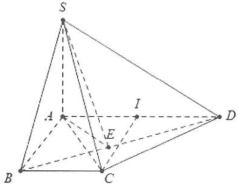
Ta có: $\left\{ \begin{array} {} BC\bot AB \\ {} BC\bot SA \\ \end{array} \right.\Rightarrow BC\bot \left( SBA \right).$
Khi đó: $\widehat{\left( \left( SBC \right);\left( ABCD \right) \right)}=\widehat{SBA}=60{}^\circ $
$\Rightarrow SA=AB\tan 60{}^\circ =a\sqrt{3}.$
Gọi I là trung điểm của AD $\Rightarrow $ ABCI là hình vuông cạnh a $\Rightarrow CI=a=\frac{1}{2}AD\Rightarrow \Delta ACD$ vuông tại C.
Ta có: $\left\{ \begin{array} {} CD\bot AC \\ {} CD\bot SA \\ \end{array} \right.\Rightarrow CD\bot \left( SCA \right).$
Do đó $\widehat{\left( \left( SCD \right);\left( ABCD \right) \right)}=\widehat{\left( SC;AC \right)}=\widehat{SCA}$ và $\tan \widehat{SCA}=\frac{SA}{AC}=\frac{a\sqrt{3}}{\sqrt{A{{B}^{2}}+B{{C}^{2}}}}=\sqrt{\frac{3}{2}}=\frac{\sqrt{6}}{2}.$
Dựng $AE\bot BD$, lại có $BD\bot SA\Rightarrow BD\bot \left( SEA \right)\Rightarrow \widehat{\left( \left( SBD \right);\left( ABCD \right) \right)}=\widehat{SEA}.$
Ta có: $AE=\frac{AB.AD}{\sqrt{A{{B}^{2}}+A{{D}^{2}}}}=\frac{2a}{\sqrt{5}}\Rightarrow \tan \widehat{SEA}=\frac{SA}{AE}=\frac{\sqrt{15}}{2}.$
| Bài tập 5: Cho hình lăng trụ $ABC.{A}'{B}'{C}’$ có đáy là tam giác đều cạnh 2a. Hình chiếu vuông góc của ${A}’$ lên mặt phẳng (ABC) là trung điểm của cạnh AB, góc giữa đường thẳng ${A}’C$ và mặt đáy (ABC) bằng $60{}^\circ $. Tính cosin góc giữa mặt phẳng $\left( {A}’AC \right)$ và mặt đáy (ABC). |
Lời giải chi tiết
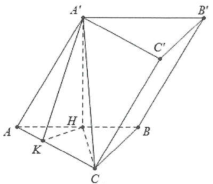
Gọi H là trung điểm cạnh AB ta có: ${A}’H\bot \left( ABC \right)$
Do đó $\widehat{{A}’CH}=60{}^\circ .$ Lại có: $CH=AC\sin 60{}^\circ =a\sqrt{3}$
$\Rightarrow {A}’H=CH\tan 60{}^\circ =3a.$
Dựng $HK\bot AC$ ta có ${A}’H\bot AC\Rightarrow \left( {A}’HK \right)\bot AC.$
Khi đó: $HK=HA\sin 60{}^\circ =\frac{a\sqrt{3}}{2}.$
Ta có: $\cos \widehat{{A}’KH}=\frac{HK}{\sqrt{H{{K}^{2}}+{A}'{{H}^{2}}}}=\frac{1}{\sqrt{13}}>0.$
Do vậy $\cos \widehat{\left( \left( {A}’AC \right);\left( ABC \right) \right)}=\frac{1}{\sqrt{13}}.$
