Hàm số lũy thừa là gì? Lý thuyết, tập xác định, đạo hàm, đồ thị, tính chất
1. Định nghĩa: hàm số lũy thừa là gì?
Hàm số $y={{x}^{\alpha }}$ với $\alpha \in \mathbb{R},$ được gọi là hàm số lũy thừa.
2. Tập xác định của hàm số lũy thừa
Tập xác định của hàm số $y={{x}^{\alpha }}$ là:
- $\mathbb{R}$ với $\alpha $ là số nguyên dương
- $\mathbb{R}\backslash \left\{ 0 \right\}$ với $\alpha $ là số nguyên âm hoặc bằng 0.
- $\left( 0;+\infty \right)$ với $\alpha $ không nguyên.
3. Đạo hàm của hàm số lũy thừa
Hàm số $y={{x}^{\alpha }}$ với $\alpha \in \mathbb{R}$ có đạo hàm với mọi $x>0$ và $\left( {{x}^{\alpha }} \right)’=\alpha .{{x}^{\alpha -1}}$
4. Tính chất của hàm số lũy thừa trên khoảng $\left( 0;+\infty \right)$
- $y={{x}^{\alpha }}>0$ $\left( \forall x\in \left( 0;+\infty \right) \right)$
- Đồ thị hàm số luôn đi qua điểm $\left( 1;1 \right)$
- Khi $\alpha >0\Rightarrow y’=\left( {{x}^{\alpha }} \right)’=\alpha .{{x}^{\alpha -1}}>0$ $\left( \forall x\in \left( 0;+\infty \right) \right)$ hàm số luôn đồng biến
Trong trường hợp này $\underset{x\to +\infty }{\mathop{\lim }}\,{{x}^{\alpha }}=+\infty ;\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,{{x}^{\alpha }}=0$ do đó đồ thị hàm số không có đường tiệm cận
- Khi $\alpha <0\Rightarrow y’=\left( {{x}^{\alpha }} \right)’=\alpha .{{x}^{\alpha -1}}<0$ $\left( \forall x\in \left( 0;+\infty \right) \right)$ hàm số luôn nghịch biến
Trong trường hợp này $\underset{x\to +\infty }{\mathop{\lim }}\,{{x}^{\alpha }}=0;\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,{{x}^{\alpha }}=+\infty $ do đó đồ thị hàm số nhận trục $Ox$ là đường tiệm cận ngang và trục $Oy$ là đường tiệm cận đứng.
5. Đồ thị hàm số lũy thừa $y={{x}^{a}}$ trên khoảng $\left( 0;+\infty \right)$
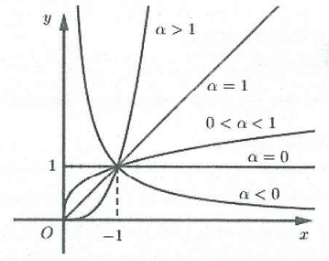Đồ thị hàm số $y={{x}^{\alpha }}$ luôn đi qua điểm $I\left( 1;1 \right).$
Lưu ý: Khi khảo sát hàm số lũy thừa với sỗ mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó. Chẳng hạn:
Hàm số: $y={{x}^{3}}$ $\left( x\in \mathbb{R} \right).$
Hàm số: $y={{x}^{-4}}$ $\left( x\ne 0 \right).$
Hàm số: $y={{x}^{\frac{1}{3}}}$ $\left( x>0 \right).$
