Giải PT Logarit bằng phương pháp đánh giá, hàm số có đáp án chi tiết
Kiến thức cần nhớ:
Hàm số $y=f\left( x \right)$ đồng biến (hoặc nghịch biến trên $\mathbb{R}$) thì phương trình $f\left( x \right)=f\left( {{x}_{0}} \right)\Leftrightarrow x={{x}_{0}}.$
Hàm số $f\left( t \right)$ đồng biến hoặc nghịch biến trên D (trong đó D là một khoảng, một đoạn, một nửa đoạn) thì với $u;v\in D$ ta có: $f\left( u \right)=f\left( v \right)\Leftrightarrow u=v.$
Một số bài tập, bài tập trắc nghiệm giải phương trình logarit
| Ví dụ 1: Giải các phương trình sau:
a) $\ln \left( \frac{2{{x}^{2}}+1}{{{x}^{2}}+x+1} \right)={{x}^{2}}-x.$ b) ${{\log }_{2}}\left( \frac{{{x}^{2}}+x+3}{2{{x}^{2}}+4x+5} \right)={{x}^{2}}+3x+2.$ |
Lời giải:
a) Điều kiện: $\frac{2{{x}^{2}}+1}{{{x}^{2}}+x+1}>0\Leftrightarrow x\in \mathbb{R}.$
Khi đó $PT\Leftrightarrow \ln \left( 2{{x}^{2}}+1 \right)-\ln \left( {{x}^{2}}+x+1 \right)=\left( 2{{x}^{2}}+1 \right)-\left( {{x}^{2}}+x+1 \right)$
$\Leftrightarrow \ln \left( 2{{x}^{2}}+1 \right)+2{{x}^{2}}+1=\ln \left( {{x}^{2}}+x+1 \right)+\left( {{x}^{2}}+x+1 \right)$
Xét hàm số $f\left( t \right)=\ln t+t\,\,\left( t>0 \right)$ ta có: $f’\left( t \right)=\frac{1}{t}+1>0\,\,\left( \forall t\in \mathbb{R} \right)$ suy ra hàm số$f\left( t \right)$đồng biến trên $\mathbb{R}$nên $f\left( 2{{x}^{2}}+1 \right)=f\left( {{x}^{2}}+x+1 \right)\Leftrightarrow 2{{x}^{2}}+1={{x}^{2}}+x+1\Leftrightarrow {{x}^{2}}=x\Leftrightarrow \left[ \begin{array} {} x=0 \\ {} x=1 \\ \end{array} \right..$
b) Đáp số: $x=-2;x=-1.$
| Ví dụ 2: Giải các phương trình sau:
a) ${{7}^{x}}-1=6{{\log }_{7}}\left( 6x+1 \right).$ b) ${{3}^{x}}+5x=4+4{{\log }_{3}}\left( 4-x \right).$ |
Lời giải:
a) Điều kiện: $x>-\frac{1}{6}$. Đặt $y={{\log }_{7}}\left( 6x+1 \right)$ ta có: $6x+1={{7}^{y}}$ và ${{7}^{x}}-1=6y$
Suy ra \(\left\{ \begin{align} & {{7}^{x}}=6y+1 \\ & {{7}^{y}}=6x+1 \\ \end{align} \right.\Rightarrow {{7}^{x}}-{{7}^{y}}=6y-6x\Leftrightarrow {{7}^{x}}+6x={{7}^{y}}+6y\)
Xét hàm số $f\left( t \right)={{7}^{t}}+6t\,\,\left( t\in \mathbb{R} \right)$ ta có: $f’\left( t \right)={{7}^{t}}\ln 7+6>0\,\,\left( \forall t\in \mathbb{R} \right)$ nên hàm số$f\left( t \right)$đồng biến trên $\mathbb{R}$ nên $f\left( x \right)=f\left( y \right)\Leftrightarrow x=y\Rightarrow x={{\log }_{7}}\left( 6x+1 \right)$
$\Leftrightarrow {{7}^{x}}=6x+1\Leftrightarrow g\left( x \right)={{7}^{x}}-6x-1=0$
Ta có: $g’\left( x \right)={{7}^{x}}\ln 7-6=0\Leftrightarrow x=\log \frac{6}{\ln 7}$
Suy ra BBT:
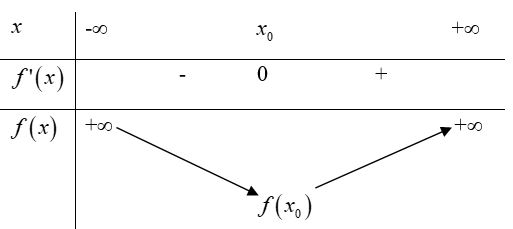
Do vậy PT $g\left( x \right)=0$ có nhiều nhất hai nghiệm. Mặt khác $g\left( 0 \right)=g\left( 1 \right)=0$
Vậy phương trình đã cho có hai nghiệm là $x=0;x=1.$
b) Điều kiện: $4-x>0$. Đặt $y={{\log }_{3}}\left( 4-x \right)\Rightarrow {{3}^{y}}=4-x$
Khi đó ${{3}^{x}}+4x=4-x+4{{\log }_{3}}\left( 4-x \right)={{3}^{y}}+4y\Rightarrow \left\{ \begin{array} {} {{3}^{y}}=4-x \\ {} {{3}^{x}}=4-y \\ \end{array} \right.\Rightarrow x=y$
Đáp số: $x=1.$
| Ví dụ 3: Giải các phương trình sau:
a) ${{\log }_{3}}\frac{{{x}^{2}}+x+3}{2{{x}^{2}}+4x+5}=7{{x}^{2}}+21x+14$ b) $2{{x}^{2}}-6x+2={{\log }_{2}}\frac{2x+1}{{{\left( x-1 \right)}^{2}}}$ |
Lời giải:
a) Ta có: ${{\log }_{3}}\frac{{{x}^{2}}+x+3}{2{{x}^{2}}+4x+5}=7\left( 2{{x}^{2}}+4x+5-{{x}^{2}}-x-3 \right)$.
$\Leftrightarrow {{\log }_{3}}\left( {{x}^{2}}+x+3 \right)+7\left( {{x}^{2}}+x+3 \right)={{\log }_{3}}\left( 2{{x}^{2}}+4x+5 \right)+7\left( 2{{x}^{2}}+4x+5 \right)$
Xét hàm số $f\left( t \right)={{\log }_{3}}t+t$ trên khoảng $\left( 0;+\infty \right)$ ta có: $f’\left( t \right)=\frac{1}{t\ln 3}+1>0\,\,\,\,\forall t\in \left( 0;+\infty \right)$
Do đó$f\left( {{x}^{2}}+x+3 \right)=f\left( 2{{x}^{2}}+4x+5 \right)\Leftrightarrow {{x}^{2}}+x+3=2{{x}^{2}}+4x+5\Leftrightarrow {{x}^{2}}+3x+2=0\Leftrightarrow \left[ \begin{array} {} x=-1 \\ {} x=2 \\ \end{array} \right.$
Đáp số: $x=-1;x=-2.$
b) Điều kiện: $\left\{ \begin{array} {} x\ne 1 \\ {} 2x+1>0 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} x>-\frac{1}{2} \\ {} x\ne 1 \\ \end{array} \right.$.
Khi đó: $PT\Leftrightarrow 2{{x}^{2}}-6x+2={{\log }_{2}}\left( 2x+1 \right)-{{\log }_{2}}{{\left( x-1 \right)}^{2}}$
$\begin{array} {} \Leftrightarrow 2\left( {{x}^{2}}-2x+1 \right)-2x={{\log }_{2}}\left( 2x+1 \right)-{{\log }_{2}}{{\left( x-1 \right)}^{2}} \\ {} \Leftrightarrow 2{{\left( x-1 \right)}^{2}}+{{\log }_{2}}{{\left( x-1 \right)}^{2}}=2x+1+{{\log }_{2}}\left( 2x+1 \right)-1 \\ {} \Leftrightarrow 2{{\left( x-1 \right)}^{2}}+{{\log }_{2}}{{\left( x-1 \right)}^{2}}=2\left( x+\frac{1}{2} \right)+{{\log }_{2}}\left( x+\frac{1}{2} \right) \\ \end{array}$
Xét hàm số $f\left( t \right)=2t+{{\log }_{2}}t\,\,\left( t\in \left( 0;+\infty \right) \right)$ ta có $f’\left( t \right)=2+\frac{1}{t\ln 2}>0\,\,\,\forall t\in \left( 0;+\infty \right)$
Do vậy $f\left[ {{\left( x-1 \right)}^{2}} \right]=f\left( x+\frac{1}{2} \right)\Leftrightarrow {{\left( x-1 \right)}^{2}}=x+\frac{1}{2}\Leftrightarrow x=\frac{3\pm \sqrt{7}}{2}\,\,\left( t/m \right).$
| Ví dụ 4: Số nghiệm của phương trình ${{\log }_{2}}\left( 3x+2 \right)+{{\log }_{3}}\left( x+1 \right)=4$ là:
A. 1. B. 2. C. 3. D. 4. |
Lời giải:
Điều kiện: $x>\frac{-2}{3}$. Xét hàm số: $f\left( x \right)={{\log }_{2}}\left( 3x+2 \right)+{{\log }_{3}}\left( x+1 \right)$ với $x>-\frac{3}{2},f\left( 2 \right)=4$
Ta có: $f’\left( x \right)=\frac{3}{\left( 3x+2 \right)\ln 2}+\frac{1}{\left( x+1 \right)\ln 3}>0\,\,\,\,\forall x>\frac{-2}{3}\Rightarrow f\left( x \right)$ đồng biến $\forall x>\frac{-2}{3}$
Do vậy $f\left( x \right)=f\left( 2 \right)\Leftrightarrow x=2$
Vậy $x=2$là nghiệm duy nhất của PT đã cho. Chọn A.
| Ví dụ 5: Số nghiệm của phương trình ${{\log }_{2}}\frac{2x-1}{{{\left( x-1 \right)}^{2}}}=3{{x}^{2}}-8x+5$ là:
A. 1. B. 2. C. 3. D. 4. |
Lời giải:
Điều kiện: $\frac{1}{2}0 \right)$ đồng biến trên khoảng $\left( 0;+\infty \right)$
Do đó $f\left( 2x-1 \right)=f\left( 3{{x}^{2}}-6x+3 \right)\Leftrightarrow 2x-1=3{{x}^{2}}-6x+3\Leftrightarrow 3{{x}^{2}}-8x+4=0$
$\Leftrightarrow \left[ \begin{array} {} x=2 \\ {} x=\frac{2}{3} \\ \end{array} \right.\Rightarrow $phương trình có hai nghiệm. Chọn B.
| Ví dụ 6: Tập nghiệm của phương trình: ${{\log }_{2}}\frac{{{x}^{2}}+x+2}{2{{x}^{2}}-3x+5}={{x}^{2}}-4x+3$ là:
A. $\left\{ -1;-3 \right\}$. B. $\left\{ 1;-3 \right\}$. C. $\left\{ -1;3 \right\}$. D.$\left\{ 1;3 \right\}$. |
Lời giải:
Phương trình $\Leftrightarrow {{\log }_{2}}\left( {{x}^{2}}+x+2 \right)-{{\log }_{2}}\left( 2{{x}^{2}}-3x+5 \right)=\left( 2{{x}^{2}}-3x+5 \right)-\left( {{x}^{2}}+x+2 \right)$
$\Leftrightarrow {{\log }_{2}}\left( {{x}^{2}}+x+2 \right)+\left( {{x}^{2}}+x+2 \right)={{\log }_{2}}\left( 2{{x}^{2}}-3x+5 \right)+\left( 2{{x}^{2}}-3x+5 \right)$
Xét hàm số $f\left( t \right)={{\log }_{2}}t+t\,,\,\,t>0.$ Ta có: $f’\left( t \right)=\frac{1}{t\ln 2}+1>0\,\,\,\forall t>0\Rightarrow $Hàm $f$ đồng biến trên $\left( 0;+\infty \right).$
Do đó: $f\left( {{x}^{2}}+x+2 \right)=f\left( 2{{x}^{2}}-3x+5 \right)\Leftrightarrow {{x}^{2}}+x+2=2{{x}^{2}}-3x+5\Leftrightarrow {{x}^{2}}-4x+3=0\Leftrightarrow \left[ \begin{array} {} x=1 \\ {} x=3 \\ \end{array} \right..$
Vậy tập nghiệm của phương trình đã cho là: $\left\{ 1;3 \right\}$. Chọn D.
