Công thức ứng dụng tích phân tính thể tích – lý thuyết và các dạng bài tập
Tính thể tích vật thể
Cắt một vật thể $\left( H \right)$ bởi hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ vuông góc với trục $Ox$ lần lượt tại $x=a;\,\,x=b\,\,\left( a<b \right).$ Một mặt phẳng tuỳ ý vuông góc với $Ox$ tại điểm $x$ ($a\le x\le b$) cắt $\left( H \right)$ theo thiết diện là $S\left( x \right)$ (hình vẽ). Giả sử $S\left( x \right)$ liên tục trên đoạn $\left[ a;b \right].$
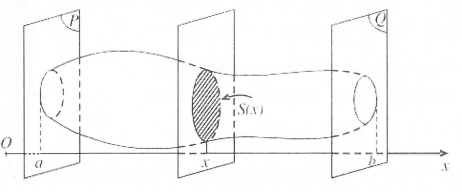
Khi đó thể tích $V$ của vật thể $\left( H \right)$ giới hạn bởi hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ được tính bởi công thức:
$V=\int_{a}^{b}{S\left( x \right)dx}.$
Tính thể tích vật tròn xoay sinh bởi diện tích S quay quanh trục Ox
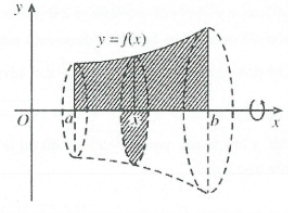
Giả sử một hình thang cong giới hạn bởi đồ thị hàm số $y=f\left( x \right)$, trục $Ox$ và hai đường thẳng $x=a$ và $x=b\,\,\,\,\left( a<b \right)$ quay quanh trục $Ox$ tạo thành một khối tròn xoay (hình vẽ). Khi đó ta có thể tích vật thể là: $V=\int_{a}^{b}{S\left( x \right)dx}$
Mặt khác tại điểm $x$ ta có $S\left( x \right)$ là một hình tròn có bán kính $R=f\left( x \right)$
$\Rightarrow S\,\left( x \right)=\pi {{R}^{2}}=\pi {{f}^{2}}\left( x \right)$. Vậy ${{V}_{Ox}}=\pi \int_{a}^{b}{{{f}^{2}}\left( x \right)dx}.$
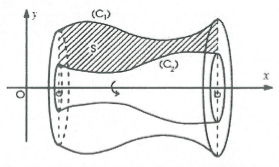
Trong trường hợp $S\left( x \right)$ giới hạn bởi hai đồ thị hàm số $y=f\left( x \right)$ và $y=g\left( x \right)$ ta được khối tròn xoay có thể tích là:
${{V}_{Ox}}=\pi \int_{a}^{b}{\left| {{f}^{2}}\left( x \right)-{{g}^{2}}\left( x \right) \right|dx}.$
Chú ý: Khi bài toán không cho hai đường thẳng giới hạn $x=a$ và $x=b$ thì ta giải phương trình $f\left( x \right)=g\left( x \right)$ để tìm cận của tích phân, trong đó $x=a$ là nghiệm nhỏ nhất và $x=b$ là nghiệm lớn nhất của phương trình.
Tính thể tích vật tròn xoay sinh bởi diện tích S quay quanh trục Oy
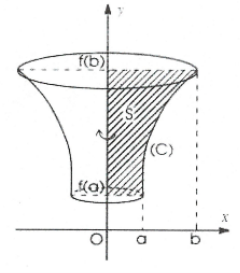
Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi đồ thị hàm số $y=f\left( x \right)$ trục $Oy$ và hai đường thẳng $y=f\left( a \right);\,\,y=f\left( b \right).$
– Bước 1: Biến đổi $y=f\left( x \right)$ về dạng $x={{f}_{1}}\left( y \right).$
– Bước 2: Khi đó ${{V}_{Oy}}=\pi \int\limits_{f\left( a \right)}^{f\left( b \right)}{f_{1}^{2}}\left( y \right)dy.$
Tương tự: Trong trường hợp ${{V}_{Oy}}$ sinh ra bởi diện tích hình phẳng của hai đồ thị hàm số $y=f\left( x \right);\,\,y=g\left( x \right)$ và hai đường thẳng $y=m {} \,;\,\,y=n$ ta có ${{V}_{Oy}}=\pi \int\limits_{m}^{n}{\left| f_{1}^{2}\left( y \right)-g_{1}^{2}\left( y \right) \right|}\,dy.$
Chú ý: Khi quay diện tích hình phẳng $S$ quanh trục $Ox$ ta được khối tròn xoay có thể tích ${{V}_{Ox}}$. Khi quay quanh trục $Oy$ ta được khối tròn xoay có thể tích ${{V}_{Oy}}.$
Hầu như ${{V}_{Ox}}$ không bằng ${{V}_{Oy}}$. Chúng chỉ bằng nhau trong một số trường hợp đặc biệt.
Ứng dụng tính thể tích khối cầu, khối chỏm cầu và một số hình đặc biệt
– Thể tích của khối cầu
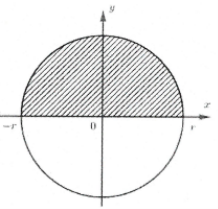
Trong hệ tọa độ Oxy cho nửa đường tròn có phương trình: $\left( P \right):{{x}^{2}}+{{y}^{2}}={{r}^{2}}$ với $r>0;\,\,y\ge 0$ (hình vẽ). Quay nửa hình tròn đó quanh trục hoành ta được một mặt cầu có bán kính $r.$
Thể tích của mặt cầu này là: $V=\frac{4}{3}\pi {{r}^{3}}\,\,\left( vtt \right)$.
Thật vậy: Ta có ${{x}^{2}}+{{y}^{2}}={{r}^{2}}\Leftrightarrow y=\pm \sqrt{{{r}^{2}}-{{x}^{2}}}$
Với $y\ge 0$ ta có: $y=\sqrt{{{r}^{2}}-{{x}^{2}}}$có đồ thị là nửa đường tròn phía trên trục hoành.
Khi đó thể tích khối cầu $V=\pi \int\limits_{-r}^{r}{{{\left( \sqrt{{{r}^{2}}-{{x}^{2}}} \right)}^{2}}dx}=2\pi \int\limits_{0}^{r}{\left( {{r}^{2}}-{{x}^{2}} \right)dx=\left. 2\pi \left( {{r}^{2}}x-\frac{{{x}^{3}}}{3} \right) \right|}_{0}^{r}$
$=2\pi \left( {{r}^{3}}-\frac{{{r}^{3}}}{3} \right)=\frac{4\pi {{r}^{3}}}{3}\,\,\left( vtt \right)$
