Công thức tỷ số thể tích, định lý simson đầy đủ các kỹ thuật giải nhanh
Chú thích ${{V}_{1}}=$Thể tích cũ, ${{V}_{2}}=$Thể tích mới (dùng cho kỹ thuật chuyển đỉnh và đáy).
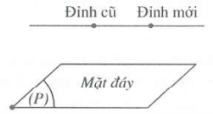
Kỹ thuật đổi đỉnh (đáy không đổi)
- Song song với đáy
${{V}_{1}}={{V}_{2}}=\frac{1}{3}Bh.$
- Cắt đáy
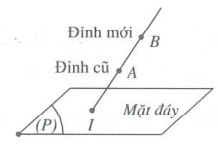
$\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{\frac{1}{3}.d\left( A;\left( P \right) \right).{{S}_{}}}{\frac{1}{3}.d\left( B;\left( P \right) \right).{{S}_{}}}=\frac{d\left( A;\left( P \right) \right)}{d\left( B;\left( P \right) \right)}=\frac{IB}{IA}.$
Kỹ thuật chuyển đáy (đường cao không đổi)
$$;với ${{S}_{1}}$ là diện tích đáy cũ; ${{S}_{2}}$ là diện tích đáy mới
Chú ý:
- Đưa hai khối đa diện về cùng một đỉnh; hai đáy mới và cũ nằm trong cùng một mặt phẳng (thường thì đáy cũ chứa đáy mới). Áp dụng công thức tính diện tích của đa giác để so sánh tỉ số giữa đáy cũ và đáy mới.
- Nếu tăng (hoặc giảm) mỗi cạnh của đa giác (tam giác, tứ giác), k lần thì diện tích đa giác sẽ tăng (hoặc giảm) ${{k}^{2}}$ lần.
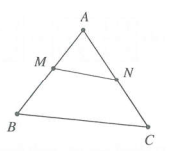
- Tỉ số đa giác hay gặp là tỉ số diện tích của hai tam giác.
$\frac{{{S}_{\Delta AMN}}}{{{S}_{\Delta ABC}}}=\frac{\frac{1}{2}.AM.AN.\sin A}{\frac{1}{2}.AB.AC.\sin A}=\frac{AM}{AB}.\frac{AN}{AC}.$
Tỉ số thể tích của khối chóp
- Tỉ số thể tích của khối chóp tam giác
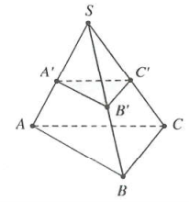
Công thức: $$
Lưu ý: Công thức chỉ áp dụng với khối chóp có đáy là tam giác nên trong nhiều trường hợp ta cần chia nhỏ các khối đa diện thành các hình chóp tam giác khác nhau rồi mới áp dụng.
Tỉ số thể tích của khối chóp tứ giác
- Trường hợp đặc biệt: Cho hình chóp $S.ABCD$có đáy $ABCD$ (hoặc đa giác bất kỳ), mặt phẳng $\left( P \right)$ song song với đáy cắt các cạnh bên $SA,SB,SC,SD$lần lượt tại ${A}’,{B}’,{C}’,{D}’$.
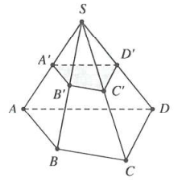
Khi đó $$; với $\frac{S{A}’}{SA}.\frac{S{B}’}{SB}.\frac{S{C}’}{SC}=\frac{S{D}’}{SD}=k$.
Chú ý: Công thức trên đúng với đáy n giác.
Trường hợp đáy là hình bình hành (hay gặp)
Bài toán: Cho hình chóp $S.ABCD$có đáy $ABCD$ là hình bình hành. Mặt phẳng $\left( P \right)$ cắt các cạnh $SA,SB,SC,SD$lần lượt tại ${A}’,{B}’,{C}’,{D}’$sao cho $\frac{S{A}’}{SA}=x;\frac{S{B}’}{SB}=y;\frac{S{C}’}{SC}=z;\frac{S{D}’}{SD}=t.$
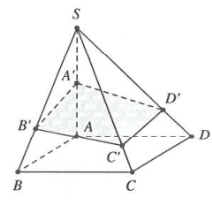
Khi đó $$ và $$
Tỉ số thể tích của khối lăng trụ
- Lăng trụ tam giác
þ Kết quả 1:
Gọi V là thể tích khối lăng trụ, ${{V}_{1}}$ là thể tích khối chóp tạo thành từ 4 trong 6 đỉnh của lăng trụ, ${{V}_{2}}$ là thể tích khối chóp tạo thành từ 5 trong 6 đỉnh của lăng trụ. Khi đó: $$
Bài tập: Hình lăng trụ $ABC.{A}'{B}'{C}’\xrightarrow{{}}{{V}_{{A}'{B}’BC}}=\frac{1}{3}{{V}_{ABC.{A}'{B}'{C}’}};{{V}_{{A}'{B}’ABC}}=\frac{2}{3}{{V}_{ABC.{A}'{B}'{C}’}}$
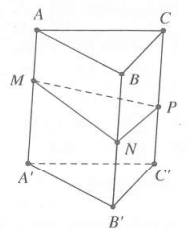
þ Kết quả 2:
Cho hình lăng trụ tam giác $ABC.{A}'{B}'{C}’$. Mặt phẳng $\left( \alpha \right)$cắt các đường thẳng $A{A}’,B{B}’,C{C}’$lần lượt tại $M,N,P$ (tham khảo hình vẽ bên). Tính tỉ số $\frac{{{V}_{ABC.MNP}}}{{{V}_{ABC.{A}'{B}'{C}’}}}$.
HD: Ta có ${{V}_{ABC.MNP}}={{V}_{M.ABC}}+{{V}_{A.BNPC}}$
Lại có ${{V}_{M.ABC}}=\frac{1}{3}.d\left( M;\left( ABC \right) \right).{{S}_{\Delta ABC}}=\frac{1}{3}.\frac{AM}{A{A}’}.d\left( {A}’;\left( ABC \right) \right).{{S}_{\Delta ABC}}$
$=\frac{1}{3}.\frac{AM}{A{A}’}.{{V}_{ABC.{A}'{B}'{C}’}}\xrightarrow[{}]{}{{V}_{M.ABC}}=\frac{1}{3}.\frac{AM}{A{A}’}.{{V}_{ABC.{A}'{B}'{C}’}}$
Và ${{S}_{BNPC}}=\frac{h}{2}.\left( BN+CP \right);$${{S}_{BC{C}'{B}’}}=\frac{h}{2}.\left( B{B}’+C{C}’ \right)=h.B{B}’$
$\Rightarrow \frac{{{S}_{BNPC}}}{{{S}_{BC{C}'{B}’}}}=\frac{\frac{h}{2}.\left( BN+CP \right)}{h.B{B}’}=\frac{1}{2}\left( \frac{BN+CP}{B{B}’} \right)=\frac{1}{2}\left( \frac{BN}{B{B}’}+\frac{CP}{C{C}’} \right).$
Suy ra ${{V}_{A.BNPC}}=\frac{1}{3}.d\left( A;\left( BC{C}'{B}’ \right) \right).{{S}_{BNPC}}$
$=\frac{1}{3}.d\left( A;\left( BC{C}'{B}’ \right) \right).\frac{1}{2}\left( \frac{BN}{B{B}’}+\frac{CP}{C{C}’} \right).{{S}_{BC{C}'{B}’}}=\frac{1}{2}\left( \frac{BN}{B{B}’}+\frac{CP}{C{C}’} \right).{{V}_{A.BC{C}'{B}’}}$
Mà ${{V}_{A.BC{C}'{B}’}}=\frac{2}{3}{{V}_{ABC.{A}'{B}'{C}’}}\Rightarrow {{V}_{A.BNPC}}=\frac{1}{3}.\left( \frac{BN}{B{B}’}+\frac{CP}{C{C}’} \right).{{V}_{ABC.{A}'{B}'{C}’}}$
Vậy ${{V}_{ABC.MNP}}=\frac{1}{3}.\frac{AM}{A{A}’}.{{V}_{ABC.{A}'{B}'{C}’}}+\frac{1}{3}.\left( \frac{BN}{B{B}’}+\frac{CP}{C{C}’} \right).{{V}_{ABC.{A}'{B}'{C}’}}\Rightarrow \frac{{{V}_{ABC.MNP}}}{{{V}_{ABC.{A}'{B}'{C}’}}}=\frac{1}{3}\left( \frac{AM}{A{A}’}+\frac{BN}{B{B}’}+\frac{CP}{C{C}’} \right)$
Công thức tính nhanh $$
- Khối hộp
þ Kết quả 1:
Gọi V là thể tích khối hộp, ${{V}_{1}}$ là thể tích khối chóp tạo thành từ 4 trong 8 đỉnh của khối hộp gồm hai đường chéo của hai mặt song song, ${{V}_{2}}$ là thể tích khối chóp tạo thành từ 4 trong 8 đỉnh của khối hộp ở các trường hợp còn lại. Khi đó: $$
Bài tập: Hình hộp $ABCD.{A}'{B}'{C}'{D}’\xrightarrow{{}}{{V}_{{A}’C’BD}}=\frac{1}{3}{{V}_{ABCD.{A}'{B}'{C}'{D}’}};{{V}_{{A}'{C}'{D}’D}}=\frac{1}{6}{{V}_{ABCD.{A}'{B}'{C}'{D}’}}$
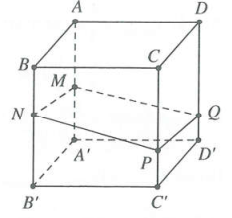
þ Kết quả 2:
Cho hình lăng trụ tam giác $ABCD.{A}'{B}'{C}'{D}’$. Mặt phẳng $\left( \alpha \right)$cắt các đường thẳng $A{A}’,B{B}’,C{C}’,D{D}’$lần lượt tại $M,N,P,Q$ (tham khảo hình vẽ bên).
Chứng minh rằng $\frac{AM}{A{A}’}+\frac{CP}{C{C}’}=\frac{BN}{B{B}’}+\frac{DQ}{D{D}’}$
và $\frac{{{V}_{ABCD.MNPQ}}}{{{V}_{ABCD.{A}'{B}'{C}'{D}’}}}=\frac{1}{2}\left( \frac{AM}{A{A}’}+\frac{CP}{C{C}’} \right)=\frac{1}{2}\left( \frac{BN}{B{B}’}+\frac{DQ}{D{D}’} \right)$
- Chứng minh $\frac{AM}{A{A}’}+\frac{CP}{C{C}’}=\frac{BN}{B{B}’}+\frac{DQ}{D{D}’}$
Gọi I là tâm hình vuông ABCD; ${I}’$ là tâm hình vuông ${A}'{B}'{C}'{D}’$.
Ta có: $\frac{AM}{A{A}’}+\frac{CP}{C{C}’}=\frac{AM+PC}{A{A}’}=\frac{2OI}{A{A}’};$
$\frac{BN}{B{B}’}+\frac{DQ}{D{D}’}=\frac{BN+DQ}{B{B}’}=\frac{2O{I}’}{B{B}’}\Rightarrow \frac{AM}{A{A}’}+\frac{CP}{C{C}’}=\frac{BN}{B{B}’}+\frac{DQ}{D{D}’}.$
- Chứng minh $\frac{{{V}_{ABCD.MNPQ}}}{{{V}_{ABCD.{A}'{B}'{C}'{D}’}}}=\frac{1}{2}\left( \frac{AM}{A{A}’}+\frac{CP}{C{C}’} \right)=\frac{1}{2}\left( \frac{BN}{B{B}’}+\frac{DQ}{D{D}’} \right)$
Chia khối đa diện $ABCD.MNPQ$thành hai khối đa diện $ABC.MNP$ và $ACD.MPQ$;
Làm tương tự với thể tích khối lăng trụ tam giác;
Cộng thể tích hai khối đa diện $\Rightarrow \frac{{{V}_{ABC.MNP}}}{{{V}_{ABC.{A}'{B}'{C}’}}}=\frac{1}{4}\left( \frac{AM}{A{A}’}+\frac{CP}{C{C}’}+\frac{BN}{B{B}’}+\frac{DQ}{D{D}’} \right)$
Mà $\frac{AM}{A{A}’}+\frac{CP}{C{C}’}=\frac{BN}{B{B}’}+\frac{DQ}{D{D}’}\Rightarrow \frac{{{V}_{ABCD.MNPQ}}}{{{V}_{ABCD.{A}'{B}'{C}'{D}’}}}=\frac{1}{2}\left( \frac{AM}{A{A}’}+\frac{CP}{C{C}’} \right)=\frac{1}{2}\left( \frac{BN}{B{B}’}+\frac{DQ}{D{D}’} \right)$
Công thức tính nhanh
$$