Bài tập trắc nghiệm Tỉ số thể tích của khối chóp có đáp án chi tiết
Dưới đây là một số bài tính thể tích sử dụng tỷ số thể tích có đáp án
| Bài tập 1: Cho hình chóp $S.ABC$ có thể tích $V=18.$ Gọi M là trung điểm của SA, E là điểm đối xứng với B qua C. Gọi N là giao điểm của hai đường thẳng SB và ME.
a) Tính thể tích khối chóp MABE b) Tính thể tích khối chóp AMNBC c) Tính thể tích khối chóp SANE |
Lời giải chi tiết
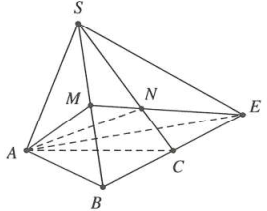
Vì E đối xứng với B qua C $\Rightarrow $ C là trung điểm của BE.
Mà M là trung điểm của SB. $SC\cap ME=N$
Suy ra N là trọng tâm $\Delta SBE\xrightarrow{{}}\frac{SN}{SC}=\frac{2}{3}$.
a) Ta có: ${{S}_{\Delta SBE}}=\frac{1}{2}{{d}_{A\to BC}}.BE=2\frac{1}{2}{{d}_{A\to BC}}.BC=2.{{S}_{ABC}}$
Và $\frac{d\left( S;\left( ABC \right) \right)}{d\left( M;\left( ABC \right) \right)}=\frac{SB}{BM}\Rightarrow d\left( M;\left( ABC \right) \right)=\frac{1}{2}d\left( S;\left( ABC \right) \right)$
Khi đó ${{V}_{M.ABE}}=\frac{1}{3}d\left( M;\left( ABC \right) \right).{{S}_{\Delta SBE}}$
$=\frac{1}{2}.2.\frac{1}{3}d\left( M;\left( ABC \right) \right).{{S}_{\Delta ABC}}={{V}_{S.ABC}}=18.$
b) Ta có $\frac{{{V}_{S.AMN}}}{{{V}_{S.ABC}}}=\frac{SM}{SB}.\frac{SN}{SC}=\frac{1}{2}.\frac{2}{3}=\frac{1}{3}\Rightarrow {{V}_{S.AMN}}=\frac{1}{3}{{V}_{S.ABC}}$
Lại có ${{V}_{S.ABC}}={{V}_{S.AMN}}+{{V}_{AMNBC}}\xrightarrow[{}]{}{{V}_{AMNBC}}={{V}_{S.ABC}}-{{V}_{S.AMN}}=\frac{2}{3}{{V}_{S.ABC}}=\frac{2}{3}.18=12$
c) Ta có ${{V}_{S.ANE}}={{V}_{S.AME}}-{{V}_{S.AMN}}={{V}_{S.AME}}-\frac{1}{3}{{V}_{S.ABC}}$
Lại có $\frac{{{V}_{S.AME}}}{{{V}_{S.ABE}}}=\frac{SM}{SB}=\frac{1}{2}\xrightarrow{{}}{{V}_{S.AME}}=\frac{1}{2}{{V}_{S.ABE}}=\frac{1}{2}.2{{V}_{S.ABC}}={{V}_{S.ABC}}$
Do đó ${{V}_{S.ANE}}={{V}_{S.ABC}}-\frac{1}{3}{{V}_{S.ABC}}=\frac{2}{3}{{V}_{S.ABC}}=\frac{2}{3}.18=12$
| Bài tập 2: Cho hình chóp đều $S.ABC$ có đáy cạnh bằng a, cạnh bên bằng 2a.
a) Gọi M, N lần lượt thuộc AB, AC sao cho $2AM=AB,AN=2NC.$ Tính ${{V}_{S.MBCN}}$ b) Mặt phẳng $\left( P \right)$ đi qua trọng tâm của tam giác ABC, song song với SA và BC, biết $\left( P \right)$ cắt SB, SC lần lượt tại P, Q. Tính thể tích khối chóp MPQCB |
Lời giải chi tiết
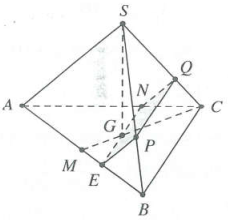
Gọi G là trọng tâm tam giác $ABC\Rightarrow SG\bot \left( ABC \right)$.
Tam giác SAG vuông tại G, có
$SG=\sqrt{S{{A}^{2}}-A{{G}^{2}}}=\sqrt{{{\left( 2a \right)}^{2}}-{{\left( \frac{a\sqrt{3}}{3} \right)}^{2}}}=\frac{a\sqrt{33}}{3}.$
$\Rightarrow $ Thể tích khối chóp $S.ABC$ là ${{V}_{S.ABC}}=\frac{1}{3}.SG.{{S}_{\Delta ABC}}=\frac{{{a}^{3}}\sqrt{11}}{12}$
a) Ta có $\frac{{{S}_{\Delta AMN}}}{{{S}_{\Delta ABC}}}=\frac{AM}{AB}.\frac{AN}{AC}=\frac{1}{2}.\frac{2}{3}=\frac{1}{3}\Rightarrow \frac{{{V}_{S.AMN}}}{{{V}_{S.ABC}}}=\frac{1}{3}$
Mà ${{V}_{S.ABC}}={{V}_{S.AMN}}+{{V}_{S.MBCN}}\xrightarrow[{}]{}{{V}_{S.MBCN}}=\frac{2}{3}{{V}_{S.ABC}}=\frac{{{a}^{3}}\sqrt{11}}{18}$
b) Qua G kẻ đường thẳng song song với BC, cắt AB, AC lần lượt tại E, N. Tương tự, từ E, N kẻ các đường thẳng song song với BC cắt SB, SC lần lượt tại P, Q.
Dễ dàng chứng minh được $\frac{SP}{SB}=\frac{SQ}{SC}=\frac{AN}{AC}=\frac{2}{3}.$
Ta có: ${{V}_{MPQCB}}=\frac{1}{2}{{V}_{A.PQCB}}=\frac{1}{2}\left( {{V}_{S.ABC}}-{{V}_{S.APQ}} \right)=\frac{1}{2}\left( {{V}_{S.ABC}}-\frac{SP}{SB}.\frac{SQ}{SC}.{{V}_{S.ABC}} \right)=\frac{5}{18}{{V}_{S.ABC}}.$
Vậy thể tích cần tìm là ${{V}_{MPQCB}}=\frac{5}{18}.\frac{{{a}^{3}}\sqrt{11}}{12}=\frac{5\sqrt{11}}{216}{{a}^{3}}$.
| Bài tập 3: Cho hình chóp $S.ABC$ có đáy ABCD là hình vuông cạnh $a\sqrt{2}$, cạnh bên SA vuông góc với đáy. Góc giữa hai mặt phẳng $\left( SBD \right)$ và $\left( ABCD \right)$bằng $45{}^\circ $.
a) Gọi M, N, P lần lượt là trung điểm của SA, SB, AB. Tính ${{V}_{MNPD}}$. b) Gọi H là hình chiếu của A trên SD; E là trung điểm của BC. Nối AC cắt DE tại F. Tính thể tích các khối đa diện MHCD, HFCD. |
Lời giải chi tiết
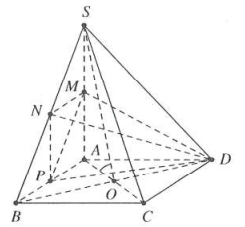
Gọi O là tâm hình vuông ABCD $\Rightarrow \widehat{\left( SBD \right);\left( ABCD \right)}=\widehat{SOA}=45{}^\circ $
Suy ra$SA=OA=\frac{AC}{2}=a\xrightarrow[{}]{}{{V}_{S.ABCD}}=\frac{1}{3}.SA.{{S}_{ABCD}}=\frac{a}{3}.{{\left( a\sqrt{2} \right)}^{2}}=\frac{2{{a}^{3}}}{3}.$
a) Ta có ${{S}_{\Delta MNP}}={{S}_{\Delta SAB}}-{{S}_{\Delta SMN}}-{{S}_{\Delta AMP}}-{{S}_{\Delta BPN}}$
$={{S}_{\Delta SAB}}-\frac{1}{4}{{S}_{\Delta SAB}}-\frac{1}{4}{{S}_{\Delta SAB}}-\frac{1}{4}{{S}_{\Delta SAB}}=\frac{1}{4}{{S}_{\Delta SAB}}.$
Lại có ${{V}_{MNPD}}={{V}_{D.MNP}}=\frac{1}{3}d\left( D;\left( SAB \right) \right).{{S}_{\Delta MNP}}=\frac{1}{4}{{V}_{D.SAB}}$
$=\frac{1}{4}{{V}_{S.ABD}}=\frac{1}{4}.\frac{{{S}_{\Delta ABD}}}{{{S}_{ABCD}}}.{{V}_{S.ABCD}}=\frac{1}{8}{{V}_{S.ABCD}}=\frac{1}{8}.\frac{2{{a}^{3}}}{3}=\frac{{{a}^{3}}}{12}.$
b) Xét $\Delta SAD$ vuông tại A, đường cao AH $\Rightarrow \frac{SH}{SD}={{\left( \frac{SA}{SD} \right)}^{2}}=\frac{1}{3}.$
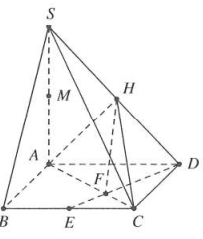
Tính thể tích khối chóp MHCD.
Ta có $\frac{{{S}_{\Delta HCD}}}{{{S}_{\Delta SCD}}}=\frac{HD}{SD}=\frac{1}{3}\Rightarrow {{S}_{\Delta HCD}}=\frac{1}{3}{{S}_{\Delta SCD}}$
$\Rightarrow {{V}_{M.HCD}}=\frac{1}{3}.d\left( M;\left( SCD \right) \right).{{S}_{\Delta HCD}}=\frac{1}{6}.\frac{1}{3}.d\left( A;\left( SCD \right) \right).{{S}_{\Delta SCD}}$
$=\frac{1}{6}{{V}_{A.SCD}}=\frac{1}{6}{{V}_{S.ACD}}=\frac{1}{6}.\frac{1}{2}{{V}_{S.ABCD}}=\frac{1}{12}.{{V}_{S.ABCD}}=\frac{{{a}^{3}}}{18}.$
Tính thể tích khối chóp HFCD.
Vì $EC//AD\Rightarrow \frac{EC}{AD}=\frac{CF}{AC}=\frac{EF}{FD}=\frac{1}{2}\Rightarrow \frac{DF}{DE}=\frac{2}{3}.$
Cách 1. Ta có ${{V}_{H.FCD}}=\frac{1}{3}.d\left( H;\left( ABCD \right) \right).{{S}_{\Delta FCD}}$ mà $\frac{d\left( H;\left( ABCD \right) \right)}{d\left( S;\left( ABCD \right) \right)}=\frac{HD}{SD}=\frac{2}{3}.$
Và $\frac{{{S}_{\Delta FCD}}}{{{S}_{\Delta ECD}}}=\frac{DF}{DE}=\frac{2}{3}\xrightarrow{{}}{{V}_{H.FCD}}=\frac{4}{9}.{{V}_{S.ECD}}=\frac{4}{9}.\frac{1}{4}{{V}_{S.ABCD}}=\frac{1}{9}{{V}_{S.ABCD}}=\frac{2{{a}^{3}}}{27}.$
Cách 2. Ta có ${{V}_{H.FCD}}={{V}_{F.HCD}}=\frac{1}{3}.d\left( F;\left( SCD \right) \right).{{S}_{\Delta HCD}}=\frac{1}{3}.\frac{1}{3}d\left( A;\left( SCD \right) \right).\frac{2}{3}{{S}_{\Delta SCD}}$
$=\frac{2}{9}{{V}_{A.SCD}}=\frac{2}{9}{{V}_{S.ACD}}=\frac{2}{9}.\frac{1}{2}{{V}_{S.ABCD}}=\frac{1}{9}{{V}_{S.ABCD}}=\frac{2{{a}^{3}}}{27}.$
| Bài tập 4: Cho tứ diện ABCD có thể tích V. Gọi ${V}’$ là thể tích của khối tứ diện có các đỉnh là trọng tâm của các mặt của khối tứ diện ABCD. Tính tỉ số $\frac{{{V}’}}{V}$.
A. $\frac{{{V}’}}{V}=\frac{8}{27}.$ B. $\frac{{{V}’}}{V}=\frac{23}{27}.$ C. $\frac{{{V}’}}{V}=\frac{1}{27}.$ D. $\frac{{{V}’}}{V}=\frac{4}{27}.$ |
Lời giải chi tiết
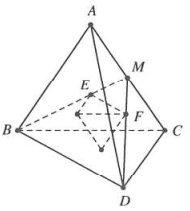
Gọi M là trung điểm AC; E, F lần lượt là trọng tâm của tam giác ABC, ACD. Trong tam giác MBD có $EF=\frac{1}{3}BD.$
Tương tự ta có các cạnh còn lại của tứ diện mới sinh ra bằng $\frac{1}{3}$ cạnh của tứ diện ban đầu. Do đó $\frac{{{V}’}}{V}={{\left( \frac{1}{3} \right)}^{3}}=\frac{1}{27}.$ Chọn C.
| Bài tập 5: Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc và $AB=6a,AC=9a,AD=3a.$ Gọi M, N, P lần lượt là trọng tâm của các tam giác ABC, ACD, ADB. Tính thể tích V của khối tứ diện AMNP.
A. $V=8{{a}^{2}}.$ B. $V=4{{a}^{2}}.$ C. $V=6{{a}^{2}}.$ D. $V=2{{a}^{2}}.$ |
Lời giải chi tiết
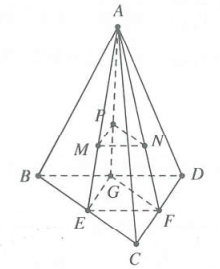
Ta có: ${{V}_{ABCD}}=\frac{1}{6}AB.AC.AD=27{{a}^{3}}.$
Gọi E, F, G lần lượt là trung điểm của BC, CD, DB.
Suy ra ${{V}_{AEFG}}=\frac{1}{4}{{V}_{ABCD}}=\frac{27}{4}{{a}^{3}}.$
Do M, N, P là trọng tâm của các tam giác ABC, ACD, ADB.
Nên ta có: $\frac{AM}{AE}=\frac{AN}{AF}=\frac{AP}{AG}=\frac{2}{3}.$
Lại có: $\frac{{{V}_{A.MNP}}}{{{V}_{A.EFG}}}=\frac{AM}{AE}.\frac{AN}{AF}.\frac{AP}{AG}=\frac{8}{27}.$
$\xrightarrow{{}}{{V}_{A.MNP}}=\frac{8}{27}.{{V}_{A.EFG}}=2{{a}^{3}}.$ Chọn D.
| Bài tập 6: Cho hình chóp S.ABCD có chiều cao bằng 9, diện tích đáy bằng 5. Gọi M là trung điểm của cạnh SB và N thuộc cạnh SC sao cho $NS=2NC.$ Tính thể tích V của khối chóp A.BMNC.
A. $V=15.$ B. $V=5.$ C. $V=10.$ D. $V=6.$ |
Lời giải chi tiết
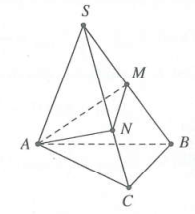
Từ giả thiết, ta có $\frac{SN}{SC}=\frac{2}{3}$ và $\frac{SM}{SB}=\frac{1}{2}$.
Thể tích khối chóp ${{V}_{S.ABC}}=\frac{1}{3}.9.5=15$
Ta có $\frac{{{V}_{S.AMN}}}{{{V}_{S.ABC}}}=\frac{SM}{SB}.\frac{SN}{SC}=\frac{1}{3}\Rightarrow {{V}_{ABMNC}}=\frac{2}{3}{{V}_{S.ABC}}=10.$ Chọn C.
| Bài tập 7: Cho hình chóp S.ABC có $SA=3,SB=4,SC=5$ và $\widehat{ASB}=\widehat{BSC}=\widehat{CSA}=60{}^\circ .$ Tính thể tích V của khối chóp đã cho.
A. $V=5\sqrt{2}.$ B. $V=5\sqrt{3}.$ C. $V=10.$ D. $V=15.$ |
Lời giải chi tiết
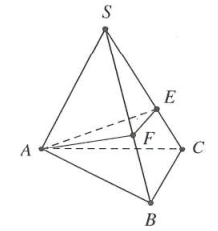
Trên SB, SC lần lượt lấy các điểm E, F sao cho $SE=SF=3.$.
Khi đó S.AEF là khối tứ diện đều có cạnh $a=3$.
Suy ra thể tích khối chóp S.AEF là ${{V}_{S.AEF}}=\frac{{{a}^{3}}\sqrt{2}}{12}=\frac{9\sqrt{2}}{4}.$
Ta có: $\frac{{{V}_{S.AEF}}}{{{V}_{S.ABC}}}=\frac{SE}{SB}.\frac{SF}{SC}=\frac{3}{4}.\frac{3}{5}=\frac{9}{20}.$
$\xrightarrow{{}}{{V}_{S.ABC}}=\frac{20}{9}.{{V}_{S.AEF}}=5\sqrt{2}.$ Chọn A.
| Bài tập 8: Cho tứ diện đều cạnh ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng $\left( MNE \right)$ chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V A. $V=\frac{7\sqrt{2}{{a}^{3}}}{216}$ B. $V=\frac{11\sqrt{2}{{a}^{3}}}{216}$ C. $V=\frac{13\sqrt{2}{{a}^{3}}}{216}$ D. $V=\frac{\sqrt{2}{{a}^{3}}}{18}$ |
Lời giải chi tiết
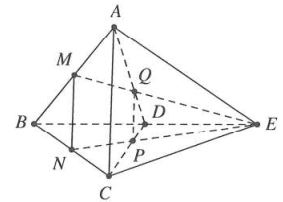
Thể tích khối tứ diện đều ABCD cạnh a là ${{V}_{ABCD}}=\frac{{{a}^{3}}\sqrt{2}}{12}$
Gọi $P=EN\cap CD$ và $Q=EM\cap AD$.
$\Rightarrow $P, Q lần lượt là trọng tâm của $\Delta BCE$ và $\Delta ABE$
Gọi S là diện tích tam giác BCD $\Rightarrow {{S}_{\Delta CDE}}={{S}_{\Delta BNE}}=S.$
Ta có: ${{S}_{\Delta PDE}}=\frac{1}{3}.{{S}_{\Delta CDE}}=\frac{S}{3}.$
Gọi h là chiều cao của tứ diện ABCD, suy ra
$d\left[ M;\left( BCD \right) \right]=\frac{h}{2};d\left[ Q;\left( BCD \right) \right]=\frac{h}{3}.$
Khi đó ${{V}_{M.BNE}}=\frac{1}{3}{{S}_{\Delta BNE}}.d\left( M;\left( BCD \right) \right)=\frac{S.h}{6}$;
Và ${{V}_{Q.PDE}}=\frac{1}{3}{{S}_{\Delta PDE}}.d\left( Q;\left( BCD \right) \right)=\frac{S.h}{27}$
Suy ra ${{V}_{PQD.NMB}}={{V}_{M.BNE}}-{{V}_{Q.PDE}}=\frac{S.h}{6}-\frac{S.h}{27}=\frac{7S.h}{54}=\frac{7}{18}.\frac{S.h}{3}=\frac{7}{18}.{{V}_{ABCD}}.$
Vậy thể tích khối đa diện chứa đỉnh A là $V={{V}_{ABCD}}-{{V}_{PQD.NMB}}=\frac{11}{18}.\frac{{{a}^{3}}\sqrt{2}}{12}=\frac{11\sqrt{2}{{a}^{3}}}{216}$. Chọn B.
| Bài tập 9: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, $AD=2,BA=BC=1.$ Cạnh bên SA vuông góc với đáy và $SA=\sqrt{2}$. Gọi H là hình chiếu vuông góc của A trên SB. Tính thể tích V của khối đa diện SAHCD.
A. $V=\frac{2\sqrt{2}}{3}.$ B. $V=\frac{4\sqrt{2}}{9}.$ C. $V=\frac{4\sqrt{2}}{3}.$ D. $V=\frac{2\sqrt{2}}{9}.$ |
Lời giải chi tiết

Tam giác vuông SAB, có $SB=\sqrt{S{{A}^{2}}+A{{B}^{2}}}=\sqrt{3}$
Gọi M là trung điểm của AD $\Rightarrow $ ABCM là hình vuông nên $CM=AB=a=\frac{AD}{2}.$
$\xrightarrow{{}}$Tam giác ACD vuông tại C.
Ta có ${{V}_{S.AHCD}}={{V}_{S.ACD}}+{{V}_{S.AHC}}$
- ${{V}_{S.ACD}}=\frac{1}{3}{{S}_{\Delta ACD.}}SA=\frac{1}{3}\left( \frac{1}{2}AD.AB \right)SA=\frac{\sqrt{2}}{3}$
- $\frac{{{V}_{S.AHC}}}{{{V}_{S.ABC}}}=\frac{SH}{SB}=\frac{S{{A}^{2}}}{S{{B}^{2}}}=\frac{2}{3}\Rightarrow {{V}_{S.AHC}}=\frac{2}{3}{{V}_{S.ABC}}=\frac{\sqrt{2}}{9}$
Vậy ${{V}_{S.AHCD}}=\frac{\sqrt{2}}{3}+\frac{\sqrt{2}}{9}=\frac{4\sqrt{2}}{9}.$ Chọn B
| Bài tập 10: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, $SA=a$ vuông góc với mặt phẳng đáy $\left( ABCD \right)$. Điểm M thuộc cạnh SA sao cho $\frac{SM}{SA}=k$. Xác định k sao cho mặt phẳng $\left( MBC \right)$ chia khối chóp đã cho thành hai phần có thể tích bằng nhau.
A. $k=\frac{-1+\sqrt{3}}{2}.$ B. $k=\frac{-1+\sqrt{5}}{2}.$ C. $k=\frac{-1+\sqrt{2}}{2}.$ D. $k=\frac{1+\sqrt{5}}{4}.$ |
Lời giải chi tiết
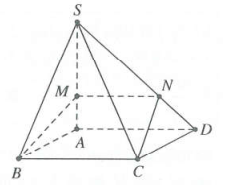
Cách 1. Kẻ $MN//AD\left( N\in SD \right)\xrightarrow{{}}\frac{SN}{SD}=\frac{SM}{SA}=k.$
Khi đó mặt phẳng $\left( MBC \right)$ chia khối chóp thành hai phần là S.MBCN và AMBDNC.
Ta có ${{V}_{S.MBCN}}={{V}_{S.MBC}}+{{V}_{S.MCN}}.$
$\frac{{{V}_{S.MBC}}}{{{V}_{S.ABC}}}=\frac{SM}{SA}=k\Rightarrow {{V}_{S.MBC}}=k.{{V}_{S.ABC}}.$
$\frac{{{V}_{S.MCN}}}{{{V}_{S.ACD}}}=\frac{SM}{SA}.\frac{SN}{SD}={{k}^{2}}\Rightarrow {{V}_{S.MCN}}={{k}^{2}}.{{V}_{S.ACD}}.$
Lại có ${{V}_{S.MBCN}}=\frac{1}{2}.{{V}_{S.ABCD}}\Rightarrow k.{{V}_{S.ABC}}+{{k}^{2}}.{{V}_{S.ACD}}=\frac{1}{2}.{{V}_{S.ABCD}}$
$\Rightarrow k.\frac{{{V}_{S.ABCD}}}{2}+{{k}^{2}}.\frac{{{V}_{S.ABCD}}}{2}=\frac{1}{2}.{{V}_{S.ABCD}}\xrightarrow{{}}k+{{k}^{2}}=1\Rightarrow k=\frac{-1+\sqrt{5}}{2}.$
Cách 2: Với $\frac{SA}{SM}=\frac{1}{k};\frac{SB}{SB}=1;\frac{SC}{SC}=1;\frac{SD}{SN}=\frac{1}{k}$
Áp dụng công thức, ta được $\frac{{{V}_{S.MBCN}}}{{{V}_{S.ABCD}}}=\frac{2.\frac{1}{k}+2}{4.\frac{1}{k}.\frac{1}{k}}=\frac{{{k}^{2}}+1}{2}=\frac{1}{2}\Rightarrow k=\frac{-1+\sqrt{5}}{2}.$ Chọn B.
| Bài tập 11: Cho hình chóp đều S.ABCD. Gọi N là trung điểm SB, M là điểm đối xứng với B qua A. Mặt phẳng $\left( MNC \right)$chia khối chóp S.ABCD thành hai phần có thể tích lần lượt là ${{V}_{1}},{{V}_{2}}$ với ${{V}_{1}}<{{V}_{2}}$. Tính tỉ số thể tích $\frac{{{V}_{1}}}{{{V}_{2}}}$.
A. $\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{5}{7}$ B. $\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{5}{11}$ C. $\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{5}{9}$ D. $\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{5}{13}$ |
Lời giải chi tiết
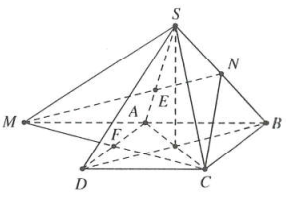
Gọi h, S lần lượt là chiều cao và diện tích đáy của khối chóp S.ABCD. Khi đó ${{V}_{S.ABCD}}=\frac{1}{3}S.h.$
Nối MN cắt SA tại E, MC cắt AD tại F.
Tam giác SBM có A, N lần lượt là trung điểm của BM và SB. Suy ra E là trọng tâm tam giác SBM.
Vì ACDM là hình bình hành nên F là trung điểm MC.
Ta có ${{V}_{BNC.AEF}}={{V}_{ABCEN}}+{{V}_{E.ACF}}$
$\frac{{{V}_{S.ENC}}}{{{V}_{S.ABC}}}=\frac{SE}{SA}.\frac{SN}{SB}=\frac{2}{3}\times \frac{1}{2}=\frac{1}{3}\xrightarrow{{}}{{V}_{S.ENC}}=\frac{1}{3}{{V}_{S.ABC}}$
$\xrightarrow[{}]{}{{V}_{ABCEN}}=\frac{2}{3}{{V}_{S.ABC}}=\frac{2}{3}\left( \frac{1}{2}{{V}_{S.ABCD}} \right)=\frac{1}{3}{{V}_{S.ABCD}}.$
${{V}_{E.ACF}}=\frac{1}{3}{{S}_{\Delta ACF}}.d\left( E;\left( ACF \right) \right)=\frac{1}{3}.\frac{1}{4}S.\frac{1}{3}h=\frac{1}{12}.{{V}_{S.ABCD}}.$
Do đó ${{V}_{BNC.AEF}}={{V}_{ABCEN}}+{{V}_{E.ACF}}=\frac{1}{3}{{V}_{S.ABCD}}+\frac{1}{12}.{{V}_{S.ABCD}}=\frac{5}{12}.{{V}_{S.ABCD}}={{V}_{1}}.$
Suy ra ${{V}_{2}}=\frac{7}{12}.{{V}_{S.ABCD}}\xrightarrow{{}}\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{5}{7}.$ Chọn A.
| Ví dụ 12: Cho khối hộp $ABCD.{A}'{B}'{C}'{D}’$. Gọi M thuộc cạnh AB sao cho $MB=2MA.$ Mặt phẳng $\left( M{B}'{D}’ \right)$ chia khối hộp thành hai phần. Tính tỉ số thể tích của hai phần đó.
A. $\frac{5}{12}.$ B. $\frac{7}{17}.$ C. $\frac{13}{41}.$ D. $\frac{5}{17}.$ |
Lời giải
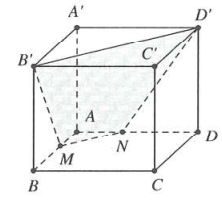
Lý thuyết bổ sung:
Cho hình chóp cụt $ABC.{A}'{B}'{C}’$ có chiều cao h, ${{S}_{1}}$ là diện tích tam giác ABC, ${{S}_{2}}$ là diện tích tam giác ${A}'{B}'{C}’.$ Thể tích khối chóp cụt $ABC.{A}'{B}'{C}’$ là $$
Qua M kẻ đường thẳng $d//BD,$ cắt AD tại N
Suy ra thiết diện cắt bởi mặt phẳng $\left( M{B}'{D}’ \right)$ là $MN{D}'{B}’$
Khi đó ${{V}_{ABCD.{A}'{B}'{C}'{D}’}}={{V}_{AMN.{A}'{B}'{D}’}}+{{V}_{{B}'{C}'{D}’.MBCDN}}$
Đặt $A{A}’=h;{{S}_{ABCD}}=S\xrightarrow{{}}{{V}_{ABCD.{A}'{B}'{C}'{D}’}}=S.h$
Áp dụng công thức tính thể tích chóp cụt, ta có
${{V}_{AMN.{A}'{B}'{D}’}}=\frac{1}{3}A{A}’.\left( {{S}_{\Delta AMN}}+{{S}_{\Delta {A}'{B}'{D}’}}+\sqrt{{{S}_{\Delta AMN}}.{{S}_{\Delta {A}'{B}'{D}’}}} \right)$
Mà $\frac{{{S}_{\Delta AMN}}}{{{S}_{\Delta ABD}}}=\frac{AM}{AB}.\frac{AN}{AD}=\frac{1}{9}\Rightarrow {{S}_{\Delta AMN}}=\frac{1}{9}{{S}_{\Delta ABD}}=\frac{S}{18}.$
Và ${{S}_{\Delta {A}'{B}'{D}’}}=\frac{S}{2}\xrightarrow{{}}{{V}_{AMN.{A}'{B}'{D}’}}=\frac{1}{3}h\left( \frac{S}{18}+\frac{S}{2}+\sqrt{\frac{S}{18}.\frac{S}{2}} \right)=\frac{13}{54}V$
Vậy tỉ số thể tích cần tính là $\frac{13}{54}:\left( 1-\frac{13}{54} \right)=\frac{13}{41}.$ Chọn C.
| Ví dụ 13: Cho hình lập phương $ABCD.{A}'{B}'{C}'{D}’$. Gọi I là trung điểm của $B{B}’,$ mặt phẳng $\left( DI{C}’ \right)$ chia khối lập phương thành 2 phần có tỉ số thể tích phần bé chia phần lớn bằng
A. $\frac{3}{8}$ B. $\frac{2}{3}$ C. $\frac{7}{17}.$ D. $\frac{5}{12}$ |
Lời giải
Tham khảo hình vẽ dưới đây:
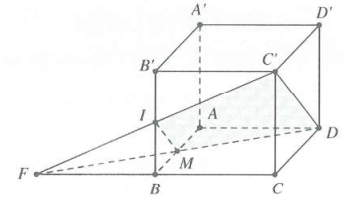
Đặt $A{A}’=h;{{S}_{ABCD}}=S\xrightarrow{{}}{{V}_{ABCD.{A}'{B}'{C}'{D}’}}=S.h$
Nối $I{C}’$ cắt BC tại F; nối FD cắt AB tại M.
Suy ra $mp\left( DI{C}’ \right)$ chia khối lập phương thành hai khối $IBM.{C}’CD$ và $IMA{A}'{B}’.{C}’D{D}’$
Vì M là trung điểm của AB mà $BM//CD\Rightarrow \frac{FB}{FC}=\frac{1}{2}.$
Ta có $BI//C{C}’\Rightarrow \frac{IB}{C{C}’}=\frac{FB}{FC}=\frac{1}{2}\Rightarrow {{S}_{\Delta IBM}}=\frac{1}{4}{{S}_{\Delta BA{B}’}}=\frac{1}{8}{{S}_{AB{B}'{A}’}}$
Áp dụng công thức tính thể tích chóp cụt, ta được
${{V}_{IBM.{C}’CD}}=\frac{1}{3}BC.\left( {{S}_{\Delta IBM}}+{{S}_{\Delta {C}’CD}}+\sqrt{{{S}_{\Delta IBM}}.{{S}_{\Delta {C}’CD}}} \right)=\frac{1}{3}h.\left( \frac{S}{8}+\frac{S}{2}+\sqrt{\frac{S}{8}.\frac{S}{2}} \right)=\frac{7}{24}.Sh$
Do đó, thể tích khối $IMA{A}'{B}’.{C}’D{D}’$ là ${{V}_{IMA{A}'{B}’.{C}’D{D}’}}=V-\frac{7}{24}V=\frac{17}{24}V.$
Vậy tỉ số cần tính là $\frac{7}{24}:\frac{17}{24}=\frac{7}{17}.$ Chọn C.
| Ví dụ 14: Cho khối lăng trụ $ABC.{A}'{B}'{C}’$ có thể tích bằng 1. Gọi M, N lần lượt là trung điểm của các đoạn thẳng $A{A}’$ và $B{B}’$. Đường thẳng CM cắt đường thẳng ${C}'{A}’$ tại P, đường thẳng CN cắt đường thẳng ${C}'{B}’$ tại Q. Thể tích của khối đa diện lồi ${A}’MP{B}’NQ$ bằng:
A. 1 B. $\frac{1}{3}$ C. $\frac{1}{2}$ D. $\frac{2}{3}$ |
Lời giải
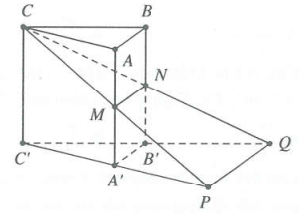
Ta có: ${{V}_{C.ABNM}}=\frac{1}{2}{{V}_{C.AB{B}'{A}’}}=\frac{1}{2}.\frac{2}{3}{{V}_{ABC.{A}'{B}'{C}’}}=\frac{1}{3}.$
Suy ra ${{V}_{CMN.{A}'{B}'{C}’}}={{V}_{ABC.{A}'{B}'{C}’}}-{{V}_{C.ABNM}}=1-\frac{1}{3}=\frac{2}{3}.$
Lại có ${{V}_{C.{C}’PQ}}={{V}_{CMN.{A}'{B}'{C}’}}+{{V}_{{A}’MP{B}’NQ}}$
$\Rightarrow {{V}_{{A}’MP{B}’NQ}}={{V}_{C.{C}’PQ}}-\frac{2}{3}.$ Mà ${{S}_{\Delta {C}’PQ}}=4{{S}_{{A}'{B}'{C}’}}$
$\Rightarrow {{V}_{C.{C}’PQ}}=4{{V}_{{C}’.{A}'{B}'{C}’}}=4.\frac{1}{3}{{V}_{ABC.{A}'{B}'{C}’}}=\frac{4}{3}.$
Vậy ${{V}_{{A}’MP{B}’NQ}}=\frac{4}{3}-\frac{2}{3}=\frac{2}{3}.$ Chọn D.
