Cách viết phương trình mặt phẳng trong không gian từ A-Z đủ dạng
1. Vectơ pháp tuyến của mặt phẳng
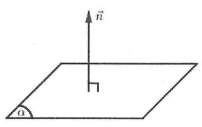
Vectơ $\overrightarrow{n}\ne \overrightarrow{0}$ được gọi là vectơ pháp tuyến của mặt phẳng (α) nếu giá của $\overrightarrow{n}$ vuông góc với (α).
Nêu 2 vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ không cùng phương và giá của chúng song song với một mặt phẳng (α) (hoặc nằm trên (α)) thì vectơ $\overrightarrow{n}=\left[ \overrightarrow{u},\overrightarrow{v} \right]$ là một vectơ pháp tuyến của mặt phẳng (α).
Chú ý: Nếu $\overrightarrow{n}\ne \overrightarrow{0}$là vectơ pháp tuyến của mặt phẳng (α) thì $k.\overrightarrow{n}\,\,(k\in \mathbb{R},k\ne 0)$ cũng là một vectơ pháp tuyến của mặt phẳng (α).
Bài tập: Nếu $\overrightarrow{n}=(2;4;6)$là một vectơ pháp tuyến của mặt phẳng (α) thì ${{\overrightarrow{n}}_{1}}=(1;2;3)$ cũng là một vectơ pháp tuyến của mặt phẳng (α). Trong quá trình tính toán ta nên chọn vectơ đơn giản nhất.
2. Phương trình tổng quát của mặt phẳng
Mặt phẳng đi qua điểm $M\left( {{x}_{0}};{{y}_{0}};{{z}_{0}} \right)$ có vectơ pháp tuyến là $\overrightarrow{n}=\left( A;B;C \right)$ có phương trình tổng quát là $A\,(x-{{x}_{0}})+B\,(y-{{y}_{0}})+C\,(z-{{z}_{0}})=0.$
Mỗi mặt phẳng đều có phương trình tổng quát dạng Ax+ By + Cz + D = 0 với A2 + B2 + C2 > 0.
Ngược lại mỗi phương trình có dạng trên đều là phương trình của một mặt phẳng.
Nếu mặt phẳng (α) có phương trình Ax + By + Cz + D = 0 thì vectơ $\overrightarrow{n}=(A;B;C\text{)}$ là vectơ pháp tuyến của mặt phẳng (α).
3. Phương trình mặt phẳng theo đoạn chắn
Mặt phẳng (α) không đi qua gốc O, cắt trục Ox tại điểm $A\left( a;0;0 \right)$, cắt trục Oy tại điểm $B\left( 0;b;0 \right)$ và cắt trục Oz tại điểm $C\left( 0;0;c \right)$ có phương trình $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$ (abc≠0).
Phương trình này được gọi là phương trình theo đoạn chắn của mặt phẳng (α).
4. Một số cách xác định vectơ pháp tuyến của mặt phẳng hay gặp:
• (P) đi qua ba điểm phân biệt A, B, C thì có vectơ pháp tuyến ${{\overrightarrow{n}}_{p}}=\left[ \overrightarrow{AB},\overrightarrow{AC} \right]$
• (P) đi qua điểm A và song song với (Q) thì ta chọn cho ${{\overrightarrow{n}}_{p}}={{\overrightarrow{n}}_{Q}}$
• (P) đi qua điểm A và vuông góc với hai mặt phẳng phân biệt (α), (β) thì $\left\{ \begin{array} {} {{\overrightarrow{n}}_{p}}\bot {{\overrightarrow{n}}_{\alpha }} \\ {} {{\overrightarrow{n}}_{p}}\bot {{\overrightarrow{n}}_{\beta }} \\ \end{array} \right.\xrightarrow{{}}{{\overrightarrow{n}}_{p}}=\left[ {{\overrightarrow{n}}_{\alpha }},\overrightarrow{{{n}_{\beta }}} \right]$
• (P) đi qua điểm A và song song với hai vectơ thì $\overrightarrow{a},\,\,\overrightarrow{b}$ thì $\left\{ \begin{array} {} {{\overrightarrow{n}}_{p}}\bot \overrightarrow{a} \\ {} {{\overrightarrow{n}}_{p}}\bot \overrightarrow{b} \\ \end{array} \right.\xrightarrow{{}}{{\overrightarrow{n}}_{p}}=\left[ \overrightarrow{a},\overrightarrow{b} \right]$
• (P) đi qua điểm A, B và vuông góc với (α) thì $\left\{ \begin{array} {} {{\overrightarrow{n}}_{p}}\bot \overrightarrow{AB} \\ {} {{\overrightarrow{n}}_{p}}\bot \overrightarrow{{{n}_{\alpha }}} \\ \end{array} \right.\to {{\overrightarrow{n}}_{p}}=\left[ \overrightarrow{AB},\overrightarrow{{{n}_{\alpha }}} \right]$
