Cách viết phương trình đường thẳng trong không gian oxyz từ A-Z đủ dạng
1. Vectơ chỉ phương của đường thẳng
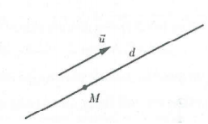
Vectơ $\overrightarrow{u}\ne \overrightarrow{0}$ được gọi là vectơ chỉ phương của đường thẳng d nếu giá của $\overrightarrow{u}$ song song hoặc trùng với d.
Chú ý: Nếu $\overrightarrow{u}\ne \overrightarrow{0}$ là vectơ chỉ phương của đường thẳng d thì $k.\overrightarrow{u}\,\,(k\in \mathbb{R};k\ne 0)$ cũng là một vectơ chỉ phương của đường thẳng d.
2. Phương trình tham số và phương trình chính tắt của đường thẳng
Đường thẳng đi qua điểm $M\left( {{x}_{0}};{{y}_{0}};{{z}_{0}} \right)$ với vectơ chỉ phương $\overrightarrow{u}=(a;b;c)$ có:
+ Phương trình tham số : $\left\{ \begin{array} {} x={{x}_{0}}+at \\ {} y={{y}_{0}}+bt \\ {} z={{z}_{0}}+ct \\ \end{array} \right.\,\,\,(t\in \mathbb{R}).$
(Với mỗi giá trị t cho ta các giá trị tương ứng $x,\,\,y,\,\,z$ tương ứng là tọa độ của một điểm M thuộc đường thẳng).
+) Phương trình chính tắc là: $\frac{x-{{x}_{0}}}{a}=\frac{y-{{y}_{0}}}{b}=\frac{z-{{z}_{0}}}{c}$ với điều kiện abc ≠ 0.
3. Xác định vecto chỉ phương
Cho 2 mặt phẳng (P) và (Q) lần lượt có phương trình là $\text{Ax}+By+Cz+D=0$ và
$\text{A }\!\!’\!\!\text{ x}+B’y+C’z+D’=0$ với điều kiện $A:B:C\ne A’:B’:C’$
Điều kiện trên chứng tỏ hai mặt phẳng đó cắt nhau. Gọi d là đường thẳng giao tuyến của chúng.
Đường thẳng d gồm những điểm M (x;y;z) vừa thuộc mặt phẳng (P) vừa thuộc mặt phẳng (Q) nên tọa độ điểm M là nghiệm của hệ phương trình $\left\{ \begin{array} {} Ax+By+Cz+D=0 \\ {} A’x+B’y+C’z+D’=0 \\ \end{array} \right..$
Khi đó $\overrightarrow{u}=\left[ \overrightarrow{{{n}_{(P)}}},\overrightarrow{{{n}_{Q}}} \right]$ với $\overrightarrow{{{n}_{(P)}}}=(A;B;C);\,\,\overrightarrow{{{n}_{Q}}}=(A’;B’;C’)$ là một vectơ chỉ phương của đường
thẳng d.
4. Một số cách xác định vectơ chỉ phương của đường thẳng hay gặp:
• (d) đi qua điểm A và song song với đường thẳng (∆) thì ta chọn cho ${{\overrightarrow{u}}_{d}}={{\overrightarrow{u}}_{\Delta }}$
• (d) đi qua điểm A và vuông góc với hai đường thẳng (d1), (d2) thì$\left\{ \begin{array} {} {{\overrightarrow{u}}_{d}}\bot {{\overrightarrow{u}}_{{{d}_{1}}}} \\ {} {{\overrightarrow{u}}_{d}}\bot {{\overrightarrow{u}}_{{{d}_{2}}}} \\ \end{array} \right.\to {{\overrightarrow{u}}_{d}}=\left[ {{\overrightarrow{u}}_{{{d}_{1}}}},{{\overrightarrow{u}}_{{{d}_{2}}}} \right]$
• (d) đi qua điểm A và song song với hai mặt phẳng (α), (β) thì $\left\{ \begin{array} {} {{\overrightarrow{u}}_{d}}\bot \overrightarrow{{{n}_{\alpha }}} \\ {} {{\overrightarrow{u}}_{d}}\bot \overrightarrow{{{n}_{\beta }}} \\ \end{array} \right.\xrightarrow{{}}{{\overrightarrow{u}}_{d}}=\left[ \overrightarrow{{{n}_{\alpha }}},\overrightarrow{{{n}_{\beta }}} \right]$
• (d) đi qua điểm A và vuông góc với đường thẳng (∆); song song với mặt phẳng (P) thì
$\left\{ \begin{array} {} {{\overrightarrow{u}}_{d}}\bot {{\overrightarrow{u}}_{\Delta }} \\ {} {{\overrightarrow{u}}_{d}}\bot {{\overrightarrow{n}}_{P}} \\ \end{array} \right.\to {{\overrightarrow{u}}_{d}}=\left[ {{\overrightarrow{u}}_{\Delta }},{{\overrightarrow{n}}_{P}} \right]$
