Tính nhanh Góc giữa đường cao và mặt bên – bài tập có đáp án
Phương pháp giải nhanh góc giữa đường cao và mặt bên
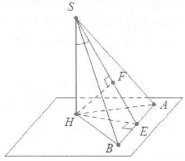
Tìm góc giữa đường cao SH và mặt phẳng (SAB).
Dựng $HE\bot AB,HF\bot SE.$
Ta có: $AB\bot SH\Rightarrow AB\bot \left( SHE \right)\Rightarrow AB\bot HF.$
Mặt khác $HF\bot SE\Rightarrow HF\bot \left( SAB \right)\Rightarrow F$ là hình chiếu vuông góc của H trên mặt phẳng (SAB).
Vậy $\widehat{\left( SH;SAB \right)}=\widehat{\left( HF;SF \right)}=\widehat{HSF}.$
Bài tập xác định, tính góc giữa đường cao và mặt bên
| Bài tập 1: Cho hình chóp S.ABC, có đáy ABC là tam giác đều cạnh 2a. Cạnh bên $SA=a\sqrt{3}$ và vuông góc với đáy. Tính góc giữa SA và mặt phẳng (SBC). |
Lời giải chi tiết
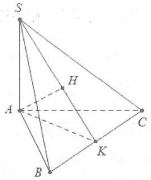
Từ A kẻ AK vuông góc với BC tại K.
Ta có : $SA\bot BC$ và $AK\bot BC\Rightarrow BC\bot \left( SAK \right).$
Kẻ $AH\bot SK,H\in SK$. Mà $BC\bot AH.$
Suy ra $AH\bot \left( SBC \right)\Rightarrow \widehat{\left( SA;\left( SBC \right) \right)}=\widehat{ASH}=\widehat{ASK}.$
Tam giác SAK vuông tại A, có $SA=AK=a\sqrt{3}.$
$\Rightarrow $ tam giác SAK vuông cân tại A nên $ASK=45{}^\circ .$
Vậy $\widehat{\left( SA;\left( SBC \right) \right)}=45{}^\circ .$
| Bài tập 2: Cho hình chóp S.ABCD có đáy là hình chữ nhật có $AB=a,AD=2a,SA=2a$ và $SA\bot \left( ABCD \right)$. Tính tan góc giữa SA và các mặt phẳng (SBC), (SBD) và (SCD). |
Lời giải chi tiết
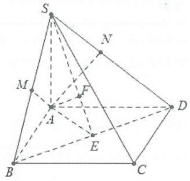
Do $\left\{ \begin{array} {} BC\bot AB \\ {} BC\bot SA \\ \end{array} \right.\Rightarrow BC\bot \left( SAB \right).$
Dựng $AM\bot SB\Rightarrow AM\bot \left( SBC \right)\Rightarrow $ M là hình chiếu vuông góc của A trên (SBC).
Khi đó: $\widehat{\left( SA;\left( SBC \right) \right)}=\widehat{ASM}=\widehat{ASB}=\alpha .$
Do đó $\tan \alpha =\frac{AB}{SA}=\frac{1}{2}.$
Tương tự ta có: $\widehat{\left( SA;\left( SCD \right) \right)}=\widehat{ASD}=\beta $ và $\tan \beta =\frac{AD}{SA}=1.$
Dựng $AE\bot BD,AF\bot SE$ ta có: $\left\{ \begin{array} {} BD\bot AE \\ {} BD\bot SA \\ \end{array} \right.\Rightarrow BD\bot \left( SAE \right)\Rightarrow BD\bot AF.$
Mặt khác $AF\bot SE\Rightarrow AF\bot \left( SBD \right)\Rightarrow \widehat{\left( SA;\left( SBD \right) \right)}=\widehat{ASF}=\widehat{ASE}.$
Khi đó $\tan \widehat{ASE}=\frac{AE}{SA}$, trong đó $AE=\frac{AB.AD}{\sqrt{A{{B}^{2}}+A{{D}^{2}}}}=\frac{2a}{\sqrt{5}}\Rightarrow \tan \widehat{ASE}=\frac{AE}{SA}=\frac{1}{\sqrt{5}}.$
| Bài tập 3: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B có $AD=2AB=2CD=2a$ và $SA\bot \left( ABCD \right)$. Biết rằng SC tạo với đáy một góc $60{}^\circ $. Tính tan góc giữa SA và các mặt phẳng (SBC), (SCD) và (SBD). |
Lời giải chi tiết
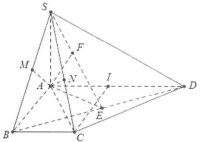
Ta có: $AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=a\sqrt{2}$
Do $SA\bot \left( ABCD \right)\Rightarrow \widehat{\left( SC;\left( ABCD \right) \right)}=\widehat{SCA}=60{}^\circ .$
Suy ra $SA=AC\tan 60{}^\circ =a\sqrt{6}.$
Dựng $AM\bot SB$ có $\left\{ \begin{array} {} BC\bot SA \\ {} BC\bot AB \\ \end{array} \right.\Rightarrow BC\bot AM.$
Do đó $AM\bot \left( SBC \right)\Rightarrow $ M là hình chiếu của A trên mặt phẳng (SBC).
Suy ra $\widehat{\left( SA;\left( SBC \right) \right)}=\widehat{ASM}=\widehat{ASB}.$
Ta có: $\tan \widehat{ASB}=\frac{AB}{SA}=\frac{a}{a\sqrt{6}}=\frac{1}{\sqrt{6}}.$
Gọi I là trung điểm của AD $\Rightarrow $ ABCI là hình vuông cạnh a $\Rightarrow CI=\frac{AD}{2}=a\Rightarrow \Delta ACD$ vuông tại C. Khi đó $\left\{ \begin{array} {} CD\bot SA \\ {} CD\bot AC \\ \end{array} \right.\Rightarrow CD\bot \left( SAC \right).$
Dựng $AN\bot SC\Rightarrow \widehat{\left( SA;\left( SCD \right) \right)}=\widehat{ASN}=\widehat{ASC}.$ Ta có: $\tan \widehat{ASC}=\frac{AC}{SA}=\frac{a\sqrt{2}}{a\sqrt{6}}=\frac{1}{\sqrt{3}}.$
Dựng $\left\{ \begin{array} {} AE\bot BD \\ {} AF\bot SE \\ \end{array} \right.\Rightarrow \widehat{\left( SA;\left( SBD \right) \right)}=\widehat{ASF}=\widehat{ASE}.$
Mặt khác $AE=\frac{AB.AD}{\sqrt{A{{B}^{2}}+A{{D}^{2}}}}=\frac{2a}{\sqrt{5}}\Rightarrow \tan \widehat{ASE}=\frac{AE}{SA}=\frac{\sqrt{30}}{15}.$
| Bài tập 4: Cho hình chóp S.ABCD, có đáy là nửa lục giác đều cạnh a, $AD=2a$. Biết $SA\bot \left( ABCD \right)$ và đường thẳng SB tạo với đáy một góc 60°.
a) Tính tan góc tạo bởi SA và (SBC). b) Tính góc tạo bởi SA và (SCD). |
Lời giải chi tiết
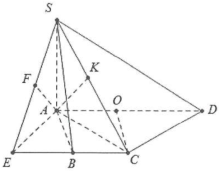
a) Gọi O là trung điểm của AD $\Rightarrow $ OABC là hình thoi cạnh a $\Rightarrow CO=a=\frac{1}{2}AD\Rightarrow \Delta ACD$ vuông tại C.
Do $SA\bot \left( ABCD \right)\Rightarrow \widehat{\left( SB;\left( ABCD \right) \right)}=\widehat{SBA}=60{}^\circ .$
$\Rightarrow SA=AB\tan 60{}^\circ =a\sqrt{3}$, $AC=\sqrt{A{{D}^{2}}-C{{D}^{2}}}=a\sqrt{3}.$
Dựng $AE\bot BC$, $AF\bot SE\Rightarrow \widehat{\left( SA;\left( SBC \right) \right)}=\widehat{ASF}=\widehat{ASE}.$
Do $\widehat{ABE}=120{}^\circ \Rightarrow \widehat{ABE}=60{}^\circ .$
Mặt khác $AE=AB\sin \widehat{ABE}=AB\sin 60{}^\circ =\frac{a\sqrt{3}}{2}.$
Suy ra $\tan \widehat{\left( SA;\left( SBC \right) \right)}=\tan \widehat{ASE}=\frac{AE}{SA}=\frac{1}{2}.$
b) Do $\left\{ \begin{array} {} CD\bot SA \\ {} CD\bot AC \\ \end{array} \right.\Rightarrow CD\bot \left( SAC \right).$ Dựng $AK\bot SC\Rightarrow AK\bot \left( SCD \right)$
Khi đó $\widehat{\left( SA;\left( SCD \right) \right)}=\widehat{ASK}=\widehat{ASC}=\varphi .$
Ta có: $\tan \varphi =\frac{AC}{SA}=\frac{a\sqrt{3}}{a\sqrt{3}}=1\Rightarrow \varphi =45{}^\circ .$ Vậy $\widehat{\left( SA;\left( SCD \right) \right)}=45{}^\circ .$
| Bài tập 5: Cho hình lăng trụ $ABC.{A}'{B}'{C}’$ có đáy là tam giác đều cạnh a, hình chiếu vuông góc của ${B}’$ lên mặt phẳng đáy trùng với trung điểm H của cạnh AB, đường cao ${B}’H=\frac{3a}{4}$. Tính cosin góc giữa đường thẳng ${B}’H$ và mặt phẳng $\left( BC{C}'{B}’ \right)$. |
Lời giải chi tiết
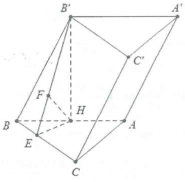
Dựng $HE\bot BC,HF\bot {B}’E$ ta có: $\left\{ \begin{array} {} BC\bot {B}’H \\ {} BC\bot HE \\ \end{array} \right.$ suy ra $BC\bot HF\Rightarrow HF\bot \left( {B}’BC{C}’ \right)\Rightarrow \widehat{\left( {B}’H;\left( BC{C}'{B}’ \right) \right)}$
$=\widehat{H{B}’F}=\widehat{H{B}’E}.$
Ta có: $HE=HB\sin \widehat{HBE}=\frac{a}{2}\sin 60{}^\circ =\frac{a\sqrt{3}}{4}$
Do đó $\cos \widehat{H{B}’E}=\frac{{B}’H}{{B}’E}=\frac{{B}’H}{\sqrt{{B}'{{H}^{2}}+H{{E}^{2}}}}=\frac{\sqrt{3}}{2}.$