Cách tính Khoảng cách từ một điểm bất kỳ đến mặt bên.
Phương pháp tính khoảng cách trong không gian
– Nếu $AB//\left( \alpha \right)$ thì ta có $d\left( A;\left( \alpha \right) \right)=d\left( B;\left( \alpha \right) \right)$.
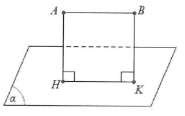
– Nếu AB cắt $\left( \alpha \right)$ tại I thì ta có: $\frac{d\left( A;\left( \alpha \right) \right)}{d\left( B;\left( \alpha \right) \right)}=\frac{AI}{BI}$ (định lý Talet).
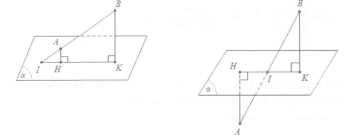
Xét bài toán: Tính khoảng cách từ điểm C bất kỳ đến mặt phẳng bên $\left( SAB \right)$.
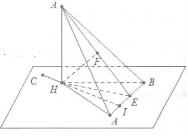
Nếu $CH//\left( SAB \right)\Rightarrow d\left( C;\left( SAB \right) \right)=d\left( H;\left( SAB \right) \right).$
Nếu $CH\cap \left( SAB \right)=I\Rightarrow \frac{d\left( C;\left( SAB \right) \right)}{d\left( H;\left( SAB \right) \right)}=\frac{CI}{HI}.$
Quay trở về bài toán tính khoảng cách từ chân đường cao H đến mặt phẳng bên.
Bài tập khoảng cách trong không gian có đáp án chi tiết
| Bài tập 1: Cho hình chóp S.ABC có đáy là tam giác vuông tại B có $AB=a,BC=2a$. Tam giác SAC cân tại S và thuộc mặt phẳng vuông góc với đáy. Biết $SB=\frac{3a}{2}$, tính:
a) Khoảng cách từ điểm C đến mặt phẳng $\left( SAB \right)$. b) Khoảng cách từ A đến mặt phẳng $\left( SBC \right)$. |
Lời giải chi tiết
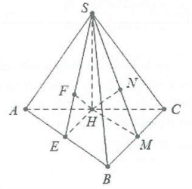
a) Gọi H là trung điểm của AC$\Rightarrow SH\bot AC$
Mặt khác $\left( SAC \right)\bot \left( ABC \right)\Rightarrow SH\bot \left( ABC \right)$
Ta có: $BH=\frac{AC}{2}=\frac{\sqrt{A{{B}^{2}}+B{{C}^{2}}}}{2}=\frac{a\sqrt{5}}{2}$ (trong tam giác vuông thì trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy).
Do đó $SH=\sqrt{S{{B}^{2}}-B{{H}^{2}}}=a$
Dựng $HE\bot AB,HF\bot SE$ khi đó $HF\bot \left( SAB \right)$
Do vậy $d\left( H;\left( SCD \right) \right)=HF$. Lại có $HE=\frac{BC}{2}=a$
Mặt khác $\frac{1}{H{{F}^{2}}}=\frac{1}{H{{E}^{2}}}+\frac{1}{S{{H}^{2}}}\Rightarrow HF=\frac{SH.HE}{\sqrt{S{{H}^{2}}+H{{E}^{2}}}}=\frac{a\sqrt{2}}{2}$
Lại có $\frac{d\left( C;\left( SAB \right) \right)}{d\left( H;\left( SAB \right) \right)}=\frac{CA}{HA}=2\Rightarrow d\left( C;\left( SAB \right) \right)=2d\left( H;\left( SAB \right) \right)=a\sqrt{2}$.
b) Dựng $HM\bot BC,HN\bot SM\Rightarrow d\left( H;\left( SBC \right) \right)=HN$.
Trong đó $HM=\frac{AB}{2}=\frac{a}{2}\Rightarrow HN=\frac{SH.HM}{\sqrt{S{{H}^{2}}+H{{M}^{2}}}}=\frac{a}{\sqrt{5}}$
Lại có $\frac{d\left( A;\left( SBC \right) \right)}{d\left( H;\left( SBC \right) \right)}=\frac{AC}{HC}=2\Rightarrow d\left( A;\left( SBC \right) \right)=2d\left( H;\left( SBC \right) \right)=2HN=\frac{2a}{\sqrt{5}}$.
| Bài tập 2: Cho hình chóp S.ABC có $SA\bot \left( ABC \right)$, đáy là tam giác đều cạnh a. Biết $SB=a\sqrt{5}$.
a) Tính khoảng cách từ trung điểm K của SA đến mặt phẳng $\left( SBC \right)$. b) Tính khoảng cách từ trung điểm I của SB đến mặt phẳng $\left( SAC \right)$. |
Lời giải chi tiết
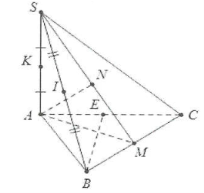
a) Dựng $AM\bot BC\Rightarrow AM=AC\operatorname{sinC}=a\sin 60{}^\circ =\frac{a\sqrt{3}}{2}$
Dựng $AN\bot SM$. Do $\left\{ \begin{array} {} BC\bot SA \\
{} BC\bot AM \\ \end{array} \right.\Rightarrow BC\bot AN$
Lại có $AN\bot SM\Rightarrow AN\bot \left( SBC \right)$
Mặt khác $SA=\sqrt{S{{B}^{2}}-A{{B}^{2}}}=2a,\frac{1}{A{{N}^{2}}}=\frac{1}{S{{A}^{2}}}+\frac{1}{A{{M}^{2}}}$
$\Rightarrow d\left( A;\left( SBC \right) \right)=AN=\frac{2a\sqrt{57}}{19}$
Do K là trung điểm của SA nên ta có $\frac{d\left( K;\left( SBC \right) \right)}{d\left( A;\left( SBC \right) \right)}=\frac{KS}{AS}=\frac{1}{2}\Rightarrow d\left( K;\left( SBC \right) \right)=\frac{1}{2}AN=\frac{a\sqrt{57}}{19}$.
b) Dựng $BE\bot AC\Rightarrow BE=\frac{a\sqrt{3}}{2}$
Mặt khác $BE\bot SA\Rightarrow BE\bot \left( SAC \right)\Rightarrow d\left( B;\left( SAC \right) \right)=BE=\frac{a\sqrt{3}}{2}$
Do $\frac{d\left( B;\left( SAC \right) \right)}{d\left( I;\left( SAC \right) \right)}=\frac{BS}{IS}=2\Rightarrow d\left( I;\left( SAC \right) \right)=\frac{1}{2}d\left( B;\left( SAC \right) \right)=\frac{a\sqrt{3}}{4}$.
| Bài tập 3: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 3a, hình chiếu vuông góc của đỉnh S trên mặt phẳng đáy và điểm H thuộc cạnh AB sao cho HB=2HA. Biết SC tạo với đáy một góc $45{}^\circ $. Tính các khoảng cách sau:
a) $d\left( B;\left( SAC \right) \right)$ b) $d\left( I;\left( SBC \right) \right)$ |
Lời giải chi tiết
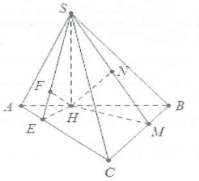
a) Tam giác ABC đều nên $\widehat{HAC}=60{}^\circ $.
Ta có: $HC=\sqrt{A{{H}^{2}}+A{{C}^{2}}-2AH.AC\cos 60{}^\circ }=a\sqrt{7}$
Mặt khác $\widehat{\left( SC;\left( ABC \right) \right)}=\widehat{SCH}=45{}^\circ \Rightarrow SH=HC=a\sqrt{7}$
Ta có:$\frac{BA}{HA}=\frac{d\left( B;\left( SAC \right) \right)}{d\left( H;\left( SAC \right) \right)}$
$\Rightarrow d\left( B;\left( SAC \right) \right)=3d\left( H;\left( SAC \right) \right)$
Dựng $HE\bot AC,HF\bot SE\Rightarrow HF\bot \left( SAC \right)$
Ta có: $HE=HA\sin 60{}^\circ =a\sin 60{}^\circ =\frac{a\sqrt{3}}{2}$
$\Rightarrow HF=\frac{HE.SH}{\sqrt{S{{H}^{2}}+H{{E}^{2}}}}=\frac{a\sqrt{651}}{31}\Rightarrow d\left( B;\left( SAC \right) \right)=3HF=\frac{3a\sqrt{651}}{31}$
b) Ta có: $\frac{d\left( A;\left( SBC \right) \right)}{d\left( H;\left( SBC \right) \right)}=\frac{AB}{HB}=\frac{3}{2}\Rightarrow d\left( A;\left( SBC \right) \right)=\frac{3}{2}d\left( H;\left( SBC \right) \right)$
Dựng $HM\bot BC,HN\bot SM\Rightarrow d\left( H;\left( SBC \right) \right)=HN$
Mặt khác $HM=HB\sin 60{}^\circ =2a\sin 60{}^\circ =a\sqrt{3}\Rightarrow HN=\frac{SH.HM}{\sqrt{S{{H}^{2}}+H{{M}^{2}}}}=\frac{a\sqrt{210}}{10}$
Do đó $d\left( A;\left( SBC \right) \right)=\frac{3}{2}HN=\frac{3a\sqrt{210}}{20}$.
| Bài tập 4: Cho hình chóp tam giác đều S.ABC có đáy là tam giác đều cạnh. Cạnh bên tạo với đáy góc $60{}^\circ $. Tính khoảng cách từ A đến mặt phẳng $\left( SBC \right)$. |
Lời giải chi tiết
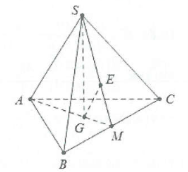
Gọi G là trọng tâm tam giác ABC$\Rightarrow SG\bot \left( ABC \right)$
Gọi M là trung điểm của BC$\Rightarrow $$BC\bot GM$, lại có: $BC\bot SG$suy ra $BC\bot \left( SGM \right)$.
Dựng $GE\bot SM\Rightarrow $$\left\{ \begin{array} {} GE\bot SM \\ {} GE\bot BC \\ \end{array} \right.\Rightarrow GE\bot (SBC)$
Do đó $d\left( G;\left( SBC \right) \right)=GE$
trong đó $GM=\frac{1}{3}AM=\frac{1}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{6},GA=\frac{2}{3}AM=\frac{a\sqrt{3}}{3}$
Do $SG\bot (ABC)\Rightarrow \widehat{\left( SA;\left( ABC \right) \right)}=\widehat{SAG}=60{}^\circ $$\Rightarrow SG=GA\tan 60{}^\circ =\frac{a\sqrt{3}}{3}\tan 60{}^\circ =a$
Do đó $GE=\frac{SG.GM}{\sqrt{S{{G}^{2}}+G{{M}^{2}}}}=\frac{a}{\sqrt{13}}$, mặt khác $\frac{d\left( A;\left( SBC \right) \right)}{d\left( G;\left( SBC \right) \right)}=\frac{AM}{GM}=3$
Vậy $d\left( A;\left( SBC \right) \right)=3d\left( G;\left( SBC \right) \right)=\frac{3a}{\sqrt{13}}$.
| Bài tập 5: Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO=a
a) Tính khoảng cách từ A đến mặt phẳng$\left( SCD \right)$. b) Tính khoảng cách từ trung điểm của SO đến mặt phẳng $\left( SCD \right)$. |
Lời giải chi tiết
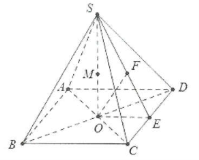
a) Dựng $OE\bot SE,OF\bot SE\Rightarrow d\left( O;\left( SCD \right) \right)\text{=OF}$
Mặt khác
$\text{OE}=\frac{AD}{2}=a\Rightarrow {{d}_{0}}\text{=OF=}\frac{SO.OE}{\sqrt{S{{O}^{2}}+O{{E}^{2}}}}=\frac{a\sqrt{2}}{2}$
Lại có: $\frac{d\left( A;\left( SCD \right) \right)}{d\left( O;\left( SCD \right) \right)}=2\Rightarrow d\left( A;\left( SCD \right) \right)=2{{d}_{o}}=a\sqrt{2}$
b) Gọi M là trung điểm của SO thì
$\frac{d\left( M;\left( SCD \right) \right)}{d\left( O;\left( SCD \right) \right)}=\frac{MS}{OS}=\frac{1}{2}\Rightarrow d\left( M;\left( SCD \right) \right)=\frac{1}{2}{{d}_{o}}=\frac{a\sqrt{2}}{4}$
| Bài tập 6: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh a, biết $\widehat{BAD}=120{}^\circ $ và $SO\bot (ABCD)$. Biết $SO=a\sqrt{3}$, tính khoảng cách từ A đến mặt phẳng $\left( SCD \right)$. |
Lời giải chi tiết
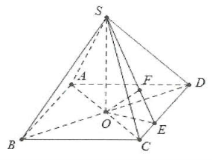
Dựng $OE\bot CD,OF\bot SE\Rightarrow d\left( O;\left( SCD \right) \right)\text{=OF}$
Do $\widehat{BAD}=120{}^\circ \Rightarrow \widehat{CAD}=60{}^\circ \Rightarrow \Delta CAD$ là tam giác đều cạnh a
Khi đó $\widehat{OCE}=60{}^\circ \Rightarrow OE=OC\sin 60{}^\circ =\frac{a}{2}.\frac{\sqrt{3}}{2}=\frac{a\sqrt{3}}{4}$
Do đó $OF=\frac{SO.OE}{\sqrt{S{{O}^{2}}+O{{E}^{2}}}}=\frac{a\sqrt{51}}{17}=d\left( O;\left( SCD \right) \right)$
Mặt khác $\frac{d\left( A;\left( SCD \right) \right)}{d\left( O;\left( SCD \right) \right)}=\frac{AC}{OC}=2$
$\Rightarrow d\left( A;\left( SCD \right) \right)=2OF=\frac{2a\sqrt{51}}{17}$
| Bài tập 7: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, $AB=3AD=3$. Hình chiếu vuông góc của đỉnh S lên mặt phẳng $\left( ABCD \right)$ là điểm $H\in AB$ sao cho $HB=2HA$. Biết $SH=\sqrt{3}$
a) Tính khoảng cách từ B đến mặt phẳng $\left( SAD \right)$. b) Tính khoảng cách từ A đến mặt phẳng $\left( SCD \right)$. |
Lời giải chi tiết
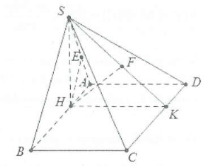
a) $AB=3\Rightarrow HA=1$
Dựng $HE\bot SA$. Ta có: $\left\{ \begin{array} {} AD\bot SH \\ {} AD\bot AB \\ \end{array} \right.\Rightarrow AD\bot HE$
Khi đó $HE\bot \left( SAD \right)\Rightarrow d\left( H;\left( SAD \right) \right)=HE=\frac{HA.SH}{\sqrt{H{{A}^{2}}+S{{H}^{2}}}}=\frac{\sqrt{3}}{2}$
Mặt khác $\frac{{{d}_{B}}}{{{d}_{H}}}=\frac{BA}{HA}=3\Rightarrow d\left( B;\left( SAD \right) \right)=3{{d}_{H}}=\frac{3\sqrt{3}}{2}$
b) Do $AH//CD\Rightarrow AH//\left( SCD \right)\Rightarrow d\left( A;\left( SCD \right) \right)=d\left( H;\left( SCD \right) \right)$
Dựng $HK\bot CD,HF\bot SK\Rightarrow d\left( H;\left( SCD \right) \right)\text{=HF}$
Mặt khác $HK=AD=1,SH=\sqrt{3}\Rightarrow HF=\frac{SH.HK}{\sqrt{S{{H}^{2}}+H{{K}^{2}}}}=\frac{\sqrt{3}}{2}$
Vậy $d\left( A;\left( SCD \right) \right)=\frac{\sqrt{3}}{2}$
| Bài tập 8: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, hình chiếu của đỉnh S trên mặt phẳng đáy trùng với trung điểm của cạnh OA. Biết góc giữa mặt phẳng $\left( SCD \right)$ và đáy bằng $60{}^\circ $. Tính khoảng cách:
a) $d\left( B;\left( SCD \right) \right)$ b) $d\left( A;\left( SBD \right) \right)$ |
Lời giải chi tiết
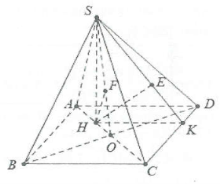
a) Dựng $HK\bot CD\Rightarrow CD\bot \left( SHK \right)$
$\widehat{\left( \left( SCD \right);\left( SHK \right) \right)}=\widehat{SKH}=60{}^\circ $. Ta có: $HK=\frac{3}{4}AD=\frac{3a}{4}$
Mặt khác $SH=HK\tan 60{}^\circ =\frac{3a\sqrt{3}}{4}$
Ta có: $AB//CD\Rightarrow AB//\left( SCD \right)$
Lại có: $\frac{d\left( A;\left( SCD \right) \right)}{d\left( H;\left( SCD \right) \right)}=\frac{AC}{HC}=\frac{4}{3}$
Do đó: $d\left( B;\left( SCD \right) \right)=d\left( A;\left( SCD \right) \right)=\frac{4}{3}d\left( H;\left( SCD \right) \right)$
Dựng $HE\bot SK\Rightarrow HE=HK\sin \widehat{HKE}=HK\sin 60{}^\circ =\frac{3a\sqrt{3}}{8}$
Vậy ![]()
b) Ta có: 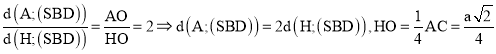
Dựng 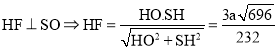
Vậy ![]()
![]()
| Bài tập 9: Cho hình chóp S.ABCD có đáy hình vuông ABCD tâm O, |
Lời giải chi tiết
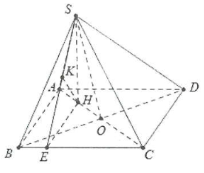
Ta có ∆SBD vuông tại S nên $SO=\frac{1}{2}BD=\frac{1}{2}AC$
$\Rightarrow \vartriangle SAC$ vuông tại S ta có: $S{{A}^{2}}=HA.AC=4H{{A}^{2}}$
$\Leftrightarrow 8{{a}^{2}}=4H{{A}^{2}}\Leftrightarrow HA=a\sqrt{2}\Leftrightarrow AC=4a\sqrt{2}$
$\Rightarrow AB=AC=4a$
Khi đó: $SH=\sqrt{S{{A}^{2}}-H{{A}^{2}}}=a\sqrt{6}$
Do $AD//BC\Rightarrow d\left( D;\left( SBC \right) \right)=d\left( A;\left( SBC \right) \right)$
Mặt khác $\frac{d\left( A;\left( SBC \right) \right)}{d\left( H;\left( SBC \right) \right)}=\frac{AC}{HC}=\frac{4}{3}$
Do đó $d\left( D;\left( SBC \right) \right)=\frac{4}{3}d\left( H;\left( SBC \right) \right)$ . Dựng $HE\bot BC,HK\bot SE\Rightarrow HK\bot \left( SBC \right)$.
Ta có $HE=\frac{3}{4}AB=3a\Rightarrow HK=\frac{HE.SH}{\sqrt{H{{E}^{2}}+S{{H}^{2}}}}=\frac{6a}{\sqrt{10}}\Rightarrow d\left( D;\left( SBC \right) \right)=\frac{4}{3}HK=\frac{8a}{\sqrt{10}}=\frac{4a\sqrt{10}}{5}$
| Bài tập 10: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB là đáy lớn và tam giác ABC là tam giác đều. Các mặt phẳng $\left( SAB \right)$ và $\left( SAC \right)$ cùng vuông góc với đáy, cạnh bên $SC=2a$ và khoảng cách từ C đến mặt phẳng $\left( SAB \right)$ bằng a. Tính khoảng cách từ điểm A đến mặt phẳng (SBC). |
Lời giải chi tiết
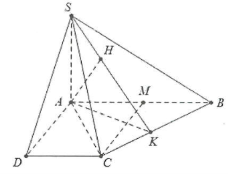
Ta có:$\left\{ \begin{array} {} \left( SAB \right)\bot \left( ABC \right) \\ {} \left( SAC \right)\bot \left( ABC \right) \\ \end{array} \right.\Rightarrow SA\bot (ABC)$
Gọi M là trung điểm của AB suy ra $CM\bot AB\Rightarrow CM\bot \left( SAB \right)$
Do đó $d\left( C;\left( SAB \right) \right)=CM=a$
$\Rightarrow SM=\sqrt{S{{C}^{2}}-C{{M}^{2}}}=a\sqrt{3}$
Gọi K là trung điểm của BC nên $AK=CM=a$
Lại có $CM=\frac{\sqrt{3}}{2}AB\Rightarrow AB=\frac{2a}{\sqrt{3}}$
$\Rightarrow AM=\frac{a}{\sqrt{3}}\Rightarrow SA=\frac{2a\sqrt{6}}{\sqrt{3}}$. Kẻ $AH\bot SK,H\in SK$ nên $AH\bot \left( SBC \right)\Rightarrow d\left( A;\left( SBC \right) \right)=AH$
Khi đó $\frac{1}{A{{H}^{2}}}=\frac{1}{S{{A}^{2}}}+\frac{1}{A{{K}^{2}}}=\frac{1}{{{\left( \frac{2a\sqrt{6}}{3} \right)}^{2}}}+\frac{1}{{{a}^{2}}}\Rightarrow AH=\frac{2a\sqrt{22}}{11}$
| Bài tập 11: Cho hình chóp S.ABCD có đáy là lục giác đều cạnh a. Tam giác SAD vuông cân tại S và thuộc mặt phẳng vuông góc với đáy $\left( ABCD \right)$.
a) Tính khoảng cách từ điểm A đến mặt phẳng (SCD). b) Tính khoảng cách từ điểm B đến mặt phẳng (SCD). |
Lời giải chi tiết
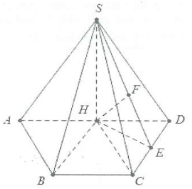
a) Gọi H là trung điểm của AD $\Rightarrow SH\bot AD$
Mặt khác $\left( SAD \right)\bot \left( ABCD \right)$$\Rightarrow SH\bot \left( ABCD \right)$
$\Delta SAD$ vuông cân tại S nên $SH=\frac{AD}{4}=a$
Dễ thấy HC=AB=a$\Rightarrow \Delta HCD$ đều cạnh a
Dựng $HE\bot CD,HF\bot SE\Rightarrow d\left( H;\left( SCD \right) \right)\text{=HF}$
Mặt khác $HE=\frac{a\sqrt{3}}{2}\Rightarrow HF=\frac{SH.HE}{\sqrt{S{{H}^{2}}+H{{E}^{2}}}}=\frac{a\sqrt{21}}{7}$
Do D=2HD$\Rightarrow $$d\left( A;\left( SCD \right) \right)=2HF=\frac{2a\sqrt{21}}{7}$
b) Dễ thấy HDCB là hình thoi cạnh a
Do đó $BH//CD\Rightarrow BD//\left( SCD \right)\Rightarrow d\left( B;\left( SCD \right) \right)=d\left( H;\left( SCD \right) \right)=HF=\frac{a\sqrt{21}}{7}$
| Bài tập 12: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác cân $AC=BC=a,AB=a\sqrt{3}$, hình chiếu vuông góc của A’ lên mặt phẳng đáy trùng với trọng tâm G của tam giác ABC. Biết mặt phẳng $\left( B’C’CB \right)$ tạo với đáy một góc $60{}^\circ $. Tính các khoảng cách:
a) $d\left( A;\left( A’BC \right) \right)$. b) $d\left( C;\left( ABB’A’ \right) \right)$. |
Lời giải chi tiết
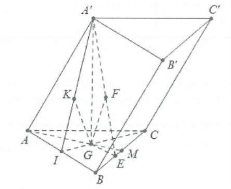
a) Gọi I là trung tâm của AB ta có: $CI\bot AB$
Dựng $GE\bot BC\Rightarrow \left( A’EG \right)\bot BC$
Ta có: $\widehat{A’EG}=60{}^\circ $$\Rightarrow GA’=GE\tan 60{}^\circ $
$CI=\sqrt{B{{C}^{2}}-I{{B}^{2}}}=\frac{a}{2}\Rightarrow CG=\frac{a}{3}$
Mặt khác: $\sin \widehat{ICB}=\frac{\sqrt{3}}{2}\Rightarrow \widehat{ICB}=60{}^\circ $
Khi đó: $GE=CG\sin 60{}^\circ =\frac{a\sqrt{3}}{6}$
$\Rightarrow A’G=GE\tan 60{}^\circ =\frac{a}{2}$
Dựng $GF\bot A’E$ ta có: $GF\bot \left( A’BC \right)\Rightarrow d\left( G;\left( A’BC \right) \right)\text{=GF}$
Ta có: $d\left( A;\left( A’BC \right) \right)=3d\left( G;\left( A’BC \right) \right)=3GF=3GE\sin 60{}^\circ =3\frac{a\sqrt{3}}{6}.\frac{\sqrt{3}}{2}=\frac{3a}{4}$
b) Do $CI=3GI\Rightarrow d\left( C;\left( B’AB \right) \right)=3d\left( G;\left( B’AB \right) \right)$
Dựng $GK\bot A’I\Rightarrow d\left( G;\left( A’AB \right) \right)=\frac{GI.A’G}{\sqrt{G{{I}^{2}}+A'{{G}^{2}}}}$
Trong đó $GI=\frac{1}{3}CI=\frac{a}{6},A’G=\frac{a}{2}\Rightarrow GK=\frac{a\sqrt{10}}{20}\Rightarrow d\left( C;\left( A’AB \right) \right)=\frac{3a\sqrt{10}}{20}$
| Bài tập 13: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, $AB=AD=2a,BC=a$, tam giác SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD), biết cạnh bên $SD=3a$, tính khoảng cách từ A đến mặt phẳng SCD |
Lời giải chi tiết
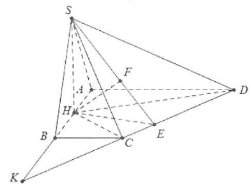
Gọi H là trung điểm của AB ta có: $SH\bot AB$ mặt khác $\left( ABC \right)\bot (ABCD)\Rightarrow SH\bot \left( ABCD \right)$
Ta có: $HD=\sqrt{A{{H}^{2}}+A{{D}^{2}}}=a\sqrt{5}$. Khi đó: $SH=\sqrt{S{{D}^{2}}-H{{D}^{2}}}=2a$
Gọi $K=AB\cap CD\Rightarrow \frac{KB}{KA}=\frac{BC}{AD}=\frac{1}{2}\Rightarrow AK=\frac{4}{3}HK$
Ta có: $d\left( A;\left( SCD \right) \right)=\frac{4}{3}d\left( H;\left( SCD \right) \right)=\frac{4}{3}HF$. Dựng $HE\bot CD,HF\bot SE\Rightarrow HF\bot \left( SCD \right)$
Ta có: $CD=\sqrt{A{{B}^{2}}+{{\left( AD-BC \right)}^{2}}}=a\sqrt{5}$; ${{S}_{HCD}}={{S}_{ABCD}}-{{S}_{HBC}}-{{S}_{HAD}}=3{{a}^{2}}-\frac{3{{a}^{2}}}{2}=\frac{3{{a}^{2}}}{2}$
Do vậy $HE=\frac{2{{S}_{HCD}}}{CD}=\frac{3{{a}^{2}}}{a\sqrt{5}}=\frac{3a}{\sqrt{5}}\Rightarrow HF=\frac{SH.HE}{\sqrt{S{{H}^{2}}+H{{E}^{2}}}}=\frac{6a}{\sqrt{29}}\Rightarrow d\left( A;SCD \right)=\frac{8a}{\sqrt{9}}$.
| Bài tập 14: Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều cạnh a, AD=2a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy, cạnh bên SD tạo với đáy một góc $\varphi $ thỏa mãn $\tan \varphi =\frac{1}{\sqrt{13}}$. Tính khoảng cách từ A đến mặt phẳng SCD. |
Lời giải chi tiết
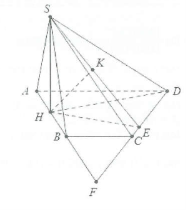
Gọi H là trung điểm của AB ta có: $SH\bot AB$
Mặt khác $\left( SAB \right)\bot \left( ABCD \right)\Rightarrow SH\bot \left( ABCD \right)$
Ta có: $H{{D}^{2}}=A{{H}^{2}}+A{{D}^{2}}-2AD.AH.cos\widehat{HAD}=\frac{{{a}^{2}}}{4}+4{{a}^{2}}-2{{a}^{2}}.cos60{}^\circ =\frac{13{{a}^{2}}}{4}$$\Rightarrow HD=\frac{a\sqrt{13}}{2}$
Ta có: $\widehat{SDH}=\varphi \Rightarrow SH=HD\tan \varphi =\frac{a}{2}$
Gọi $F=AB\cap CD\Rightarrow AF=2AB\Rightarrow \frac{\text{AF}}{HF}=\frac{4}{3}$
Do đó: $d\left( A;\left( SCD \right) \right)=\frac{4}{3}d\left( H;\left( SCD \right) \right)=\frac{4}{3}HK$
Mặt khác $HE=HF\sin 60{}^\circ =\frac{3a}{2}.\frac{\sqrt{3}}{2}=\frac{3a\sqrt{3}}{4}$
$\Rightarrow HK=\frac{HE.SH}{\sqrt{S{{H}^{2}}+H{{E}^{2}}}}=\frac{3a\sqrt{93}}{62}\Rightarrow d\left( A;\left( SCD \right) \right)=\frac{4}{3}HK=\frac{2a\sqrt{93}}{61}$
