Cách tính Khoảng cách giữa đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song
– Khoảng cách giữa đường thẳng và mặt phẳng song song
Khoảng cách giữa đường thẳng a và mặt phẳng $\left( \alpha \right)$ song song với nhau là khoảng cách từ một điểm M bất kì thuộc đường a đến mặt thẳng $\left( \alpha \right)$.
$d\left( a;\left( \alpha \right) \right)=d\left( M;\left( \alpha \right) \right)=MH\left( M\in \left( \alpha \right) \right)$.
– Khoảng cách giữa hai mặt phẳng song song
Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng kia.
$d\left( \left( \alpha \right);\left( \beta \right) \right)=d\left( a;\left( \beta \right) \right)=d\left( A;\left( \beta \right) \right)=AH\left( a\subset \left( \alpha \right),A\in a \right)$
Bài tập tính khoảng cách giữa đường thẳng, mặt phẳng song song có đáp án
| Bài tập 1: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, mặt bên SBC vuông góc với đáy ABC, Gọi M, N, P lần lượt là trung điểm của AB, SA, AC. Tính khoảng cách giữa hai mặt phẳng $\left( MNP \right)$ và $\left( SBC \right)$. |
Lời giải chi tiết
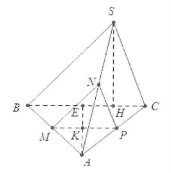
Do $\left\{ \begin{array} {} MP//BC \\ {} MN//SB \\ \end{array} \right.\Rightarrow \left( MNP \right)\bot \left( SBC \right)$
Dựng $SH\bot BC\left( H\in BC \right)$. Mặt khác $\left( SBC \right)\bot \left( ABC \right)$
Do đó $SH\bot \left( ABC \right)$
Gọi M là trung điểm của BC$\Rightarrow AM\bot BC$
Gọi $K=AE\cap MP\Rightarrow KE\bot BC$
Mặt khác $KE\bot SH\Rightarrow KE\bot (SBC)$
Suy ra $d\left( \left( MNP \right);\left( SBC \right) \right)=d\left( K;\left( SBC \right) \right)=KE=\frac{AE}{2}=\frac{a\sqrt{3}}{4}$
| Bài tập 2: Cho hình chóp tứ giác đều S.ABC có cạnh đáy băng 2a và cạnh bên đều bằng $a\sqrt{5}$. Tính khoảng cách giữa đường thẳng CD và mặt phẳng $\left( SAB \right)$. |
Lời giải chi tiết
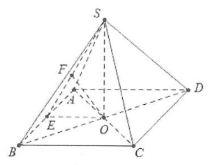
Gọi O là tâm của đáy ABCD$\Rightarrow SO\bot \left( ABCD \right)$
Ta có: $OA=\frac{AC}{2}=a\sqrt{2}$$\Rightarrow SO=\sqrt{S{{A}^{2}}-O{{A}^{2}}}=a\sqrt{3}$
Mặt khác $d\left( CD;\left( SAB \right) \right)=d\left( D;\left( SAB \right) \right)$
Ta có: $\frac{d\left( D;\left( SAB \right) \right)}{d\left( O;\left( SAB \right) \right)}=\frac{DB}{OB}=2$
Dựng $OE\bot AB,\text{OF}\bot \text{SE}$ ta có: $OE=\frac{AD}{2}=a$
Khi đó: $d\left( D;\left( SAB \right) \right)=2OF=2.\frac{SO.OE}{\sqrt{S{{O}^{2}}+O{{E}^{2}}}}=a\sqrt{3}$
| Bài tập 3: Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh bên và cạnh đáy bằng a. Hình chiếu vuông góc của A’ trên $\left( ABC \right)$ trùng với trung điểm của BC.
a) Tính khoảng cách từ AA’ đến các mặt bên $\left( BCC’B’ \right)$ b) Tính khoảng cách giữa hai mặt đáy của lăng trụ. |
Lời giải chi tiết
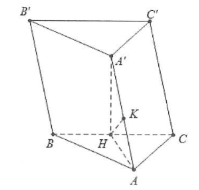
a) Gọi H là trung điểm của BC ta có: $A’H\bot BC$
Do $\Delta \text{ABC}$ đều nên $AH\bot BC\Rightarrow BC\bot \left( A’HA \right)$
Dựng $HK\bot \text{A}A’$ thì $\left\{ \begin{array} {} HK\bot BB’ \\ {} KH\bot BC \\ \end{array} \right.\Rightarrow KH\bot \left( BCC’B’ \right)$
Do đó $d\left( AA’;\left( BCC’B’ \right) \right)=d\left( K;\left( BCC’B’ \right) \right)=KH$
Lại có: $AH=\frac{a\sqrt{3}}{2}\text{,AA}’=a\Rightarrow A’H=\sqrt{A'{{A}^{2}}-A{{H}^{2}}}=\frac{a}{2}$
Suy ra $HK=\frac{\text{AA }\!\!’\!\!\text{ }\text{.AH}}{\text{AA }\!\!’\!\!\text{ }}=\frac{a\sqrt{3}}{4}$
Do đó $d\left( AA’;\left( BCC’B’ \right) \right)=\frac{a\sqrt{3}}{4}$.
b) Ta có: $d\left( \left( ABC \right);\left( A’B’C’ \right) \right)=d\left( A’;\left( ABC \right) \right)=A’H=\frac{a}{2}$
| Bài tập 4: Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy bằng a. Gọi M, N, P lần lượt là trung điểm của AD, DC và A’D’. Tính khoảng cách giữa hai mặt phẳng $\left( MNP \right)$ và $\left( ACC’ \right)$. |
Lời giải chi tiết
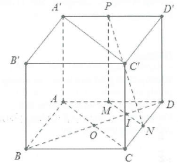
Ta có: $MN//AC,NP//AA’\Rightarrow \left( MNP \right)//\left( ACC’A’ \right)$
Gọi O là tâm hình vuông ABCD và $I=DO\cap MN$
Ta có: $\left\{ \begin{array} {} IO\bot AC \\ {} IO\bot AA’ \\ \end{array} \right.\Rightarrow IO\bot \left( ACC’A’ \right)$
Do đó $d\left( \left( MNP \right);\left( ACC’A’ \right) \right)=d\left( I;\left( ACC’A’ \right) \right)=IO$
Lại có: $IO=\frac{OD}{2}=\frac{BD}{4}=\frac{a\sqrt{2}}{4}$
