Cách Tính khoảng cách giữa hai đường thẳng chéo nhau không vuông góc.
Phương pháp tính khoảng cách:
Dựng đường thẳng chứa a và song song với b (hoặc đường thẳng chứa b và song song với a) để tính khoảng cách giữa hai đường thẳng chéo nhau.
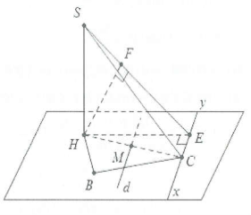
Khảo sát khối chóp đỉnh S có đường cao SH, yêu cầu tính khoảng cách giữa 2 đường thẳng chéo nhau d (thuộc mặt đáy) và đường thẳng SC thuộc mặt bên của khối chóp trong trường hợp d không vuông góc với SC.
Dựng hình:
Tìm giao điểm C của cạnh bên SC và mặt đáy (giao điểm của cạnh thuộc mặt bên và mặt đáy). Từ C ta dựng đường thẳng $\left. xCy \right\|d$
Khi đó d(d;SC) = d(d;(Sxy))
Gọi $M=d\cap HC\Rightarrow d=d(M;(Sxy))$
Ta có : $\frac{d(M;(Sxy))}{d(H;(Sxy))}=\frac{MC}{HC}\Rightarrow d(M;(Sxy))=\frac{MC}{HC}.d(H;(Sxy))$
Chú ý:
Để tính d(d;(Sxy)) ta có thể lấy bất kỳ điểm nào thuộc d (không nhất thiết là điểm M) sao cho việc quy đổi khoảng cách cần tìm về khoảng cách từ chân đường cao H đến mặt phẳng (Sxy) dễ dàng nhất.
Bài tập Tính khoảng cách giữa hai đường thẳng chéo nhau không vuông góc có đáp án chi tiết
| Bài tập 1: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), đáy ABC tam giác vuông tại B có AB = a, $BC=a\sqrt{3}$. Biết $SA=\frac{a}{\sqrt{2}}$
a) Tính khoảng cách giữa hai đường thẳng SB và AC b) Tính khoảng cách giữa hai đường thẳng SC và AB. |
Lời giải chi tiết
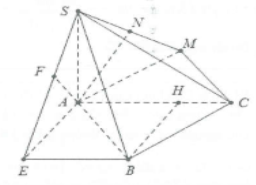
a) Dựng $Bx//AC,AE\bot Bx\Rightarrow (SAE)\bot Bx$
Dựng $AF\bot SE\Rightarrow d(AC;SB)=AF$
Dựng $BH\bot AC$ dễ thấy $AE=BH=\frac{a\sqrt{3}}{2}$
Ta có: $AF=\frac{AE.SA}{\sqrt{S{{A}^{2}}+A{{E}^{2}}}}=\frac{a\sqrt{30}}{10}$
b) Dựng $Cy//AB\Rightarrow d(AB,SC)=d(AB,(SCy))$
Dựng $AM\bot Cy,AN\bot SM\Rightarrow d(AB;(SCy))=AN$
Lại có : $AM=BC=a\sqrt{3}\Rightarrow AN=\frac{AM.SA}{\sqrt{S{{A}^{2}}+A{{M}^{2}}}}=\frac{a\sqrt{21}}{27}$
| Bài tập 2: Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a, hình chiếu vuông góc của B’ lên mặt phẳng đáy trùng với trung điểm H của cạnh AB, góc giữa mặt phẳng (BCC’B’) và mặt phẳng đáy bằng ${{60}^{\circ }}$. Tính khoảng cách giữa 2 đường thẳng AA’ và BC. |
Lời giải chi tiết
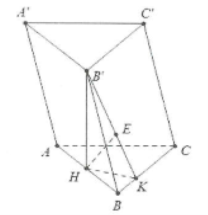
Dựng $HK\bot BC\Rightarrow BC\bot (B’HK)\Rightarrow \overset\frown{B’KH}={{60}^{\circ }}$
Ta có : $HK=HB\sin {{60}^{\circ }}=\frac{a\sqrt{3}}{4}$
$\Rightarrow B’H=HK\tan {{60}^{\circ }}=\frac{3a}{4}$
Do $\text{AA}’//BB’\Rightarrow d(\text{AA}’;BC)=d(\text{AA}’;(B’C’C))$
$d(A;(B’C’CB))=2d(H;(B’C’CB))=2HE$
Ta có : $HE=\frac{HK.B’H}{\sqrt{B'{{H}^{2}}+H{{K}^{2}}}}=\frac{3a}{8}$. Do đó $d=\frac{3a}{4}$
| Bài tập 3: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = AC = 2a, hình chiếu vuông góc của đỉnh S lên mặt phẳng (ABCD) trùng với trung điểm của cạnh AB, biết $SA=a\sqrt{2}$. Tính khoảng cách d giữa 2 đường thẳng SA và BC. |
Lời giải chi tiết
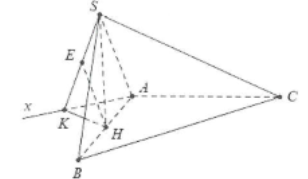
Gọi H là trung điểm của cạnh AB. Khi đó
$SH\bot (ABC)$ và $SH=\sqrt{S{{A}^{2}}-H{{A}^{2}}}=a$
Dựng $Ax//BC\Rightarrow d(SA;BC)=d(B;(SAx))$
Dựng $HK\bot Ax\Rightarrow (SHK)\bot Ax$
Dựng $HE\bot SK\Rightarrow d(B;(SAx))=2d(H;(SAx))$
Ta có : $HK=AH\sin \overset\frown{HAK}=\frac{a}{\sqrt{2}}$
$\Rightarrow d(H;(SAx))=HE=\frac{SH.HK}{\sqrt{S{{H}^{2}}+H{{K}^{2}}}}=\frac{a}{\sqrt{3}}$
Do đó $d(SA;BC)=\frac{2a}{\sqrt{3}}$
| Bài tập 4: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, $AB=a\sqrt{3}$, AC = a, tam giác SBC là tam giác vuông cân đỉnh S và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC). Tính khoảng cách d giữa hai đường thẳng SB và AC. |
Lời giải chi tiết
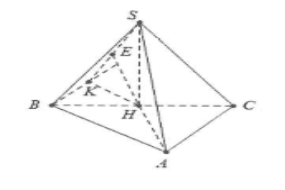
Gọi H là trung điểm của BC. Ta có $SH\bot BC$
Mặt khác $(SBC)\bot (ABC)\Rightarrow SH\bot (ABC)$
Ta có : $BC=\sqrt{A{{B}^{2}}+A{{C}^{2}}}=2a\Rightarrow SH=\frac{1}{2}BC=a$
Dựng $Bx//AC\Rightarrow d(AC;SB)=d(AC;(SBx))$
$=d(C;(SBx))=d$
Dựng : $HK\bot Bx,HE\bot SK\Rightarrow HE\bot (SBx)$
$d(C;(SBx))=2d(H;(SBx))=2HE$
Ta có : $HK=\frac{AB}{2}=\frac{a\sqrt{3}}{2}\Rightarrow HE=\frac{SH.HK}{\sqrt{S{{H}^{2}}+H{{K}^{2}}}}=\frac{a\sqrt{21}}{7}$
Do đó : $d=2d(H;(SBK))=\frac{2a\sqrt{21}}{7}$
| Bài tập 5: Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, $SA\bot (ABCD)$. Gọi M là trung điểm của cạnh CD, biết $SA=a\sqrt{5}$. Tính khoảng cách giữa hai đường thẳng SD và BM |
Lời giải chi tiết
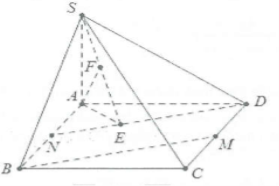
Dựng $\left. DN \right\|BM\Rightarrow N$là trung điểm của AB.
Khi đó $d(SD;BM)=d(BM;(SDN))$
$=d(B;(SDN))=d(A;(SDN))$
Dựng $AE\bot DN\Rightarrow DN\bot (SAE)$, dựng $AF\bot SE$
Khi đó $\left\{ \begin{array} {} AF\bot SE \\ {} AF\bot DN \\ \end{array} \right.\Rightarrow AF\bot (SDN)$
Ta có : $AE=\frac{AN.AD}{\sqrt{A{{N}^{2}}+A{{D}^{2}}}}=\frac{2a}{\sqrt{5}}$
Do vậy $d(B;(SDN))=d(A;(SDN))=AF=\frac{AE.SA}{\sqrt{A{{E}^{2}}+S{{A}^{2}}}}=2a.\sqrt{\frac{5}{29}}=\frac{2a\sqrt{145}}{29}$
| Bài tập 6: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AB = BC = 2a và $SA\bot (ABC)$. Gọi M là trung điểm của AC. Biết góc giữa 2 mặt phẳng (SBC) và (ABC) bằng ${{60}^{\circ }}$. Tính khoảng cách d giữa 2 đường thẳng AB và SM theo a. |
Lời giải chi tiết
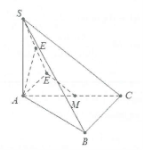
Ta có : $\left\{ \begin{array} {} AB\bot BC \\ {} BC\bot SA \\ \end{array} \right.\Rightarrow BC\bot (SAB)\Rightarrow \overset\frown{SBA}$là góc giữa 2 mặt phẳng (SBC) và (ABC)
Ta có : $SA=AB\tan \overset\frown{SBA}=2a\sqrt{3}$. Dựng Mx//AB
Khi đó $d(AB;SM)=d(AB;(SMx))=d(A;(SMx))$
Dựng $AE\bot Mx;AF\bot SE$khi đó $d(A;(SMx))=AF$
Do AE//BC nên $\overset\frown{EAM}=\overset\frown{ACB}={{45}^{\circ }}$
Suy ra $AE=AMcos{{45}^{\circ }}=a$
Do đó $AF=\frac{SA.AE}{\sqrt{S{{A}^{2}}+A{{E}^{2}}}}=\frac{2a\sqrt{39}}{13}=d$
| Bài tập 7: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, $SA\bot (ABCD)$, đường thẳng SC tạo với đáy góc ${{45}^{\circ }}$. Tính khoảng cách giữa 2 đường thẳng SB và AC |
Lời giải chi tiết
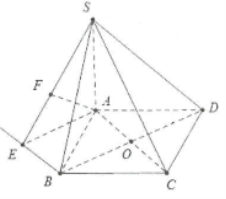
Ta có : $AC=a\sqrt{2};\overset\frown{SCA}=\overset\frown{(SC;(ABCD)}={{45}^{\circ }}$
$\Rightarrow SA=AC=a\sqrt{2}$
Dựng $Bx//AC\Rightarrow d(AC;SB)=d(AC;SBx)$
Dựng $AE\bot Bx,AF\bot SE\Rightarrow d=AF$
Ta có : $BE//AC\Rightarrow BE\bot BD$ dễ dàng suy ra
OEBO là hình chữ nhật suy ra $AE=OB=\frac{a\sqrt{2}}{2}$
$d=\frac{AE.SA}{\sqrt{A{{E}^{2}}+S{{A}^{2}}}}=\frac{a\sqrt{10}}{5}$
| Bài tập 8: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = a, $BC=a\sqrt{3}$. Hình chiếu vuông góc H của đỉnh S lên mặt phẳng (ABCD) là điểm H thỏa mãn $\overrightarrow{HA}=2\overrightarrow{HB}$. Góc giữa mặt phẳng (SCD) và mặt phẳng (ABCD) bằng ${{60}^{\circ }}$. Tính khoảng cách giữa 2 đường thẳng SA và BD. |
Lời giải chi tiết
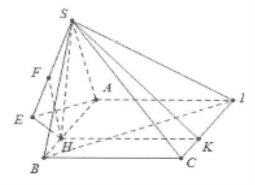
Dựng $HK\bot CD\Rightarrow \overset\frown{SKH}={{60}^{\circ }}$
Ta có : $SH=HK.\tan {{60}^{\circ }}=BC.\tan {{60}^{\circ }}=3a$
Dựng $Ax//BD\Rightarrow d(SA;BD)=d(BD;(SAx))$
$=d(B;(SAx))=\frac{3}{2}d(H;(SAx))$
Dựng $HE\bot Ax,HF\bot SE\Rightarrow d(H;(SAx))=HF$
Ta có : $\tan \overset\frown{ABD}=\sqrt{3}\Rightarrow \overset\frown{HAE}=\overset\frown{ABD}={{60}^{\circ }}$
$\Rightarrow HE=HA.\sin {{60}^{\circ }}=\frac{2a}{3}.\frac{\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}$
Do đó $HF=\frac{SH.HE}{\sqrt{S{{H}^{2}}+H{{E}^{2}}}}=\frac{3a}{2\sqrt{7}}\Rightarrow d(SA;BD)=\frac{9a}{4\sqrt{7}}$
| Bài tập 9: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, $SA\bot (ABCD)$. Biết mặt phẳng (SBC) tạo với đáy một góc ${{60}^{\circ }}$ và M là trung điểm của SD. Tính khoảng cách d giữa 2 đường thẳng AB và CM. |
Lời giải chi tiết
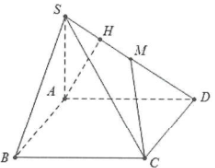
Ta có: $\left\{ \begin{array} {} BC\bot AB \\ {} BC\bot SA \\ \end{array} \right.\Rightarrow BC\bot (SAB)\Rightarrow \overset\frown{SBA}$ là góc giữa 2 mặt phẳng (SBC) và (ABC)
Ta có: $SA=AB\tan \overset\frown{SBA}=a\sqrt{3}$
Do AB//CM do đó d(AB;CM) = d(AB;(CMD))
Dựng $AH\bot SD$khi đó d(A;(SCD)) = AH
Lại có: $AH=\frac{SA.AD}{\sqrt{S{{A}^{2}}+A{{D}^{2}}}}=\frac{a\sqrt{3}}{2}=d(AB;CM)$
| Bài tập 10: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Tính d là khoảng cách giữa 2 đường thẳng AC và C’D. |
Lời giải chi tiết
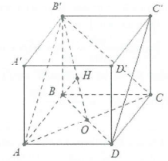
Dễ thấy AB’//C’D do đó
d(AC;C’D) = d(C’D;(ACB’))
Khi đó d = d(D;(B’AC)). Mặt khác OB = OD (với O là tâm hình vuông ABCD)
Khi đó d(D;(B’AC)) = d(B;(B’AC))
Do $\left\{ \begin{array} {} BD\bot AC \\ {} AC\bot BB’ \\ \end{array} \right.\Rightarrow AC\bot (BB’O)$, dựng $BH\bot B’O$
Suy ra $H\bot (B’AC)\Rightarrow h=BH=\frac{BO.BB’}{\sqrt{B{{O}^{2}}+BB{{‘}^{2}}}}=\frac{a}{\sqrt{3}}$
| Bài tập 11: Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là điểm H thuộc đoạn BD sao cho HD = 3HB. Biết góc giữa mặt phẳng (SCD) và mặt phẳng đáy bằng ${{45}^{\circ }}$. Tính khoảng cách giữa 2 đường thẳng SA và BD. |
Lời giải chi tiết
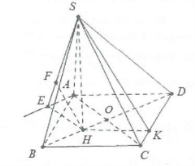
Dựng $HK\bot CD\Rightarrow CD\bot (SHK)$do vậy
$\overset\frown{(SCD;ABCD)}=\overset\frown{SKH}={{45}^{\circ }}$
Ta có: $\Delta $HKD vuông cân tại K do vậy
$HK=KD=\frac{3a}{2}\Rightarrow SH=HK\tan {{45}^{\circ }}=\frac{3a}{2}$
Dựng $Ax//BD$ ta có:
$d(SA;BD)=d(BD;(SAx))=d(H;(SAx))$
Dựng $HE\bot Ax\Rightarrow HE=OA=a\sqrt{2}$
Dựng $HF\bot SE\Rightarrow HF\bot (SAx)$
Ta có: $HF=\frac{SH.HE}{\sqrt{S{{H}^{2}}+H{{E}^{2}}}}=\frac{3a\sqrt{34}}{17}=d(SA;BD)$
| Bài tập 12: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = 2a, $AD=a\sqrt{3}$, cạnh bên SA vuông góc với đáy, gọi M là trung điểm của cạnh CD. Biết SM tạo với mặt phẳng (ABCD) một góc ${{60}^{\circ }}$, tính khoảng cách d giữa 2 đường thẳng AM và SB. |
Lời giải chi tiết
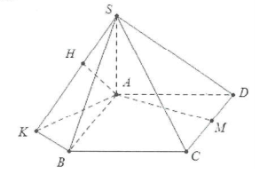
Ta có: $M=\sqrt{A{{D}^{2}}+D{{M}^{2}}}=2a$
$\Rightarrow SA=AM\tan {{60}^{\circ }}=2a\sqrt{3}$
Dựng $Bx//AM\Rightarrow d(AM;SB)=d(A;SBx)$
Dựng $AK\bot Bx,AH\bot SK$
Ta có: $\tan \overset\frown{MAB}=\frac{MD}{AD}=\frac{1}{\sqrt{3}}\Rightarrow \overset\frown{MAD}={{30}^{\circ }}$
$\Rightarrow \overset\frown{BAK}={{30}^{\circ }}\Rightarrow AK=ABcos{{30}^{\circ }}=a\sqrt{3}$
$d(A;(SBx))=AH=a\sqrt{\frac{12}{5}}=\frac{a\sqrt{60}}{5}$
| Bài tập 13: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có $AD=a\sqrt{2}$, hình chiếu vuông góc của đỉnh S xuống mặt đáy là trung điểm của AB, biết tam giác SCD là tam giác vuông tại S và nằm trong mặt phẳng tạo với đáy một góc ${{45}^{\circ }}$. Tính khoảng cách d giữa 2 đường thẳng SA và BD. |
Lời giải chi tiết
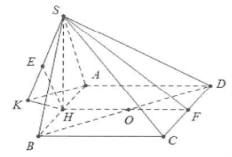
Gọi H là trung điểm của AB. Dựng $HF\bot CD$khi đó $HF=AD=a\sqrt{2}$
Ta có: $CD\bot (SHF)\Rightarrow \overset\frown{SFH}={{45}^{\circ }}$
$\Rightarrow SH=HF\tan {{45}^{\circ }}=a\sqrt{2};SF=HF\sqrt{2}=2a$
Do tam giác SCD vuông cân nên CD = 2SF = 4a
Suy ra $d(A;BD)=\frac{AB.AD}{\sqrt{A{{B}^{2}}+A{{D}^{2}}}}=\frac{4a}{3}$
Dựng $\text{Ax}//BD,HK\bot Ax,HE\bot SK$
Ta có $HK=\frac{1}{2}d(A;BD)=\frac{1}{2}.\frac{4a}{3}=\frac{2a}{3}$. Do vậy $d(SA;BD)=2HE=\frac{4a}{\sqrt{11}}$
| Bài tập 14: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh a, hình chiếu vuông góc của đỉnh S lên mặt phẳng đáy trùng với trọng tâm H của tam giác đều ABC, biết mặt phẳng (SCD) tạo với mặt phẳng (ABCD) một góc ${{60}^{\circ }}$. Tính khoảng cách giữa 2 đường thẳng SA và BD. |
Lời giải chi tiết
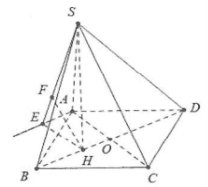
Ta có $\Delta $ABC đều cạnh a nên H là trực tâm của tam giác ABC $\Rightarrow CH\bot AB\Rightarrow CH\bot BC$
$\Rightarrow CD\bot (SHC)\Rightarrow \overset\frown{SCH}={{60}^{\circ }}$
Ta có: $OB=\frac{a\sqrt{3}}{2}\Rightarrow BD=a\sqrt{3}$
$\Rightarrow HB=HC=\frac{a\sqrt{3}}{2}$. Khi đó $SH=\frac{a\sqrt{3}}{2}.\tan {{60}^{\circ }}=a$
Dựng $\text{Ax//BD,HE}\bot \text{Ax},HF\bot SE\Rightarrow HE=OA=\frac{a}{2}$
$d(SA;BD)=HF=\frac{HE.SH}{\sqrt{H{{E}^{2}}+S{{H}^{2}}}}=\frac{a}{\sqrt{5}}$
| Bài tập 15: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông có AB = BC = a,
A’B = $a\sqrt{3}$. Gọi M là trung điểm cạnh BC. Tính theo a khoảng cách giữa hai đường thẳng AM và B’C. |
Lời giải chi tiết
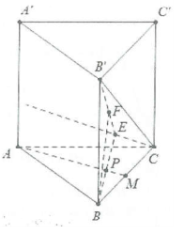
Ta có: $\text{AA}’=\sqrt{A'{{B}^{2}}-A{{B}^{2}}}=a\sqrt{2}$
Dựng $Cx//AM$ khi đó $d(AM;B’C)=d(AM;(B’Cx))$
$=d(M;(B’Cx))=\frac{1}{2}d(B;(B’Cx))$
Dựng $\left\{ \begin{array} {} BE\bot Cx \\ {} BF\bot B’E \\ \end{array} \right.\Rightarrow BF\bot (B’Cx)\Rightarrow d(B;(B’Cx))=BF$
Lại có $BE=2BP$, trong đó $BP=\frac{AB.BM}{\sqrt{A{{B}^{2}}+B{{M}^{2}}}}=\frac{a}{\sqrt{5}}$
Suy ra $BE=\frac{2a}{\sqrt{5}}\Rightarrow BF=\frac{BE.BB’}{\sqrt{B{{E}^{2}}+B{{E}^{2}}}}=\frac{2a}{\sqrt{7}}$
Do đó $d(AM;B’C)=\frac{a}{\sqrt{7}}$
| Ví dụ 16: Cho hình lăng trụ ABC.A’B’C’ có các mặt bên đều là hình vuông cạnh a. Gọi D, E lần lượt là trung điểm của BC, A’C’. Tính khoảng cách giữa các cặp đường thẳng.
a) B’C’ và A’B b) DE và AB’ |
Lời giải
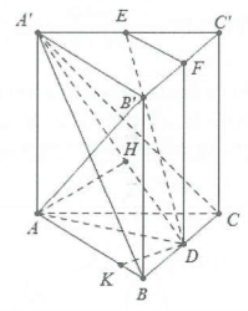
a) Do lăng trụ ABC.A’B’C’ có các mặt bên đều là hình vuông cạnh a. Nên ABC.A’B’C’ là lăng trụ đứng với hai đáy là tam giác đều cạnh a.
Ta có: $B’C’//BC\Rightarrow B’C’//(A’BC)$
$\Rightarrow d(B’C’;A’B)=d(B’C’;(A’BC))=d(B’;(A’BC))$
Gọi $I=A’B\cap AB’\Rightarrow I$là trung điểm của AB’
Khi đó $d(B’;(A’BC))=d(A;(A’BC))$
Dựng $AH\bot A’D\Rightarrow d(A’;(A’BC))=AH=\frac{AA’.AD}{\sqrt{AA{{‘}^{2}}+A{{D}^{2}}}}$
Trong đó $AA’=a;AD=\frac{a\sqrt{3}}{2}\Rightarrow d=AH=\frac{a\sqrt{21}}{7}$
b) Gọi F là trung điểm của B’C’ $\Rightarrow \left\{ \begin{array} {} \text{EF}//A’B’ \\ {} FD//B’B \\ \end{array} \right.\Rightarrow (\text{EFD)//(A }\!\!’\!\!\text{ B }\!\!’\!\!\text{ BA)}\Rightarrow \text{DE//(A }\!\!’\!\!\text{ B }\!\!’\!\!\text{ BA)}$
Khi đó $d(DE;AB’)=d(DE;(A’B’BA))=d(D;(A’B’BA))$
Dựng $DK\bot AB(K\in AB)\Rightarrow d(D;(A’B’BA))=DK=DB\sin \overset\frown{DBK}=\frac{a}{2}\sin {{60}^{\circ }}=\frac{a\sqrt{3}}{4}$
| Ví dụ 17: Cho hình chóp S.ABCD có đáy là hình chữ nhật có AB = a, AD = $a\sqrt{3}$, $SA\bot (ABCD)$. Mặt phẳng (SBC) tạo với đáy một góc ${{60}^{\circ }}$. Gọi M là trung điểm của SA. Tính khoảng cách giữa hai đường thẳng SC và DM |
Lời giải
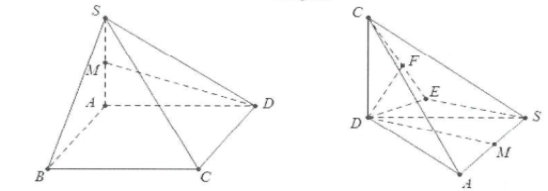
Ta có: $\left\{ \begin{array} {} BC\bot SA \\ {} BC\bot AB \\ \end{array} \right.\Rightarrow BC\bot (SBA)\Rightarrow \overset\frown{(SBC);(ABC))}=\overset\frown{SDB}={{60}^{\circ }}$
Do đó $SA=AB\tan {{30}^{\circ }}=a\sqrt{3}$
Để tính d(SC;DM) ta đổi về đỉnh của hình chóp C.DAS có $CD\bot (SAD)$
Dựng $Sx//DM\Rightarrow d(DM;SC)=d(DM;(CSx))=d(D;(CSx))$
Dựng $DE\bot Sx,DF\bot CE\Rightarrow d(D;(SCx))=DF$
Do $SE//DM\Rightarrow DE=d(S;DM)=d(A;DM)=\frac{AD.AM}{\sqrt{A{{D}^{2}}+A{{M}^{2}}}}=\frac{a\sqrt{3}.\frac{a\sqrt{3}}{2}}{\sqrt{3{{a}^{2}}+\frac{3{{a}^{2}}}{4}}}=\frac{a\sqrt{15}}{5}$
Suy ra $DF=\frac{DE.CD}{\sqrt{C{{D}^{2}}+D{{E}^{2}}}}=\frac{a\sqrt{6}}{4}=d(SC;DM)$
| Ví dụ 18: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, $SA\bot (ABCD)$. Biết AD = 2a, AB = BC = a và SD tạo với đáy một góc ${{30}^{\circ }}$. Gọi K là trung điểm của SD. Tính khoảng cách giữa hai đường thẳng SB và AK. |
Lời giải
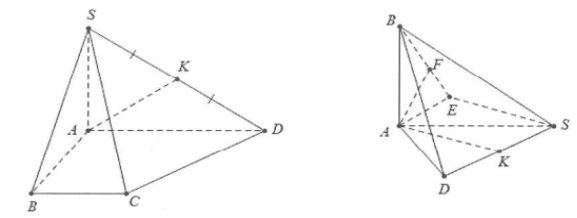
Do $SA\bot (ABCD)\Rightarrow \overset\frown{(SD;(ABCD))}=\overset\frown{SDA}={{30}^{\circ }}\Rightarrow SA=AD\tan {{30}^{\circ }}=\frac{2a}{\sqrt{3}}$
Ta có: $\left\{ \begin{array} {} BA\bot AD \\ {} BA\bot SA \\ \end{array} \right.\Rightarrow BA\bot (SAD)$ ta cắt khối chóp B.SAD có đường cao BA.
Dựng $Sx//AK\Rightarrow d(SB;AK)=d(AK;(SBx))$
Dựng $AE\bot Sx,AF\bot BE\Rightarrow d(AK;(SBx))=d(A;(SBx))=AF$
Do $AK=SK=\frac{1}{2}SD$ và $\overset\frown{ASK}={{90}^{\circ }}-\overset\frown{ADS}={{60}^{\circ }}\Rightarrow \vartriangle SAK$ đều cạnh $\frac{2a}{\sqrt{3}}$
Do đó $AE=d(S;AK)=\frac{SA\sqrt{3}}{2}=a\Rightarrow AF=\frac{AB.AE}{\sqrt{A{{B}^{2}}+A{{E}^{2}}}}=\frac{a\sqrt{2}}{2}$
Vậy $d(SB;AK)=\frac{a\sqrt{2}}{2}$