Bài tập Thể tích khối chóp có đường cao sẵn có – có đáp án chi tiết
Dưới đây là một số bài tập trắc nghiệm thể tích khối chóp có đường cao
| Bài tập 1: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy, đường thẳng SC tạo với đáy một góc $60{}^\circ $. Thể tích khối chóp S.ABC bằng?
A. $\frac{{{a}^{3}}}{8}$. B. $\frac{{{a}^{3}}}{4}$. C. $\frac{{{a}^{3}}}{2}$. D. $\frac{3{{a}^{3}}}{4}$. |
Lời giải chi tiết:
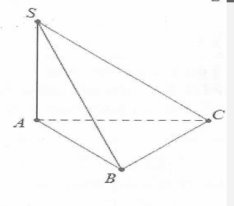
Chú ý: Nếu tam giác ABC đều cạnh a thì độ dài đường trung tuyến
bằng m = $\frac{a\sqrt{3}}{2}$
Ta có: $SA\bot (ABC)\Rightarrow \widehat{(SC;(ABC))}=\widehat{SCA}=60{}^\circ $
$\begin{array} {} \Rightarrow \tan 60{}^\circ =\frac{SA}{\text{A}C}\Rightarrow SA=AC\tan 60{}^\circ =a\sqrt{3},{{S}_{ABC}}=\frac{{{a}^{2}}\sqrt{3}}{4} \\ {} \Rightarrow V=\frac{1}{3}SA.{{S}_{ABC}}=\frac{1}{3}a\sqrt{3}.\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{{{a}^{3}}}{4} \\ \end{array}$
Chọn B
| Bài tập 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trung điểm của cạnh AD, cạnh bên SB hợp với đáy một góc $60{}^\circ $. Tính theo a thể tích V của khối chóp S.ABCD
A. V $=\frac{{{a}^{3}}\sqrt{15}}{2}$. B. V $=\frac{{{a}^{3}}\sqrt{15}}{6}$. C. V $=\frac{{{a}^{3}}\sqrt{5}}{4}$. D. V $=\frac{{{a}^{3}}\sqrt{15}}{18}$. |
Lời giải chi tiết
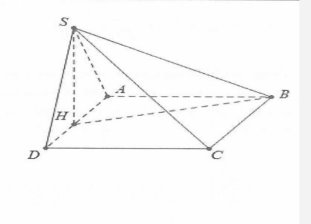
| Gọi H là trung điểm của $AD\Rightarrow AH\bot (ABCD)$
Ta có: $BH=\sqrt{{{\left( \frac{a}{2} \right)}^{2}}+{{a}^{2}}}=\frac{a\sqrt{5}}{2}$$\begin{array} {} SH=BH\tan 60{}^\circ =\frac{a\sqrt{5}}{2}.\sqrt{3}=\frac{a\sqrt{15}}{2} \\ {} {{V}_{S.ABCD}}=\frac{1}{3}SH.{{S}_{ABCD}}=\frac{1}{3}.\frac{a\sqrt{15}}{2}.{{a}^{2}}=\frac{{{a}^{3}}\sqrt{15}}{6} \\ \end{array}$ Chọn B. |
| Bài tập 3: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, $SA\bot (ABC)$. Biết mặt phẳng $(SBC)$ tạo với đáy một góc $60{}^\circ $. Thể tích khối chóp S.ABC là
A. $\frac{{{a}^{3}}\sqrt{3}}{24}$. B. $\frac{{{a}^{3}}\sqrt{3}}{8}$. C. $\frac{{{a}^{3}}\sqrt{3}}{6}$. D.$\frac{{{a}^{3}}\sqrt{3}}{18}$. |
Lời giải chi tiết:
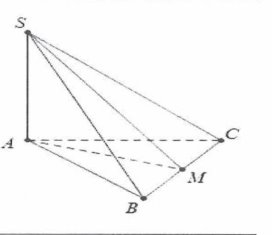
| Gọi M là trung điểm của $BC\Rightarrow AM\bot BC$ và$AM=\frac{a\sqrt{3}}{2}.$
Lại có: $BC\bot SA\Rightarrow BC\bot (SMA)\Rightarrow \widehat{((SBC);(ABC))}=\widehat{SMA}=60{}^\circ $. Khi đó $SA=AM\tan 60{}^\circ =\frac{3a}{2},{{S}_{ABC}}=\frac{{{a}^{2}}\sqrt{3}}{4}.$ Thể tích khối chóp là:$V=\frac{1}{4}SA.{{S}_{ABC}}=\frac{{{a}^{3}}\sqrt{3}}{8}$. Chọn B. |
| Bài tập 4: Cho hình chóp S.ABC có đáy là tam giác vuông tại B có AB=a, BC=$a\sqrt{3}$. Hình chiếu của đỉnh S trên mặt phẳng đáy trùng với trung điểm của cạnh AC. Biết SB tạo với đáy một góc $30{}^\circ $. Thể tích khối chóp S.ABC là:
A. $\frac{{{a}^{3}}}{2}$. B. $\frac{{{a}^{3}}}{4}$. C. $\frac{{{a}^{3}}\sqrt{3}}{6}$. D. $\frac{{{a}^{3}}}{6}$. |
Lời giải chi tiết:
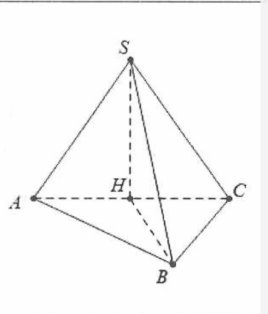
Gọi H là trung điểm của $AC\Rightarrow AH\bot (ABC).$
Khi đó $\widehat{(SB);(ABC))}=\widehat{SBH}.$ Ta có:$AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=2a.$
Tam giác ABC có đường trung tuyến BH ứng với cạnh huyền nên
$BH=\frac{AC}{2}=a.$Do $\widehat{SBH}=30{}^\circ \Rightarrow SH=HB\tan 30{}^\circ =\frac{a}{\sqrt{3}}.$
Lại có: ${{S}_{ABC}}=\frac{1}{2}BA.BC=\frac{{{a}^{2}}\sqrt{3}}{2}$
Suy ra: ${{V}_{S.ABC}}=\frac{1}{3}SH.{{S}_{ABC}}=\frac{1}{3}.\frac{a}{\sqrt{3}}.\frac{{{a}^{2}}\sqrt{3}}{2}=\frac{{{a}^{3}}}{6}.$Chọn D
| Bài tập 5: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB= 2a, AD=$a\sqrt{3}$, cạnh bên SA vuông góc với đáy, gọi M là trung điểm của cạnh CD. Biết SM tạo với mặt phẳng (ABCD) một góc $60{}^\circ $, tính thể tích V của khối chóp S.ABCD.
A. V= $2{{a}^{3}}$. B. V=$4{{a}^{3}}\sqrt{3}$. C. V=$12{{a}^{3}}$. D. V=$4{{a}^{3}}$. |
Lời giải chi tiết:
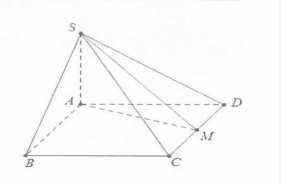
| Do $SA\bot (ABCD)\Rightarrow \widehat{(SM;(ABCD))}=\widehat{SMA}=60{}^\circ .$
Ta có: $AM=\sqrt{A{{D}^{2}}+D{{M}^{2}}}=2a$ $\Rightarrow SA=AM\tan 60=2a\sqrt{3}$. Mặt khác ${{S}_{ABCD}}=AB.AD=2{{a}^{2}}\sqrt{3}$. ${{V}_{S}}_{.ABCD}=\frac{1}{3}.2a\sqrt{3}.2{{a}^{2}}\sqrt{3}=4{{a}^{3}}$. Chọn D. |
| Bài tập 6: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt đáy, SD tạo với mặt phẳng (SAB) một góc bằng $30{}^\circ $.Tính thể tích V của khối chóp S.ABCD.
A. V= $\frac{\sqrt{6}{{a}^{3}}}{18}$. B. V=$\sqrt{3}{{a}^{3}}$. C. V= $\frac{\sqrt{6}{{a}^{3}}}{3}$ D. V=$\frac{\sqrt{3}{{a}^{3}}}{3}$. |
Lời giải chi tiết:
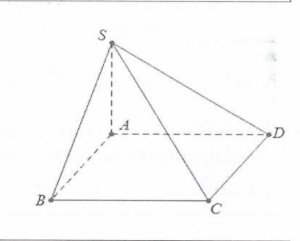
Ta có: $\left\{ \begin{array} {} AD\bot AB \\ {} AD\bot SA \\ \end{array} \right.\Rightarrow AD\bot (SAB)$
Khi đó: $\left( \widehat{SD;(SAB)} \right)=\widehat{DSA}=30{}^\circ $suy ra
$SA\tan 30{}^\circ =AD\Rightarrow SA=a\sqrt{3}$
Do đó ${{V}_{S.}}_{ABCD}=\frac{1}{3}SA.{{S}_{ABCD}}=\frac{{{a}^{3}}\sqrt{3}}{3}$. Chọn D.
| Bài tập 7: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có AB= 2a. Hình chiếu vuông góc của đỉnh S xuống mặt đáy là trung điểm của AB. Biết rằng SA= $a\sqrt{7}$ và mặt phẳng (SCD) tạo với đáy một góc $60{}^\circ $. Thể tích khối chóp là:
A. $\frac{4{{a}^{3}}\sqrt{6}}{3}$. B. $\frac{2{{a}^{3}}\sqrt{3}}{3}$. C. $\frac{2{{a}^{3}}\sqrt{6}}{3}$. D. $\frac{4{{a}^{3}}\sqrt{3}}{3}$. |
Lời giải chi tiết:
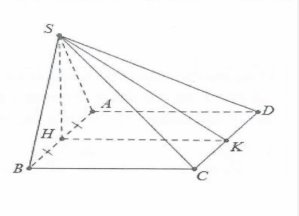
| Ta có: $SH=\sqrt{S{{A}^{2}}-H{{A}^{2}}}=a\sqrt{6}$.
Dựng $HK\bot CD$ ta có: $\left\{ \begin{array} {} HK\bot CD \\ {} SH\bot CD \\ \end{array} \right.$ Suy ra $CD\bot (SHK)\Rightarrow \widehat{SKH}=60{}^\circ $. Khi đó $HK\tan 60{}^\circ =SH\Rightarrow HK=\frac{a\sqrt{6}}{\sqrt{3}}=a\sqrt{2}=AD$. Khi đó ${{S}_{ABCD}}=2{{a}^{2}}\sqrt{2}\Rightarrow V=\frac{1}{3}SH.{{S}_{ABCD}}=\frac{4{{a}^{3}}\sqrt{3}}{3}$. Chọn D. |
| Bài tập 8: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B có AD = 2AB= 2CD= 2a và $SA\bot (ABCD)$. Biết SA tạo với (SCD) một góc $30{}^\circ $. Thể tích khối chóp $S.ABCD$ là:
A. $\frac{{{a}^{3}}\sqrt{6}}{6}$. B. $\frac{{{a}^{3}}\sqrt{6}}{3}$. C. $\frac{{{a}^{3}}\sqrt{3}}{3}$. D.$\frac{{{a}^{3}}\sqrt{6}}{2}$. |
Lời giải chi tiết:
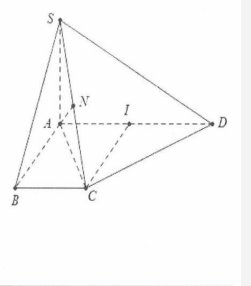
Ta có: $AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=a\sqrt{2}$
Gọi I là trung điểm của $AD\Rightarrow ABCI$là hình vuông cạnh $a\Rightarrow CI=\frac{AD}{2}=a\Rightarrow \Delta ACD$ vuông tại C.
Khi đó: $\left\{ \begin{array} {} CD\bot SA \\ {} CD\bot AC \\ \end{array} \right.\Rightarrow CD\bot (SAC)$.
Dựng $AN\bot SC\Rightarrow \left( \widehat{SA;(SCD)} \right)=\widehat{ASN}=\widehat{ASC}=30{}^\circ $.
Suy ra $SA=AC\cot 30{}^\circ =a\sqrt{6}$.
Lại có: ${{S}_{ABCD}}=\frac{AD+BC}{2}.AB=\frac{3{{a}^{2}}}{2}$.
Do đó ${{V}_{S.ABCD}}=\frac{1}{3}SA.{{S}_{ABCD}}=\frac{{{a}^{3}}\sqrt{6}}{2}$. Chọn D.
| Bài tập 9: Cho khối chóp S.ABCD có đáy là hình vuông có cạnh a, SA vuông góc với đáy và SC tạo với mặt phẳng (SAB) một góc $30{}^\circ $. Tính thể tích V của khối chóp đã cho.
A. V= $\frac{\sqrt{6}{{a}^{3}}}{3}$. B. V= $\frac{2{{a}^{3}}}{3}$. C. V= $\sqrt{2}{{a}^{3}}$. D. V= $\frac{\sqrt{2}{{a}^{3}}}{3}$. |
Lời giải chi tiết:
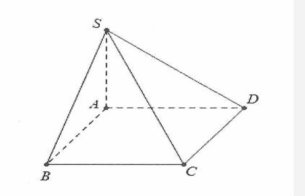
Ta có: $\left\{ \begin{array} {} BC\bot AB \\ {} BC\bot SA \\ \end{array} \right.\Rightarrow BC\bot (SAB)$
Do đó $\left( \widehat{SC;(SAB)} \right)=\widehat{SCB}=30{}^\circ $
Khi đó: $SB=BC.\cot 30{}^\circ =a\sqrt{3}\Rightarrow SA=\sqrt{S{{B}^{2}}-A{{B}^{2}}}=a\sqrt{2}$
Mặt khác ${{S}_{ABCD}}={{a}^{2}}\Rightarrow $ ${{V}_{S.ABCD}}=\frac{{{a}^{3}}\sqrt{2}}{3}$. Chọn D.
| Bài tập 10: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh a, hình chiếu vuông góc của đỉnh S lên mặt phẳng đáy trùng với tâm H của tam giác đều ABC, biết mặt phẳng (SDC) tạo với mặt phẳng (ABCD) một góc $60{}^\circ $. Thể tích khối chóp S.ABCD là:
A.$\frac{{{a}^{3}}\sqrt{3}}{6}$. B. $\frac{{{a}^{3}}\sqrt{3}}{6}$. C.$\frac{{{a}^{3}}}{6}$. D.$\frac{{{a}^{3}}\sqrt{3}}{12}$. |
Lời giải chi tiết:
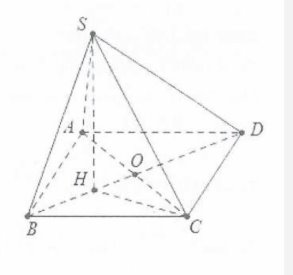
Ta có $\Delta ABC$ đều cạnh a nên H là trực tâm của tam giác $ABC\Rightarrow CH\bot AB\Rightarrow CH\bot BC$
$\Rightarrow CD\bot (SHC)\Rightarrow \widehat{SCH}=60{}^\circ $.
Ta có: $OB=\frac{a\sqrt{3}}{2}\Rightarrow BD=a\sqrt{3}\Rightarrow HB=HC=\frac{2}{3}OB=\frac{a\sqrt{3}}{3}$.
Khi đó:$SH=\frac{a\sqrt{3}}{3}.\tan 60{}^\circ =a,{{S}_{ABCD}}=2{{S}_{ABC}}=\frac{{{a}^{2}}\sqrt{3}}{2}$
${{V}_{S.ABCD}}=\frac{1}{3}.a.\frac{{{a}^{2}}\sqrt{3}}{2}=\frac{{{a}^{3}}\sqrt{3}}{6}$. Chọn A.
| Bài tập 11: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), đáy ABC tam giác vuông tại B có AB= a, BC=$a\sqrt{3}$, biết góc giữa hai mặt phẳng (SAC) và (SBC) bằng $60{}^\circ $. Tính thể tích khối chóp S.ABC.
A.. $\frac{{{a}^{3}}\sqrt{6}}{12}$. B. $\frac{{{a}^{3}}\sqrt{6}}{4}$. C.$\frac{{{a}^{3}}\sqrt{2}}{12}$. D.$\frac{{{a}^{3}}\sqrt{6}}{8}$. |
Lời giải chi tiết:
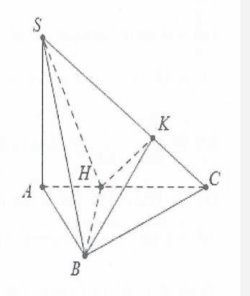
Dựng $BH\bot AC\Rightarrow BH\bot (SAC)$
Dựng $HK\bot SC\Rightarrow (HKB)\bot SC\Rightarrow \widehat{HKB}=60{}^\circ $.
Ta có: $BH=\frac{a\sqrt{3}}{2}\Rightarrow BK\sin 60{}^\circ =\frac{a\sqrt{3}}{2}\Rightarrow BK=a$.
Do $\left\{ \begin{array} {} BC\bot AB \\ {} BC\bot SA \\ \end{array} \right.\Rightarrow BC\bot SB$. Khi đó $\Delta SBC$vuông tại B nên ta có:
$\frac{1}{S{{B}^{2}}}+\frac{1}{B{{C}^{2}}}=\frac{1}{B{{K}^{2}}}\Rightarrow SB=a\sqrt{\frac{3}{2}}\Rightarrow SA=\sqrt{S{{B}^{2}}-A{{B}^{2}}}=\frac{a}{\sqrt{2}}$
${{V}_{S.ABCD}}=\frac{1}{3}.\frac{a}{\sqrt{2}}.\frac{1}{2}{{a}^{2}}\sqrt{3}=\frac{{{a}^{3}}\sqrt{6}}{12}$. Chọn A.
| Bài tập 12: Cho hình chóp tứ giác S.ABCD có đáy là hình vuông ABCD tâm O cạnh 4a, M là một điểm thuộc cạnh AB sao cho MA=3MB, hình chiếu vuông góc của H lên mặt phẳng (ABCD) là trung điểm của cạnh OM. Biết góc giữa hai mặt phẳng (SBC) và đáy là $60{}^\circ $. Thể tích khối chóp S.ABCD là:
A. $4{{a}^{3}}\sqrt{3}$. B.$\frac{8\sqrt{3}}{3}{{a}^{3}}$. C.$8{{a}^{3}}\sqrt{3}$. D.$4{{a}^{3}}$. |
Lời giải chi tiết:
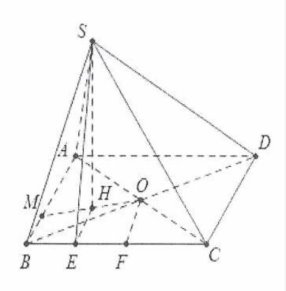
Dựng $HE\bot BC,OF\bot BC$
Ta có $(SHE)\bot BC\Rightarrow \widehat{SEH}=60{}^\circ $
Mặt khác ME là đường trung bình của hình thang MOFB $\Rightarrow ME=\frac{MB+OF}{2}=\frac{3a}{2}$
Ta có: $SH=HE.\tan 60{}^\circ =\frac{3a\sqrt{3}}{2}$.
V$_{S.ABCD}=\frac{1}{3}.\frac{3a\sqrt{3}}{2}.16{{a}^{2}}=8{{a}^{3}}\sqrt{3}$. Chọn C.
| Bài tập 13: Cho hình chóp S.ABCD có đáy là nửa lục giác đều cạnh a, AD= 2a, $SA\bot (ABCD)$. Mặt phẳng $(SCD)$tạo với đáy một góc $45{}^\circ $. Thể tích khối chóp S.ACD là:
A.$\frac{{{a}^{3}}}{2}$ . B. $\frac{{{a}^{3}}}{4}$. C. $\frac{3{{a}^{3}}}{4}$ . D.${{a}^{3}}$. |
Lời giải chi tiết:
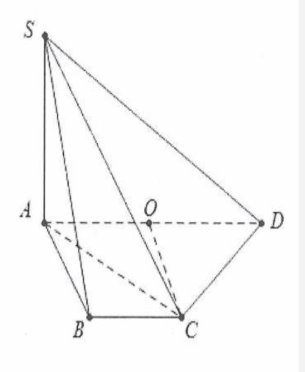
| Gọi O là trung điểm của AD dễ thấy $OC=AB=a=\frac{1}{2}AD\Rightarrow \Delta ACD$ vuông tại C
Khi đó $\left\{ \begin{array} {} CD\bot AC \\ {} CD\bot SA \\ \end{array} \right.\Rightarrow CD\bot (SAC)$ Do vậy $\widehat{SCA}=45{}^\circ $. Lại có tam giác ACD vuông tại C nên $AC=\sqrt{A{{D}^{2}}-C{{D}^{2}}}=a\sqrt{3}\Rightarrow SA=a\sqrt{3}.\tan 45{}^\circ =a\sqrt{3}$ Ta có: $d(C;AD)=CD\sin \widehat{CDA}=CD.\sin 60{}^\circ =\frac{a\sqrt{3}}{2}$. Do đó ${{S}_{ABCD}}=\frac{AD+BC}{2}.\frac{a\sqrt{3}}{2}=\frac{3{{a}^{2}}\sqrt{3}}{4}$ Vậy ${{V}_{S.ABCD}}=\frac{1}{3}SA.{{S}_{ABCD}}=\frac{3{{a}^{3}}}{4}$. Chọn C. |
