Cách giải bài toán tính Thể tích một số khối chóp đặc biệt
Khối chóp có các cạnh bên bằng nhau
Cho khối chóp $S.{{A}_{1}}{{A}_{2}}…{{A}_{n}}$ có tất cả các cạnh bên bằng nhau: $S{{A}_{1}}=S{{A}_{2}}=…=S{{A}_{n}}$.
Dựng đường cao $SH\bot \left( {{A}_{1}}{{A}_{2}}{{A}_{n}} \right)$ của khối chóp.
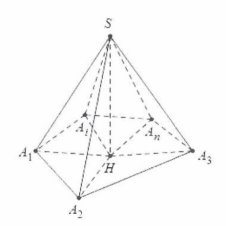
Khi đó theo định lý Pytago ta có:
$S{{H}^{2}}=S{{A}_{1}}^{2}-H{{A}_{1}}^{2}=S{{A}_{2}}^{2}-H{{A}_{2}}^{2}=….=S{{A}_{n}}^{2}-H{{A}_{n}}^{2}$.
Lại có $S{{A}_{1}}=S{{A}_{2}}=…=S{{A}_{n}}$ suy ra $H{{A}_{1}}=H{{A}_{2}}=…=H{{A}_{n}}$.
Như vậy: Hình chiếu vuông góc của đỉnh S xuống mặt đáy trùng với tâm đường tròn ngoại tiếp của đa giác ${{A}_{1}}{{A}_{2}}…{{A}_{n}}$.
Khi đó $SH=h={{R}_{}}\tan \alpha $.
Khối chóp có các cạnh bên tạo với đáy các góc bằng nhau
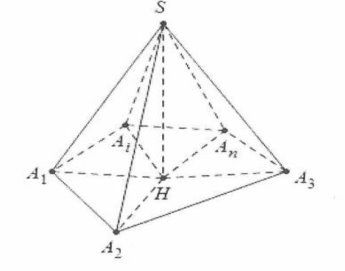
Cho khối chóp $S.{{A}_{1}}{{A}_{2}}…{{A}_{n}}$ có tất cả các cạnh bên đều tạo với đáy một góc $\alpha $.
Dựng đường cao $SH\bot \left( {{A}_{1}}{{A}_{2}}{{A}_{n}} \right)$ của khối chóp.
Khi đó: $\widehat{S{{A}_{1}}H}=\widehat{S{{A}_{2}}H}=….=\widehat{S{{A}_{n}}H}=\alpha $suy ra
$SH=H{{A}_{1}}\tan \alpha =H{{A}_{2}}\tan \alpha =….=H{{A}_{n}}\tan \alpha $.
Do đó $H{{A}_{1}}=H{{A}_{2}}=…=H{{A}_{n}}$ suy ra hình chiếu vuông góc của đỉnh S xuống mặt đáy trùng với tâm đường tròn ngoại tiếp của đa giác ${{A}_{1}}{{A}_{2}}…{{A}_{n}}$.
Khi đó $SH=h={{R}_{}}\tan \alpha $.
Khối chóp có các mặt bên đều tạo với đáy các góc bằng nhau
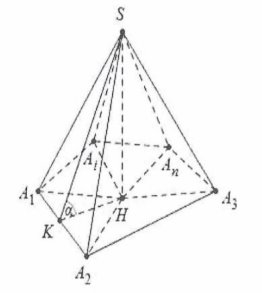
| Cho khối chóp $S.{{A}_{1}}{{A}_{2}}…{{A}_{n}}$ có tất cả các mặt bên đều tạo với đáy một góc$\alpha $
Dựng đường cao $SH\bot \left( {{A}_{1}}{{A}_{2}}{{A}_{n}} \right)$ của khối chóp. Dựng $H{{K}_{1}}\bot {{A}_{1}}{{A}_{2}}$,$H{{K}_{2}}\bot {{A}_{2}}{{A}_{3}}$,… ,$H{{K}_{n}}\bot {{A}_{n}}{{A}_{1}}$ Do $\left\{ \begin{array} {} H{{K}_{1}}\bot {{A}_{1}}{{A}_{2}} \\ {} {{A}_{1}}{{A}_{2}}\bot SH \\ \end{array} \right.\Rightarrow {{A}_{1}}{{A}_{2}}\bot \left( S{{K}_{1}}H \right)\Rightarrow \widehat{S{{K}_{1}}H}=\alpha $. Tương tự như vậy ta có: $\overset\frown{S{{K}_{1}}H}=\overset\frown{S{{K}_{2}}H}=….=\overset\frown{S{{K}_{n}}H}=\alpha $. Suy ra $SH=H{{K}_{1}}\tan \alpha =H{{K}_{2}}\tan \alpha ….=H{{K}_{n}}\tan \alpha $ do đó $H{{K}_{1}}=H{{K}_{2}}=…=H{{K}_{n}}$. Suy ra điểm H trùng với tâm đường tròn tiếp xúc với tất cả các cạnh (hay đường tròn nội tiếp) của đa giác${{A}_{1}}{{A}_{2}}…{{A}_{n}}$. Khi đó $SH=h={{r}_{}}\tan \alpha $. |
Bài tập trắc nghiệm tính thể tích khối chóp đặc biệt có đáp án chi tiết
| Bài tập 1: Cho hình chóp S.ABC có đáy là tam giác ABC, các cạnh bên SA=SB=SC= $a$. Biết rằng $\widehat{ASB}=\widehat{BSC}=60{}^\circ $, $\widehat{ASC}=90{}^\circ $. Thể tích khối chóp đã cho là:
A.V= $\frac{{{a}^{3}}\sqrt{3}}{6}$. B. V= $\frac{{{a}^{3}}\sqrt{2}}{6}$. C. V= $\frac{{{a}^{3}}\sqrt{2}}{12}$. D.V=$\frac{{{a}^{3}}\sqrt{3}}{12}$. |
Lời giải chi tiết:
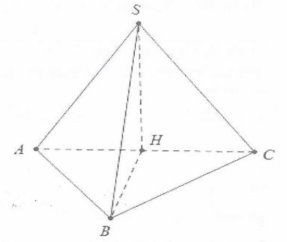
| Dễ thấy các tam giác ASB, BSC là tam giác đều do đó AB = BC =$a$.
Mặt khác:$AC=\sqrt{S{{A}^{2}}+S{{C}^{2}}}=a\sqrt{2}=\sqrt{A{{B}^{2}}+B{{C}^{2}}}$ Do đó tam giác ABC vuông tại B. Mặt khác SA = SB = SC =$a$ nên hình chiếu vuông góc của đỉnh S xuống mặt đáy là tâm đường tròn ngoại tiếp tam giác ABC và là trung điểm của cạnh huyền AC. Ta có: $SH=\frac{a\sqrt{2}}{2}$; ${{S}_{ABC}}=\frac{{{a}^{2}}}{2}$$\Rightarrow $${{V}_{S.ABC}}=\frac{{{a}^{3}}\sqrt{2}}{12}$. Chọn C. |
| Bài tập 2: Cho hình chóp S.ABC có đáy là tam giác ABC, các cạnh bên SA=SB=SC= $a$. Biết rằng $\widehat{ASB}=60{}^\circ $,$\widehat{BSC}=90{}^\circ $, $\widehat{ASC}=120{}^\circ $. Thể tích khối chóp đã cho là:
A.V= $\frac{{{a}^{3}}\sqrt{3}}{6}$. B. V= $\frac{{{a}^{3}}\sqrt{2}}{6}$. C. V= $\frac{{{a}^{3}}\sqrt{2}}{12}$. D.V=$\frac{{{a}^{3}}\sqrt{3}}{12}$. |
Lời giải chi tiết:
| Tam giác SAB đều nên AB=$a$ , $\Delta $SBC vuông tại S nên $BC=\sqrt{S{{B}^{2}}+S{{C}^{2}}}=a\sqrt{2}$.
Mặt khác $AC=\sqrt{S{{A}^{2}}+S{{C}^{2}}-2SA.SC\cos \widehat{ASC}}=a\sqrt{3}$ Do $A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}$nên tam giác ABC vuông tại B. Mặt khác SA=SB=SC= $a$ nên hình chiếu vuông góc của đỉnh S xuống mặt đáy là tâm đường tròn ngoại tiếp tam giác ABC và là trung điểm của cạnh huyền AC. Ta có: ${{S}_{ABC}}=\frac{{{a}^{2}}\sqrt{2}}{2}$, $SH=\sqrt{S{{A}^{2}}-H{{A}^{2}}}=\frac{a}{2}$. $\Rightarrow $${{V}_{S.ABC}}=\frac{1}{3}SH.{{S}_{ABC}}=\frac{{{a}^{3}}\sqrt{2}}{12}$. Chọn C. |
| Bài tập 3: Cho hình chóp S.ABC có đáy là tam giác ABC, có AB=AC= $a$, $\widehat{BAC}=120{}^\circ $. Các cạnh bên đều tạo với đáy một góc $60{}^\circ $.Thể tích khối chóp S.ABC là:
A.V= $\frac{{{a}^{3}}}{4}$ . B. V=$\frac{{{a}^{3}}\sqrt{3}}{4}$ . C. V=$\frac{{{a}^{3}}\sqrt{3}}{8}$. D.V=$\frac{{{a}^{3}}\sqrt{3}}{12}$. |
Lời giải chi tiết:
Diện tích tam giác ABC là: ${{S}_{ABC}}=\frac{1}{2}AB.AC.\sin \widehat{BAC}=\frac{{{a}^{2}}\sqrt{3}}{4}$.
Do các cạnh bên đều tạo với đáy một góc bằng $60{}^\circ $$\Rightarrow $ hình chiếu vuông góc của đỉnh S xuống mặt đáy là tâm đường tròn ngoại tiếp tam giác ABC.
Lại có:$BC=\sqrt{A{{B}^{2}}+A{{C}^{2}}-2AB.AC\cos \widehat{BAC}}=a\sqrt{3}\Rightarrow {{R}_{ABC}}=\frac{BC}{2\sin A}=\frac{a\sqrt{3}}{2\sin 120{}^\circ }=a$.
Suy ra $SH={{R}_{ABC}}.\tan 60{}^\circ =a\sqrt{3}$$\Rightarrow $${{V}_{S.ABC}}=\frac{1}{3}SH.{{S}_{ABC}}=\frac{{{a}^{3}}}{4}$. Chọn A.
| Bài tập 4: Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B có AB = 3, BC = 4. Biết rằng các mặt bên của khối chóp đều tạo với đáy một góc bằng nhau và bằng $60{}^\circ $. Thể tích khối chóp đã cho là
A.V= $\frac{5\sqrt{3}}{3}$ . B. V=$\frac{5\sqrt{3}}{6}$ . C. V=$\frac{5\sqrt{3}}{2}$. D.V=$\frac{5\sqrt{3}}{12}$. |
Lời giải chi tiết:
| Ta có: H là tâm đường tròn nội tiếp tam giác ABC.
Lại có $p.r={{S}_{ABC}}$. Trong đó ${{S}_{ABC}}=\frac{1}{2}AB.BC=6$;$AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=5$ Suy ra $p=\frac{AB+BC+CA}{2}=6\Rightarrow r=\frac{5}{6}=HK$. Khi đó $SH=r\tan 60{}^\circ =\frac{5\sqrt{3}}{6}$ Do đó $V=\frac{1}{3}SH.{{S}_{ABC}}=\frac{5\sqrt{3}}{3}$. Chọn A. |
Bài tập 5: Cho hình chóp S.ABC có đáy là tam giác ABC cân tại A có AB = AC= 10, BC= 12. Các mặt bên của khối chóp đều tạo với đáy một góc bằng nhau và bằng ${{30}^{o}}$. Thể tích khối chóp đã cho là
|
Lời giải chi tiết:
| Do các mặt bên của khối chóp đều tạo với đáy một góc bằng nhau nên hình chiếu vuông góc của đỉnh S xuống mặt đáy trùng với tâm đường tròn nội tiếp tam giác ABC.
Gọi M là trung điểm của BC$\Rightarrow $AM $\bot $BC Ta có:$AM=\sqrt{A{{B}^{2}}-B{{M}^{2}}}=\sqrt{{{10}^{2}}-{{6}^{2}}}=8$. Khi đó: ${{S}_{ABC}}=\frac{1}{2}AM.BC=48\Rightarrow {{r}_{ABC}}=\frac{S}{p}=\frac{48}{\frac{10+10+12}{2}}=3$$\Rightarrow SH=r\tan 30{}^\circ =\sqrt{3}$$\Rightarrow $$V=\frac{1}{3}SH.{{S}_{ABC}}=16\sqrt{3}$.Chọn C.
|
..
