Cách giải Tính Thể tích khối chóp đều – Bài tập đáp án chi tiết
Khối chóp đều là gì?
Khối chóp đều là khối chóp có đáy là đa giác đều và các cạnh bên bằng nhau.
Khối chóp tam giác đều
Khối chóp tam giác đều là khối chóp có đáy là tam giác đều và các cạnh bên bằng nhau.
Nếu cho khối chóp đều S.ABC thì ta có:
– Tam giác ABC là tam giác đều và các cạnh bên SA=SB=SC.
– Hình chiếu vuông góc của đỉnh S xuống mặt đáy trùng với trọng tâm G (cũng là trực tâm, tâm đường tròn ngoại tiếp, nội tiếp) của tam giác đều ABC tức là SG $\bot $(ABC).
– Các cạnh bên bằng nhau và đều tạo với đáy một góc bằng nhau.
– Các mặt bên là tam giác cân bằng nhau và các mặt phẳng bên đều tạo với đáy các góc bằng nhau.
Tứ diện đều là tứ diện có tất cả các cạnh bằng nhau.
Như vậy khối tứ diện đều là một trường hợp đặc biệt của khối chóp tam giác đều.
Khối tứ diện đều là khối chóp tam giác đều có cạnh bên bằng cạnh đáy.
Khối chóp tứ giác đều
Khối chóp tứ giác đều là khối chóp có đáy là hình vuông và các cạnh bên bằng nhau.
Nếu cho khối chóp đều S.ABCD thì ta có:
– Tứ giác ABCD là hình vuông và các cạnh bên SA = SB = SC = SD.
– Hình chiếu vuông góc của đỉnh S xuống mặt đáy trùng với tâm O của hình vuông ABCD tức là SO$\bot $ (ABCD).
– Các cạnh bên bằng nhau và đều tạo với đáy một góc bằng nhau.
– Các mặt bên là các tam giác cân bằng nhau và các mặt phẳng bên đều tạo với đáy các góc bằng nhau.
Bài tập trắc nghiệm thể tích khối chóp đều có đáp án chi tiết
Bài tập 1: Cho khối chóp tứ giác đều có cạnh đáy bằng $a$, cạnh bên gấp hai lần cạnh đáy. Tính thể tích V của khối chóp đã cho.
|
Lời giải chi tiết:
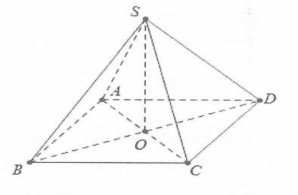
Giả sử khối chóp S.ABCD đều có đáy là hình vuông cạnh $a$tâm O và cạnh bên SD=$2a$. Khi đó SO $\bot $ (ABCD).
Ta có: $2O{{D}^{2}}={{a}^{2}}\Rightarrow OD=\frac{{{a}^{2}}}{2};SO=\sqrt{{{\left( 2a \right)}^{2}}-\frac{{{a}^{2}}}{2}}=a\sqrt{\frac{7}{2}}$
${{S}_{ABCD}}={{a}^{2}}$; ${{V}_{S.ABCD}}=\frac{1}{3}SO.{{S}_{ABCD}}=\frac{1}{3}{{a}^{2}}.\sqrt{\frac{7}{2}}a=\frac{{{a}^{3}}\sqrt{14}}{6}$. Chọn A
| Bài tập 2: Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng $a$, cạnh bên bằng $2a$. Tính thể tích V của khối chóp S.ABC
A. V= $\frac{\sqrt{13}{{a}^{3}}}{12}$. B. V= $\frac{\sqrt{11}{{a}^{3}}}{12}$. C. V=$\frac{\sqrt{11}{{a}^{3}}}{6}$. D. V=$\frac{\sqrt{11}{{a}^{3}}}{4}$. |
Lời giải chi tiết:
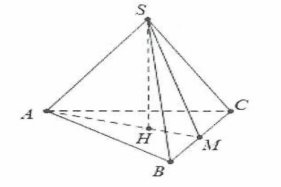
| Gọi H là trọng tâm của $\Delta $ABC và M là trung điểm của BC.
Ta có AM=$\frac{a\sqrt{3}}{2}$$\Rightarrow $AH=$\frac{2}{3}$AM=$\frac{a\sqrt{3}}{3}$; ${{S}_{ABC}}=\frac{{{a}^{2}}\sqrt{3}}{4}$. Mặt khác: $SH=\sqrt{S{{A}^{2}}-A{{H}^{2}}}=\sqrt{4{{a}^{2}}-{{\left( \frac{a\sqrt{3}}{3} \right)}^{2}}}=\frac{a\sqrt{33}}{3}$. Do đó ${{V}_{S.ABC}}=\frac{1}{3}SH.{{S}_{ABC}}=\frac{{{a}^{3}}\sqrt{11}}{12}$. Chọn B. |
| Bài tập 3: Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh $a$, cạnh bên tạo với đáy một góc bằng $60{}^\circ $. Tính thể tích khối chóp đã cho.
A.$\frac{{{a}^{3}}\sqrt{3}}{4}$ . B. $\frac{{{a}^{3}}\sqrt{3}}{8}$ . C. $\frac{{{a}^{3}}\sqrt{3}}{12}$. D. $\frac{{{a}^{3}}\sqrt{3}}{24}$. |
Lời giải chi tiết:
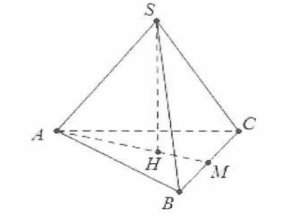
Gọi H là trọng tâm tam giác ABC suy ra $SH\bot \left( ABC \right)$.
Gọi M là trung điểm của BC ta có $AM=\frac{a\sqrt{3}}{2}$.
Khi đó $AH=\frac{2}{3}AM\Rightarrow \frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}$.
Lại có $\widehat{SAH}={{60}^{o}}\Rightarrow SH=HA\tan {{60}^{o}}=a$
Suy ra: ${{V}_{S.ABC}}=\frac{1}{3}SH.{{S}_{ABC}}=\frac{1}{3}a.\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{{{a}^{3}}\sqrt{3}}{12}$ Chọn C.
| Bài tập 4: Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh $a$, cạnh bên tạo với đáy một góc bằng $60{}^\circ $. Tính thể tích khối chóp đã cho.
A.$\frac{{{a}^{3}}\sqrt{3}}{4}$ . B. $\frac{{{a}^{3}}\sqrt{3}}{8}$ . C. $\frac{{{a}^{3}}\sqrt{3}}{12}$. D. $\frac{{{a}^{3}}\sqrt{3}}{24}$. |
Lời giải chi tiết:

| Gọi H là trọng tâm tam giác ABC suy ra $SH\bot \left( ABC \right)$.
Gọi M là trung điểm của BC ta có $AM=\frac{a\sqrt{3}}{2}$. Khi đó $HM=\frac{1}{3}AM\Rightarrow \frac{1}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{6}$. Lại có $\left\{ \begin{align} & BC\bot SA \\ & BC\bot AM \\ \end{align} \right.\Rightarrow BC\bot \left( SAM \right)$ Do đó $\widehat{SMH}=\widehat{\left( \left( SBC \right);\left( ABC \right) \right)}=60{}^\circ \Rightarrow SH=HM\tan 60{}^\circ =\frac{a}{2}$ Do đó ${{V}_{S.ABC}}=\frac{1}{3}SH.{{S}_{ABC}}=\frac{1}{3}.\frac{a}{2}.\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{{{a}^{3}}\sqrt{3}}{24}$. Chọn D. |
| Bài tập 5: Cho hình chóp đều S.ABCD có đáy là hình vuông cạnh $a$, mặt bên tạo với đáy một góc bằng $30{}^\circ $. Tính thể tích V của khối chóp S.ABCD theo $a$ và $30{}^\circ $.
A.V=$\frac{{{a}^{3}}\sqrt{3}}{6}$ . B. V= $\frac{{{a}^{3}}\sqrt{3}}{9}$ . C.V= $\frac{{{a}^{3}}\sqrt{3}}{12}$. D. V=$\frac{{{a}^{3}}\sqrt{3}}{18}$. |
Lời giải chi tiết:
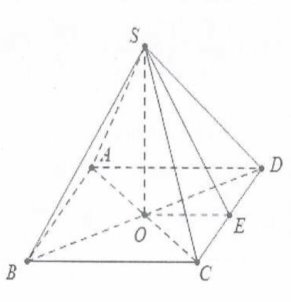
| Gọi O là tâm của hình vuông ABCD khi đó $SO\bot \left( ABCD \right)$và ${{S}_{ABCD}}={{a}^{2}}$.
Dựng $OE\bot CD$, lại có $CD\bot \text{SO}$$\Rightarrow \text{CD}\bot \left( SEO \right)$. Khi đó ta có: $\widehat{\left( \left( SCD \right),\left( ABCD \right) \right)}=\widehat{SEO}=30{}^\circ $. Mặt khác $OE=\frac{BC}{2}$(đường trung bình trong tam giác) nên $OE=\frac{a}{2}\Rightarrow SO=OE\tan 30=\frac{a\tan 30{}^\circ }{2}=\frac{a}{2\sqrt{3}}$. Khi đó ${{V}_{S.ABCD}}=\frac{1}{3}SO.{{S}_{ABCD}}=\frac{{{a}^{3}}}{6\sqrt{3}}=\frac{{{a}^{3}}\sqrt{3}}{18}$. Chọn D. |
| Bài tập 6: Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2a. Thể tích khối chóp đã cho bằng:
A. $\frac{4{{a}^{3}}\sqrt{2}}{3}$ . B. $\frac{8{{a}^{3}}}{3}$ . C. $\frac{8{{a}^{3}}\sqrt{2}}{3}$. D. $\frac{2{{a}^{3}}\sqrt{2}}{3}$. |
Lời giải chi tiết:
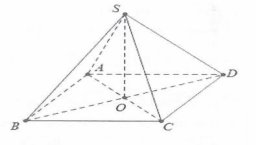
| Gọi O = $AC\cap BD$ , ta có $SO\bot (ABCD)$ và đáy ABCD là hình vuông.
Ta có: ${{S}_{ABCD}}=4{{a}^{2}}$, $OB=\frac{BC}{\sqrt{2}}=a\sqrt{2}$. $\Rightarrow SO=\sqrt{S{{B}^{2}}-O{{B}^{2}}}=a\sqrt{2}$. $\Rightarrow $ ${{V}_{S.ABCD}}=\frac{1}{3}SO.{{S}_{ABCD}}=\frac{1}{3}.a\sqrt{2}.A{{B}^{2}}=\frac{4{{a}^{3}}\sqrt{2}}{3}$ Chọn |
| Bài tập 7: Cho hình chóp đều S.ABCD có đáy là hình vuông cạnh 4a. Khoảng cách từ điểm D đến mặt phẳng (SAB) bằng $\frac{4a}{\sqrt{5}}$. Thể tích khối chóp đã cho là:
A. $\frac{{{a}^{3}}}{3}$ . B. $\frac{2{{a}^{3}}}{3}$ . C. $\frac{16{{a}^{3}}}{3}$. D. $\frac{4{{a}^{3}}}{3}$. |
Lời giải chi tiết:
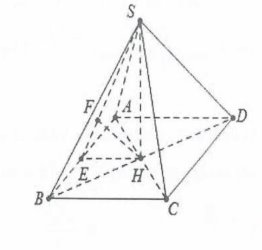
Gọi H là tâm của hình vuông suy ra $SH\bot (ABCD)$
Khi đó ta có:$d\left( D;\left( SAB \right) \right)=2d\left( H;\left( SAB \right) \right)$
Dựng $HE\bot AB$ và $HF\bot SE$ ta chứng minh được
$d\left( H;\left( SAB \right) \right)=HF\Rightarrow d\left( D;\left( SAB \right) \right)=2HF=\frac{4a}{\sqrt{5}}$
Do vậy $HF=\frac{2a}{\sqrt{5}}$. Lại có $HE=2a$
Ta có:$\frac{1}{H{{E}^{2}}}+\frac{1}{S{{H}^{2}}}=\frac{1}{H{{F}^{2}}}\Rightarrow SH=a$
Vậy ${{V}_{S.ABCD}}=\frac{1}{3}SH.{{S}_{ABCD}}=\frac{16{{a}^{3}}}{3}$ . Chọn C.
| Bài tập 8: Cho hình chóp đều S.ABCD có mặt bên tạo với đáy một góc $60{}^\circ $. Cạnh bên SA=$a\sqrt{5}$. Thể tích khối chóp S.ABCD là:
A. $\frac{{{a}^{3}}\sqrt{6}}{3}$ . B. $\frac{{{a}^{3}}\sqrt{3}}{3}$ . C. $\frac{2{{a}^{3}}\sqrt{2}}{3}$. D. $\frac{4{{a}^{3}}\sqrt{3}}{3}$. |
Lời giải chi tiết:
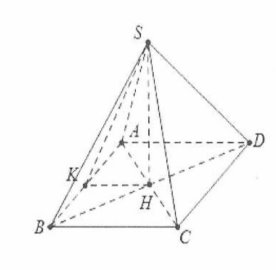
Gọi H là tâm của hình vuông suy ra$SH\bot \left( ABCD \right)$.
Đặt $AB=2x$. Dựng $HK\bot AB$
Ta có: $SH\bot AB\Rightarrow HK\bot \left( SAB \right)$
Do vậy $\widehat{\left( \left( SAB \right);\left( ABCD \right) \right)}=\widehat{SKH}=60{}^\circ $
Lại có $HK=x\Rightarrow SH=x\tan 60{}^\circ =x\sqrt{3}$.
Khi đó $S{{A}^{2}}=S{{H}^{2}}+H{{A}^{2}}=3{{x}^{2}}+2{{x}^{2}}=5{{x}^{2}}$
$\Rightarrow x=a\Rightarrow SH=a\sqrt{3}$, ${{S}_{ABCD}}=A{{B}^{2}}=4{{a}^{2}}$.
$\Rightarrow $ ${{V}_{S.ABCD}}=\frac{1}{3}SH.{{S}_{ABCD}}=\frac{4{{a}^{3}}\sqrt{3}}{3}$. Chọn D.
| Bài tập 9: Cho khối chóp đều S.ABCD có đáy là hình vuông cạnh $2a$, biết diện tích của tam giác SCD là $3{{a}^{2}}$. Thể tích khối chóp S.ABCD là:
A. $\frac{{{a}^{3}}\sqrt{3}}{8}$ . B. $\frac{8{{a}^{3}}\sqrt{2}}{3}$ . C. $\frac{3{{a}^{3}}\sqrt{3}}{4}$. D. $\frac{4{{a}^{3}}\sqrt{2}}{3}$. |
Lời giải chi tiết:
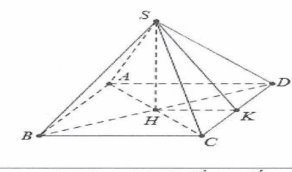
Gọi H là tâm của hình vuông suy ra $SH\bot (ABCD)$.
Gọi K là trung điểm của CD. Khi đó ta có $SK\bot CD$.
Lại có: ${{S}_{ACD}}=\frac{1}{2}CD.SK=a.SK=3{{a}^{2}}$
$\Rightarrow SK=3a\Rightarrow SH=\sqrt{S{{K}^{2}}-H{{K}^{2}}}=2a\sqrt{2}$, ${{S}_{ABCD}}=4{{a}^{2}}$
Vậy ${{V}_{S.ABCD}}=\frac{1}{3}SH.{{S}_{ABCD}}=\frac{8{{a}^{3}}\sqrt{2}}{3}$. Chọn B.
| Bài tập 10: Cho hình chóp S.ABC có đáy là tam giác đều cạnh $a$ . Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng $\frac{3a}{4}$. Thể tích khối chóp đã cho là:
A. $\frac{{{a}^{3}}\sqrt{3}}{6}$ . B. $\frac{{{a}^{3}}\sqrt{3}}{8}$ . C. $\frac{{{a}^{3}}\sqrt{3}}{12}$. D. $\frac{{{a}^{3}}\sqrt{3}}{24}$. |
Lời giải chi tiết:
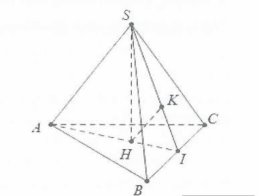
Gọi H là trọng tâm tam giác đều ABC ta có:$SH\bot (ABC)$.
Khi đó $d\left( A;\left( SBC \right) \right)=3d\left( H;\left( SBC \right) \right)=\frac{3a}{4}$
Suy ra $d\left( H;\left( SBC \right) \right)=\frac{a}{4}$. Gọi I là trung điểm của BC dễ thấy $AI\bot BC$ .
Dựng $HK\bot SI$
Ta có: $\left\{ \begin{align} & BC\bot SH \\ & BC\bot AI \\ \end{align} \right.\Rightarrow BC\bot HK\Rightarrow HK\bot \left( SBC \right)$.
Do vậy $d\left( H;\left( SBC \right) \right)=HK=\frac{a}{4}$; $HI=\frac{a\sqrt{3}}{6}$
Mặt khác $\frac{1}{H{{K}^{2}}}=\frac{1}{S{{H}^{2}}}+\frac{1}{H{{I}^{2}}}\Rightarrow SH=\frac{a}{2}$.
Vậy ${{V}_{S.ABC}}=\frac{1}{3}SH.{{S}_{ABC}}=\frac{1}{3}.\frac{a}{2}.\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{{{a}^{3}}\sqrt{3}}{24}$. Chọn D.
| Bài tập 11: Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a. Biết tam giác ASB vuông, thể tích khối chóp S.ABC là:
A. $\frac{{{a}^{3}}\sqrt{2}}{24}$ . B. $\frac{{{a}^{3}}\sqrt{2}}{32}$ . C. $\frac{{{a}^{3}}\sqrt{2}}{16}$. D. $\frac{{{a}^{3}}\sqrt{2}}{8}$. |
Lời giải chi tiết:
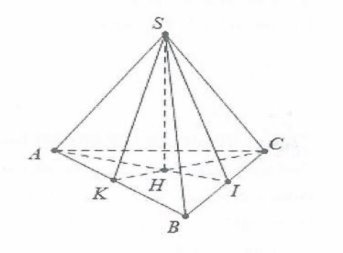
Gọi H là trọng tâm của tam giác ABC
Khi đó $SH\bot (ABC)$ . Do $SA=SB$ nên tam giác SAB vuông khi và chỉ khi tam giác ASB vuông tại S
Khi đó gọi K là trung điểm của AB ta có:
$SK=\frac{AB}{2}=\frac{a}{2}$. Mặt khác $CK=\frac{a\sqrt{3}}{2}\Rightarrow HK=\frac{a\sqrt{3}}{6}$
Suy ra $SH=\sqrt{S{{K}^{2}}-H{{K}^{2}}}=\frac{a}{\sqrt{6}}$.
Do đó ${{V}_{S.ABC}}=\frac{1}{3}SH.{{S}_{ABC}}=\frac{{{a}^{3}}\sqrt{2}}{24}$. Chọn A.
