Bài tập Sử dụng định lý hình chiếu để tính góc giữa hai mặt phẳng
Dưới đây là một số bài tập góc giữa hai mặt phẳng có đáp án chi tiết
| Bài tập 1: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, $SA\bot \left( ABC \right)$. Trên cạnh SA lấy điểm M sao cho diện tích tam giác MBC bằng $\frac{{{a}^{2}}\sqrt{3}}{2}$. Tính góc giữa hai mặt phẳng (MBC) và (ABC). |
Lời giải chi tiết
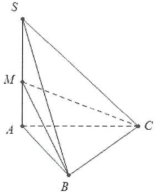
Ta có: ${{S}_{ABC}}=\frac{{{a}^{2}}\sqrt{3}}{4}$. Gọi $\varphi =\widehat{\left( \left( MBC \right);\left( ABC \right) \right)}$
Do $\Delta ABC$ là hình chiếu của tam giác MBC trên mặt phẳng (ABC) do đó $\cos \varphi =\frac{{{S}_{ABC}}}{{{S}_{MBC}}}=\frac{\frac{{{a}^{2}}\sqrt{3}}{4}}{\frac{{{a}^{2}}\sqrt{3}}{2}}=\frac{1}{2}\Rightarrow \varphi =60{}^\circ .$
| Bài tập 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, $SA\bot \left( ABCD \right)$. Gọi N là trung điểm của SA, mặt phẳng (NCD) cắt khối chóp theo một thiết diện có diện tích $S=2{{a}^{2}}\sqrt{3}$. Tính góc giữa mặt phẳng (NDC) và mặt phẳng (ABCD). |
Lời giải chi tiết
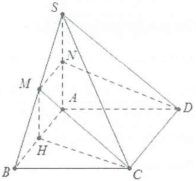
Đặt $\varphi =\widehat{\left( \left( NCD \right);\left( ABCD \right) \right)}.$
Do $CD//AB\Rightarrow \left( NCD \right)$ cắt (SAB) theo thiết diện $NM//AB\Rightarrow $ MN là đường trung bình của tam giác SAB.
Khi đó thiết diện là tứ giác MNDC.
Gọi H là hình chiếu của M trên mặt phẳng (ABCD) thì
H là trung điểm của AB và ${{S}_{ABCD}}=\frac{a+2a}{2}.2a=3{{a}^{2}}.$
Do tứ giác HADC là hình chiếu của tứ giác MNDC trên
mặt phẳng (ABCD) $\Rightarrow \cos \varphi =\frac{{{S}_{AHCD}}}{{{S}_{NMCD}}}=\frac{3{{a}^{2}}}{2{{a}^{2}}\sqrt{3}}=\frac{\sqrt{3}}{2}.$
Do đó $\varphi =30{}^\circ .$
| Bài tập 4: Cho hình lăng trụ đứng $ABC.{A}'{B}'{C}’$ có đáy ABC là tam giác cân với $AB=AC=a$, $\widehat{BAC}=120{}^\circ $, cạnh bên $B{B}’=a$, gọi I là trung điểm của $C{C}’$. Chứng minh rằng tam giác $A{B}’I$ vuông tại A và tính cosin góc giữa hai mặt phẳng $\left( A{B}’I \right)$ và (ABC). |
Lời giải chi tiết
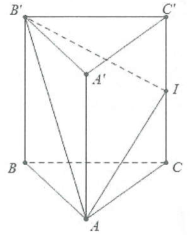
Ta có: $BC={B}'{C}’=\sqrt{A{{B}^{2}}+A{{C}^{2}}-2AB.AC\cos \widehat{BAC}}=a\sqrt{3}.$
Mặt khác $\left\{ \begin{array} {} A{B}’=\sqrt{A{{B}^{2}}+B{{{{B}’}}^{2}}}=a\sqrt{2} \\ {} AI=\sqrt{A{{C}^{2}}+C{{I}^{2}}}=\frac{a\sqrt{5}}{2} \\ {} {B}’I=\sqrt{{B}'{{{{C}’}}^{2}}+{C}'{{I}^{2}}}=\frac{a\sqrt{13}}{2} \\ \end{array} \right..$
Do $A{{{B}’}^{2}}+A{{I}^{2}}={B}’I=\frac{13{{a}^{2}}}{4}\Rightarrow \Delta {B}’AI$ vuông tại A.
Ta có: ${{S}_{A{B}’I}}=\frac{1}{2}A{B}’.AI=\frac{{{a}^{2}}\sqrt{10}}{4}.$
${{S}_{ABC}}=\frac{1}{2}AB.ACsin\widehat{BAC}=\frac{{{a}^{2}}\sqrt{3}}{4}\Rightarrow \cos \widehat{\left( \left( A{B}’I \right);\left( ABC \right) \right)}=\frac{{{S}_{ABC}}}{{{S}_{A{B}’I}}}=\frac{\sqrt{30}}{10}.$
| Bài tập 5: Cho hình lăng trụ đứng $ABCD.{A}'{B}'{C}'{D}’$ có đáy là hình vuông cạnh a và chiều cao $A{A}’=6a$. Trên $C{C}’$ lấy điểm M, trên $D{D}’$ lấy điểm N sao cho $CM=2MC$ và $DN=2N{D}’$. Tính cosin góc giữa 2 mặt phẳng $\left( {B}’MN \right)$ và (ABCD). |
Lời giải chi tiết
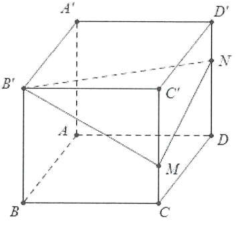
Gọi $\varphi =\widehat{\left( \left( {B}’MN \right);\left( ABCD \right) \right)}.$
Ta có: ${{S}_{BCD}}=\frac{{{a}^{2}}}{2};{D}’N=2a;{C}’M=4a$
Lại có: ${B}'{D}’=a\sqrt{2}\Rightarrow {B}’N=\sqrt{{B}'{{{{D}’}}^{2}}+{D}'{{N}^{2}}}=a\sqrt{6}$
${B}’M=\sqrt{{B}'{{{{C}’}}^{2}}+{C}'{{M}^{2}}}=a\sqrt{17},$
$MN=\sqrt{{{a}^{2}}+{{\left( 2a \right)}^{2}}}=a\sqrt{5}.$
Theo công thức Herong $S=\sqrt{p\left( p-a \right)\left( p-b \right)\left( p-c \right)}$
Ta tính được: ${{S}_{BMN}}=\frac{\sqrt{21}}{2}.$
Do $\Delta BCD$ là hình chiếu của $\Delta {B}’MN$ trên mặt phẳng (ABCD) nên $\cos \varphi =\frac{{{S}_{BCD}}}{{{S}_{{B}’MN}}}=\frac{1}{\sqrt{21}}.$
