Cách tìm nhanh giao điểm của đường thẳng với mặt phẳng – bài tập có đáp án
Đường thẳng a cắt mp (P) tại một điểm M. Điểm M đó gọi là giao điểm của đường thẳng a và mp (P). Kí hiệu: $a\cap \left( P \right)=M.$
Phương pháp giải xác định giao điểm của đường thẳng và mặt phẳng
Ta đi tìm một đường thẳng b nào đó nằm trong mặt phẳng (P) mà b cắt đường thẳng a tại một điểm M. Khi đó: $a\cap \left( P \right)=M.$
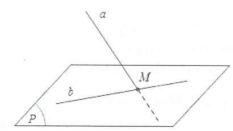
Trong trường hợp đường thẳng b chưa có sẵn ta có thể dựa vào phương pháp sau để tìm giao điểm
– Bước 1: Dựa vào hình vẽ xác định một mặt phẳng chứa đường thẳng a.
Giả sử xác định được mp (Q) chứa a.
– Bước 2: Xác định giao tuyến của mp (P) và mp (Q).
Giả sử $\left( P \right)\cap \left( Q \right)=b$ .
– Bước 3: Xác định giao điểm của đường thẳng a và giao tuyến b. Do a và b cùng nằm trong mp (Q) nên $a\cap b=M.$
Kết luận: $M\in a;M\in \left( P \right).$ Vậy $M=a\cap \left( P \right).$
Bài tập trắc nghiệm tìm giao điểm của đường thẳng và mặt phẳng trong không gian có đáp án chi tiết
| Bài tập 1: Cho hình chóp S.ABCD. Trong tam giác SBC lấy một điểm M, trong tam giác SCD lấy một điểm N.
a) Tìm giao tuyến của mặt phẳng (SMN) và (ABCD). b) Tìm giao điểm của MN và (SAC). c) Tìm giao điểm của SC với (AMN). |
Lời giải chi tiết
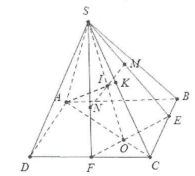
a) Trong mặt phẳng (SBC) gọi $E=SM\cap BC\Rightarrow E=\left( SMN \right)\cap \left( ABCD \right).$
Trong mặt phẳng (SCD) gọi $F=SN\cap CD\Rightarrow F=\left( SMN \right)\cap \left( ABCD \right).$
Do đó $\text{EF}=\left( SMN \right)\cap \left( ABCD \right).$
b) Ta có: $SO=\left( SMN \right)\cap \left( SAC \right).$
Trong mặt phẳng (SEF) gọi $I=MN\cap SO.$
Do đó $I=MN\cap \left( SAC \right).$
c) Dễ thấy $AI=\left( AMN \right)\cap \left( SAC \right).$
Trong mặt phẳng (SAC) gọi $K=AI\cap SC\Rightarrow K=SC\cap \left( AMN \right)$ .
| Bài tập 2: Cho tứ diện ABCD, gọi M, N là hai điểm lần lượt trên AC và AD. Điểm O là một điểm bên trong DBCD. Tìm giao điểm của:
a) MN và (ABO). b) AO và (BMN). |
Lời giải chi tiết
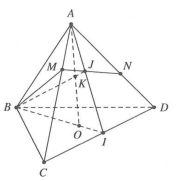
a) Trong mặt phẳng (BCD) kẻ BO giao CD tại I. Trong (ACD) kẻ MN giao AI tại J $\Rightarrow $ J là giao điểm của MN và (ABO).
b) Trong mặt phẳng (ABI): AO giao BJ tại K $\Rightarrow $ K là giao điểm của AO và (BMN).
| Bài tập 3: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC. K là một điểm trên cạnh BD và không trùng với trung điểm của BD. Tìm giao điểm của CD và AD với mặt phẳng (MNK). |
Lời giải chi tiết
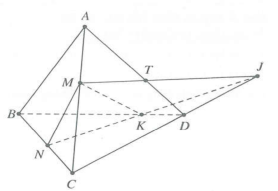
Trong mặt phẳng (BCD): NK giao CD tại điểm J $\Rightarrow $ J là giao điểm của CD với mp (MNK). Trong mặt phẳng (ACD): MJ giao với AD tại điểm T$\Rightarrow $ T là giao điểm của AD với mp(MNK).
| Bài tập 4: Cho hình chóp S.ABCD. Điểm M là một điểm trên cạnh SC.
a) Tìm giao điểm của AM và (SBD). b) Gọi N là một điểm trên cạnh BC. Tìm giao điểm của SD và (AMN). |
Lời giải chi tiết
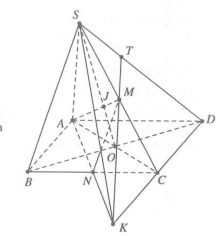
a) Trong mp(ABCD): AC giao BD tại O. Trong mp(SAC) thì SO giao MA tại J.
Từ đó thì J chính là giao điểm của AM và (SBD).
b) Giả sử AN giao CD tại K
Trong mp(SCD): KM giao SD tại T, từ đó T chính là giao điểm của SD và (AMN).
Nếu AN và CD song song với nhau, ta chỉ việc kẻ MT song song với CD (T thuộc SD) từ đó cũng suy ra được T là điểm cần tìm.
| Bài tập 5: Cho hình chóp S.ABCD, gọi O là giao điểm của AC và BD, điểm M thuộc cạnh SC và điểm K là giao điểm của AM và SO. Có bao nhiêu khẳng định đúng trong các khẳng định sau:
(1).$\left( SAC \right)\cap \left( SBD \right)=SO$ (2).$\left( ABM \right)\cap SD=N$ với N là giao điểm của BK và SD. (3). $\left( ABM \right)\cap \left( SCD \right)=MD.$ (4). $\left( ABM \right)\cap \left( SAD \right)=AN$ với N là giao điểm của BK và SD. A. 1 B.2 C.3 D.4 |
Lời giải chi tiết
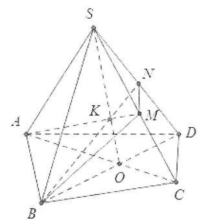
Gọi N là giao điểm của BK và SD.
Ta có: $\left( SAC \right)\cap \left( SBD \right)=SO$
$\left( ABM \right)\cap SD=N;$ $\left( ABM \right)\cap (SCD)=MN$
Và $\left( ANM \right)\cap \left( SAD \right)=AN$
Các khẳng định đúng là 1, 2 và 4. Khẳng định 3 sai. Chọn C.
| Bài tập 6: Cho hình chóp S.ABCD, gọi O là giao điểm của AC và BD, I là giao điểm của AB và CD, J là giao điểm của AD và BC. Có bao nhiêu khẳng định đúng trong các khẳng định sau:
(1). $\left( SAC \right)\cap \left( SBD \right)=SO.$ (2). Mặt phẳng (SBD) cắt IJ tại giao điểm của BD và IJ. (3). $\left( SAD \right)\cap \left( SBC \right)=SI$ (4). $\left( SAB \right)\cap \left( SCD \right)=SJ.$ A. 1. B. 2. C. 3. D. 4. |
Lời giải chi tiết
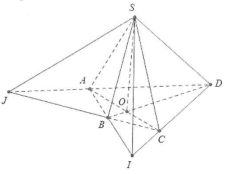
Ta có: $\left( SAC \right)\cap \left( SBD \right)=SO$
$\left( SAD \right)\cap \left( SBC \right)=SJ$ và $\left( SAB \right)\cap \left( SCD \right)=SI.$
Các khẳng định đúng là 1 và 2.
Khẳng định sai là 3 và 4. Chọn B.
