Tổng hợp lý thuyết phương pháp giản đồ véc tơ là gì? lý thuyết tóm tắt ngắn gọn vật lý lớp 12

LÝ THUYẾT TRỌNG TÂM, PHƯƠNG PHÁP GIẢI VÀ BÀI TẬP GIẢN ĐỒ VECTƠ

Dạng 1. Phương pháo vecto buộc (vecto chung gốc)

Lý thuyết chung và phương pháp giải:

TH1: Mạch RLC có $\overrightarrow{{{U}_{RL}}}\bot \overrightarrow{{{U}_{RC}}}$:

Đặc điểm: ${{\varphi }_{1}}-{{\varphi }_{2}}=\frac{\pi }{2}\Rightarrow \tan {{\varphi }_{1}}\tan {{\varphi }_{2}}=-1.$

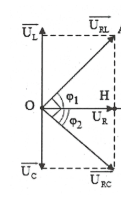Áp dụng hệ thức lượng trong tam giác vuông ta có:

$+)\text{ }O{{H}^{2}}=HA.HB\Rightarrow U_{R}^{2}={{U}_{L}}{{U}_{C}}\Rightarrow {{R}^{2}}={{Z}_{L}}{{Z}_{C}}=\frac{L}{C}.$

$+)\text{ }\frac{1}{U_{R}^{2}}=\frac{1}{U_{RL}^{2}}+\frac{1}{U_{RC}^{2}}.$

$\begin{array}{} +)\text{ }O{{A}^{2}}=AB.AH\Rightarrow U_{RL}^{2}=({{U}_{L}}+{{U}_{C}}).{{U}_{L}} \\ {} U_{RC}^{2}=({{U}_{L}}+{{U}_{C}}).{{U}_{C}}. \\ \end{array}$

$+)\text{ }OH.AB=OA.OB\Rightarrow {{U}_{R}}.({{U}_{L}}+{{U}_{C}})={{U}_{RL}}.{{U}_{RC}}.$

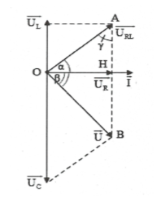
TH2: Mạch RLC có $\overrightarrow{{{U}_{RL}}}\bot \overrightarrow{U}$

Ta có: $\overrightarrow{U}\bot \overrightarrow{{{U}_{RL}}}$nên trong tam giác OAB vuông tại O

có đường cao OH ta có:

+) Định lý Pytago: ${{U}^{2}}+U_{RL}^{2}=U_{C}^{2}.$

$+)\frac{1}{{{h}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}\Rightarrow \frac{1}{U_{R}^{2}}=\frac{1}{{{U}^{2}}}+\frac{1}{U_{RL}^{2}}.$

$\begin{array}{} +)\text{ }O{{B}^{2}}=AB.HB\Rightarrow {{U}^{2}}={{U}_{C}}.({{U}_{C}}-{{U}_{L}}). \\ {} O{{A}^{2}}=HA.AB\Rightarrow U_{RL}^{2}={{U}_{L}}.{{U}_{C}}\Leftrightarrow U_{R}^{2}+U_{L}^{2}={{U}_{L}}.{{U}_{C}} \\ {} \Rightarrow {{R}^{2}}+Z_{L}^{2}={{Z}_{L}}.{{Z}_{C}}. \\ \end{array}$

$\begin{array}{} +)\text{ }OH.AB=OA.OB={{U}_{R}}.{{U}_{C}}={{U}_{RL}}.U=2{{S}_{OAB}}. \\ {} \Rightarrow {{Z}_{L}}.{{Z}_{C}}={{R}^{2}}+Z_{L}^{2}. \\ {} +)\text{ tan}{{\varphi }_{RL}}.\tan \varphi =-1. \\ \end{array}$

TH3: Mạch RLC có $\overrightarrow{{{U}_{RC}}}\bot \overrightarrow{U}$.

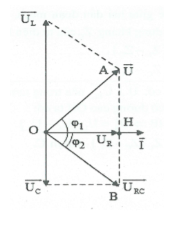Ta có: $\overrightarrow{U}\bot \overrightarrow{{{U}_{RC}}}$nên trong tam giác OAB vuông tại O

có đường cao OH ta có:

$\begin{array}{} +)\text{ }O{{B}^{2}}=AB.HB\Rightarrow {{U}_{L}}.{{U}_{C}}=U_{R}^{2}+U_{C}^{2} \\ {} \Rightarrow {{Z}_{L}}.{{Z}_{C}}={{R}^{2}}+Z_{C}^{2}. \\ \end{array}$

+) Định lý Pytago: ${{U}^{2}}+U_{RC}^{2}=U_{L}^{2}.$

$+)\frac{1}{{{h}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}\Rightarrow \frac{1}{U_{R}^{2}}=\frac{1}{{{U}^{2}}}+\frac{1}{U_{RC}^{2}}.$

$+)\text{ }O{{A}^{2}}=AB.HA\Rightarrow {{U}^{2}}={{U}_{L}}.({{U}_{L}}-{{U}_{C}}).$

$+)\text{ }OH.AB=OA.OB={{U}_{R}}.{{U}_{L}}={{U}_{RC}}.U=2{{S}_{OAB}}.$

$+)\text{ }\tan \varphi .\tan {{\varphi }_{RC}}=-1.$

VÍ DỤ MINH HỌA DẠNG 1.

Bài tập 1: Cho mạch điện LRC nối tiếp theo thứ tự trên. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có biểu thức $u={{U}_{0}}c\text{os}(100\pi t)V$thì ${{U}_{RL}}=160V$;${{U}_{C}}=72V.$Biết cường độ dòng điện trong mạch $I=2A$ và điện áp ${{u}_{RL}}$ lệch pha $\pi /2$ so với ${{u}_{RC}}$ tính R, ${{Z}_{L}}$,${{Z}_{C}}$ và ${{U}_{0}}$.

HD giải: Vẽ giản đồ vecto như hình vẽ.

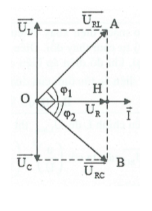Ta có: $O{{A}^{2}}=HA.AB\Rightarrow {{160}^{2}}=AB.(AB-72)$

$\Rightarrow AB=200\Rightarrow {{U}_{L}}=HA=128V.$

Mặt khác: $O{{H}^{2}}=HA.HB\Rightarrow {{U}_{R}}=\sqrt{{{U}_{L}}{{U}_{C}}}=96V.$

Suy ra $R=48\Omega ,{{Z}_{L}}=64\Omega $ và ${{Z}_{C}}=36\Omega .$

Lại có: $U=\sqrt{U_{R}^{2}+{{({{U}_{L}}-{{U}_{C}})}^{2}}}=8\sqrt{193}$

$\Rightarrow {{U}_{0}}=U\sqrt{2}=8\sqrt{386}V.$

Bài tập 2: Đặt điện áp $u=200\cos 100\pi t(V)$ vào hai đầu đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn AM gồm cuộn cảm thuần L mắc nối tiếp với điện trở thuần R, đoạn MB chỉ có tụ điện C. Biết điệp áp giữa hai đầu đoạn mạch AM và điện áp giữa hai đầu đoạn mạch MB có giá trị hiệu dụng bằng nhau nhưng lệch pha nhau $2\pi /3.$Tính điện áp hiệu dụng giữa hai đầu đoạn mạch AM, giữa hai đầu điện trở R.

HD giải: Ta có: $\Delta AO{{U}_{C}}$ cân tại O có $\widehat{AO{{U}_{C}}}={{120}^{0}}.$

Mặt khác $OAB{{U}_{C}}$là hình bình hành có $OA=O{{U}_{C}}$nên

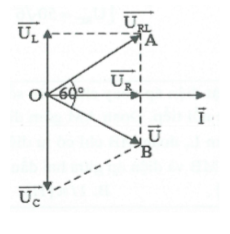$OAB{{U}_{C}}$ là hình thoi. Khi đó tam giác OAB và $OB{{U}_{C}}$

là các tam giác đều.

Do đó ${{U}_{AM}}={{U}_{AB}}={{U}_{MB}}=100\sqrt{2}V.$

${{U}_{R}}=\frac{OA\sqrt{3}}{2}=\frac{100\sqrt{6}}{2}=50\sqrt{5}V.$

Bài tập 3: [Trích đề thi đại học năm 2008] Cho đoạn mạch điện xoay chiều gồm cuộn dây có điện trở thuần R, mắc nối tiếp với tụ điện. Biết hiệu điện thế giữa hai đầu cuộn dây lệch pha $\pi /2$ so với hiệu điện thế giữa hai đầu đoạn mạch. Mối quan hệ giữa điện trở thuần R với cảm kháng${{Z}_{L}}$ của cuộn dây và dung kháng${{Z}_{C}}$ của tụ điện là:

A. ${{R}^{2}}={{Z}_{C}}({{Z}_{L}}-{{Z}_{C}}).$ B. ${{R}^{2}}={{Z}_{C}}({{Z}_{C}}-{{Z}_{L}}).$

C. ${{R}^{2}}={{Z}_{L}}({{Z}_{C}}-{{Z}_{L}}).$ D. ${{R}^{2}}={{Z}_{L}}({{Z}_{L}}-{{Z}_{C}}).$

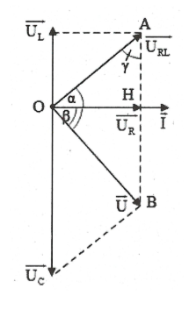HD giải: Ta có : $\overline{U}\bot \overline{{{U}_{RL}}}$nên trong tam giác OAB

vuông tại O có đường cao OH ta có:

$O{{H}^{2}}=HA.HB\Rightarrow U_{R}^{2}={{U}_{L}}.({{U}_{C}}-{{U}_{L}})$

Suy ra ${{R}^{2}}={{Z}_{L}}({{Z}_{C}}-{{Z}_{L}}).$Chọn C.

Bài tập 4: Cho mạch điện xoay chiều mắc nối tiếp theo thứ tự: điện trở R, tụ điện C và cuộn cảm thuần L có độ tự cảm thay đổi. Điều chỉnh độ tự cảm sao cho điện áp hiệu dụng trên cuộn cảm đạt giá trị cực đại, khi có điện áp hiệu dụng trên R là 100V và khi điện áp tức thời hai đầu đoạn mạch là $100\sqrt{5}V$ thì điện áp tức thời của đoạn mạch RC là $50\sqrt{2}V.$Điện áp hiệu dụng của đoạn mạch là:

A. 300V B. $100\sqrt{3}.$V C. $75\sqrt{2}.$ D. 200V.

HD giải: Điều chỉnh L để ${{U}_{Lm\text{ax}}}$ thì $\overline{{{U}_{RC}}}\bot \overline{U}.$

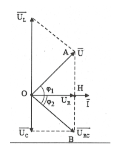Ta có: $\overline{U}\bot \overline{{{U}_{RC}}}$ nên ta có: ${{\left( \frac{u}{U} \right)}^{2}}+{{\left( \frac{{{u}_{RC}}}{{{U}_{RC}}} \right)}^{2}}=2.$

$\Leftrightarrow \frac{{{100}^{2}}.5}{{{U}^{2}}}+\frac{{{50}^{2}}.2}{U_{RC}^{2}}=2(1).$

Mặt khác $\frac{1}{U_{R}^{2}}=\frac{1}{{{U}^{2}}}+\frac{1}{U_{RC}^{2}}=\frac{1}{{{100}^{2}}}(2).$

Giải hệ(1) và (2) suy ra $\left\{ \begin{array}{} U=100\sqrt{3}V \\ {} {{U}_{RC}}=50\sqrt{6}V \\ \end{array} \right..$ Chọn B.

Bài tập 5: Đặt điện áp xoay chiều tần số 50Hz vào hai đầu đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn AM gồm điện trở thuần $R=100\sqrt{3}\Omega $ mắc nói tiếp với cuộn cảm thuần có độ tự cảm L, đoạn MB chỉ có tụ điện có điện dung $C=0,05/\pi (mF).$ Biết điện áp giữa hai đầu đoạn mạch MB và điện áp giữa hai đầu đoạn mạch AB lệch pha nhau $\pi /3.$ Gía trị L bằng:

A. $2/\pi (H).$ B. $1/\pi (H).$ C. $\sqrt{3}/\pi (H).$ D. $3/\pi (H).$

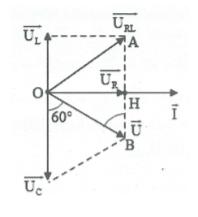HD giải: Vẽ giản đồ vecto như hình vẽ bên.

Ta có: $\widehat{{{U}_{C}}OB}=\widehat{OBA}={{60}^{0}}.$

Suy ra $HB\tan B=OH\Rightarrow HB=\frac{R}{\sqrt{3}}=100.$

Mặt khác ${{Z}_{C}}=\frac{1}{C\omega }=200\Omega \Rightarrow HA=100\Omega ={{Z}_{L}}.$

Do đó $L=\frac{1}{\pi }(H).$ Chọn B.

Bài tập 6: Cho mạch điện RLC. Điện áp đặt hai đầu đoạn mạch có dạng $u=U\sqrt{2}c\text{os}(\omega t)V;{{R}^{2}}=\frac{L}{C}.$ Cho biết điện áp hiệu dụng ${{U}_{RL}}=\sqrt{5}{{U}_{RC}}.$Hệ số công suất của đoạn mạch có giá trị là :

A. $\frac{\sqrt{21}}{5}.$ B. $\frac{\sqrt{5}}{21}.$ C. $\sqrt{\frac{3}{7}}.$ D. $\sqrt{\frac{5}{21}}.$

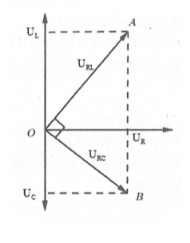HD giải:

Cách 1: Ta có: ${{R}^{2}}=\frac{L}{C}\Rightarrow {{R}^{2}}={{Z}_{L}}{{Z}_{C}}$ nên tam giác

OAB vuông tại O. Chọn

${{U}_{RC}}=I\Rightarrow {{U}_{RL}}=\sqrt{5}\Rightarrow AB=\sqrt{6}.$

Suy ra ${{U}_{R}}=\sqrt{\frac{5}{6}};{{U}_{L}}=\frac{5}{\sqrt{6}};{{U}_{C}}=\frac{1}{\sqrt{6}}$

$\Rightarrow c\text{os}\varphi =\frac{{{U}_{R}}}{\sqrt{U_{R}^{2}+{{({{U}_{L}}-{{U}_{C}})}^{2}}}}=\sqrt{\frac{5}{21}}.$

Cách 2:[Đại số]. Ta có: ${{R}^{2}}=\frac{L}{C}\Rightarrow {{R}^{2}}={{Z}_{L}}.{{Z}_{C}}.$

Lại có: ${{U}_{RL}}=\sqrt{5}{{U}_{RC}}\Rightarrow {{R}^{2}}+Z_{L}^{2}=5({{R}^{2}}+Z_{C}^{2})\Rightarrow 4{{R}^{2}}=Z_{L}^{2}-5Z_{C}^{2}\Leftrightarrow 4{{Z}_{L}}.{{Z}_{C}}=Z_{L}^{2}-5Z_{C}^{2}.$

$\Leftrightarrow ({{Z}_{L}}-5{{Z}_{C}})({{Z}_{L}}+{{Z}_{C}})=0\Rightarrow {{Z}_{L}}=5{{Z}_{C}}$

$\Rightarrow c\text{os}\varphi =\frac{R}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}=\frac{R}{\sqrt{{{R}^{2}}+16Z_{C}^{2}}}=\frac{R}{\sqrt{{{R}^{2}}+\frac{16}{5}}{{R}^{2}}}.$Do đó $c\text{os}\varphi =\frac{\sqrt{5}}{21}.$Chon D.

Bài tập 7: Một mạch điện gồm cuộn cảm có độ tự cảm L và điện trở thuần r mắc nối tiếp với tụ điện có điện dung C thay đổi được. Đặt vào hai đầu mạch một hiệu điện thế xoay chiều có giá trị hiệu dụng U và tần số f không đổi. Khi điều chỉnh để điện dung của tụ điện có giá trị $C={{C}_{1}}$ thì điện áp hiệu dụng giữa hai đầu tụ điện và hai đầu cuộn cảm có cùng gía trị và bằng U, cường độ dòng điện trong mạch khi có biểu thức ${{i}_{1}}=2\sqrt{6}c\text{os}(100\pi t+\pi /4)(A).$Khi điều chỉnh để điện dung của tụ điện có giá trị $C={{C}_{2}}$thì điện áp hiệu dụng giữa hai bản tụ điện đạt giá trị cực đại. Cường độ dòng điện tức thời trong mạch khi đó có biểu thức là:

A. ${{i}_{2}}=2\sqrt{2}c\text{os}(100\pi t+5\pi /12)(A).$ B. ${{i}_{2}}=2\sqrt{3}c\text{os}(100\pi t+5\pi /12)(A).$

C. ${{i}_{2}}=2\sqrt{3}c\text{os}(100\pi t+\pi /3)(A).$ D. ${{i}_{2}}=2\sqrt{2}c\text{os}(100\pi t+\pi /3)(A).$

HD giải: vẽ giản đồ vecto như hình vẽ:

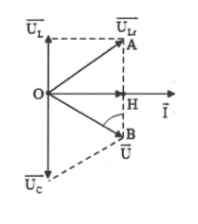Khi $C={{C}_{1}}$ ta có: ${{U}_{Lr}}={{U}_{C}}={{U}_{AB}}$ nên $\Delta OAB$đều.

Suy ra $\widehat{AOH}={{30}^{0}}\Rightarrow \frac{{{Z}_{L}}}{r}=\tan {{30}^{0}}\Rightarrow r={{Z}_{L}}\sqrt{3}.$

Chọn ${{Z}_{L}}=1,r=\sqrt{3}\Rightarrow {{Z}_{Lr}}={{Z}_{C}}=Z=2$

$\Rightarrow U=Z.I=4\sqrt{3}\Rightarrow u=4\sqrt{6}c\text{os}(100\pi t+\pi /12).$

Khi $C={{C}_{2}}$thì ${{U}_{Cm\text{ax}}}$

$\Rightarrow {{Z}_{C2}}=\frac{{{r}^{2}}Z_{L}^{2}}{{{Z}_{L}}}=4\Rightarrow {{I}_{0}}=\frac{{{U}_{0}}}{\sqrt{{{r}^{2}}+{{({{Z}_{L}}-{{Z}_{C2}})}^{2}}}}=\frac{4\sqrt{6}}{\sqrt{3+9}}=2\sqrt{2}.$

$\tan \varphi =\frac{{{Z}_{L}}-{{Z}_{C}}}{r}=-\sqrt{3}\Rightarrow \varphi =-\frac{\pi }{3}\Rightarrow I=2\sqrt{2}c\text{os}(100\pi t+5\pi /12).$ Chọn A.

Dạng 2: Phương pháp vecto trượt

1. Lý thuyết chung và phương pháp giải:

Góc giữa hai vecto: Góc giữa 2 vecto $\overrightarrow{a}$ và $\overrightarrow{b}$

khác $\overrightarrow{0}$được định nghĩa bằng góc $\widehat{AOB}$với

$\overrightarrow{OA}=\overrightarrow{a};\overrightarrow{OB}=\overrightarrow{b}.$

Quy tắc vẽ :

-Chọn ngang là trục dòng điện.

-Chọn điểm đầu mạch A làm gốc.

-Vẽ lần lượt các véc –tơ $\overrightarrow{{{U}_{R}}};\overrightarrow{{{U}_{L}}};\overrightarrow{{{U}_{C}}};\overrightarrow{{{U}_{r}}}$biểu diễn các điện áp, lần lượt từ O sang B nối đuôi nhau liên tiếp theo các nguyên tắc:

Với R; r ta vẽ mũi tên ngang:

Với L ta vẽ bằng mũi tên đi lên:

Với C ta vẽ bằng mũi tên đi xuống:

Độ dài các véc-tơ tỉ lệ với các giá trị hiệu dụng tương ứng.

– Nối các điểm trên giản đồ có liên quan đến dữ kiện của bài toán.

– Biễu diễn các số liệu lên giản đồ.

– Dựa vào các hệ thức lượng trong tam giác để tìm các điện áp hoặc góc chưa biết.

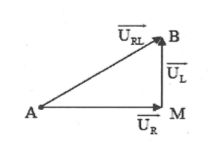2. Minh họa một số mạch thường gặp.

+) Mạch RL. Giản đồ vecto như hình vẽ:

Khi đó $\overrightarrow{{{U}_{C}}}=\overrightarrow{AM},\overrightarrow{{{U}_{L}}}=\overrightarrow{MB},\overrightarrow{{{U}_{RL}}}=\overrightarrow{AB}.$

+) Mạch RC (tương tự).

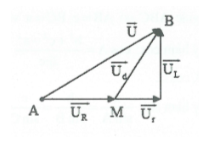
+) Mạch RLr.

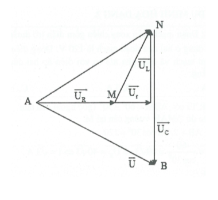+) Mạch R – Lr – C .

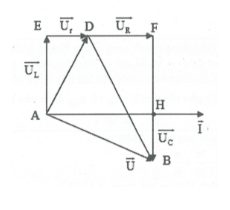+) Mạch Lr – R – C .

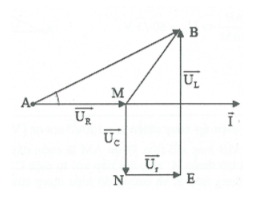+) Mạch R – C – Lr .

3. Công cụ toán học.

Cho tam giác ABC có AB = c, BC = a và CA = b.

+) Định lý hàm cos: $\cos A=\frac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$ tương tự

cho cos B, cos C.

+) Đinh lý hàm sin: $\sin =\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}.$

4. VÍ DỤ MINH HỌA DẠNG 2.

Bài tập 1: Đoạn mạch điện xoay chiều gồm điện trở thuần $R=40\Omega $ mắc nối tiếp với cuộn dây. Điện áp hiệu dụng ở hai đầu đoạn mạch là 120V. Dòng điện trong mạch lệch pha $\pi /6$ so với điện áp hai đầu đoạn mạch và lệch pha $\pi /3$so với điện áp hai đầu cuôn dây. Cường độ hiệu dụng dòng qua mạch bằng :

A. $\sqrt{3}A.$ B. $3A.$ C. $1A.$ D. $\sqrt{2}A.$

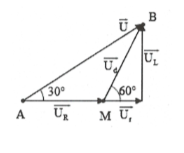HD giải: Ta có: $\widehat{ABM}={{60}^{0}}-{{30}^{0}}$(góc ngoài của tam

giác ). Do đó $\Delta MAB$ vuông cân tại M.

Khi đó: $AB=2AMc\text{os}{{30}^{0}}=120$

$\Rightarrow AM=\frac{60}{c\text{os}{{30}^{0}}}=40\sqrt{3}\Rightarrow {{U}_{R}}=40\sqrt{3}\Rightarrow I=\sqrt{3}A.$

Chọn A.

Bài tập 2: Trên đoạn mạch xoay chiều không phân nhánh có bốn điểm theo đúng thứ tự A, M, N và B. Giữa hai điểm A và M chỉ có điện trở thuần, giữa hai điểm M và N chỉ có tụ điện, giữa hai điểm N và B chỉ có cuộn cảm. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều 240V – 50 Hz thì ${{u}_{MB}}$ và ${{u}_{AM}}$ lệch pha nhau $\pi /3$, ${{u}_{AB}}$ và ${{u}_{MB}}$ lệch pha nhau $\pi /6$. Điện áp hiệu dụng trên R là:

A. $80V.$ B. $60V.$ C. $80\sqrt{3}V.$ D. $60\sqrt{3}V.$

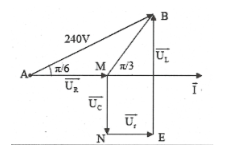HD giải: Xét tam giác AMB ta có:

$\widehat{ABM}=\frac{\pi }{3}-\frac{\pi }{6}=\frac{\pi }{6}.$

Áp dụng định lý hàm sin trong $\Delta AMB$ta

có: $\frac{{{U}_{R}}}{\sin B}=\frac{AB}{\sin M}\Rightarrow {{U}_{R}}=80\sqrt{3}V.$

Chọn C.

Bài tập 3: Đặt điện áp xoay chiều $u=120\sqrt{3}c\text{os}\omega t(V)$ vào hai đầu đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn AM là cuộn dây có điện trở thuần r và có độ tự cảm L, đoạn MB gồm điện trở thuần R mắc nối tiếp với tụ điện C. Điện áp hiệu dụng trên đoạn MB gấp ba lần điện áp hiệu dụng trên R và cường độ hiệu dụng của dòng điện trong mạch là 1 A. Điện áp trên đoạn MB lệch pha so với điện áp hai đầu đoạn mạch là $\pi /2$. Công suất tiêu thụ toàn mạch là:

A. $80\text{W}.$ B. $80\sqrt{2}\text{W}\text{.}$ C. $80\sqrt{3}\text{W}\text{.}$ D. $80\sqrt{6}\text{W}.$

HD giải: Ta có: $\widehat{MBF}=\widehat{BAI}$ (vì cùng phụ

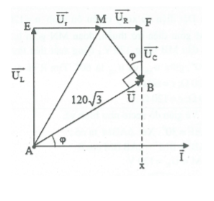với góc $\widehat{ABx}$).

Mặt khác $\sin \varphi =\frac{{{U}_{R}}}{{{U}_{AM}}}=\frac{1}{3}\Rightarrow c\text{os}\varphi =\frac{2\sqrt{2}}{3}.$

Khi đó $P=UIc\text{os}\varphi =\frac{120\sqrt{3}}{\sqrt{2}}.1.\frac{2\sqrt{2}}{3}$

$=80\sqrt{3}\text{W}.$. Chọn C.

Bài tập 4: Đặt điện áp xoay chiều tần số $u={{U}_{0}}c\text{os}100\pi t(V)$vào hai đầu đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn AM gồm điện trở thuần R mắc nối tiếp với cuộn cảm có độ tự cảm L có điện trở trong r, biết rằng $R=2r$, đoạn MB chỉ có tụ điện có điện dung $0,1/\pi $. Biết điện áp giữa hai đầu đoạn dây và điện áp giữa hai đầu đoạn mạc AB lệch pha nhau $\pi /2$và cường độ . Gía trị L bằng:

A. $1/\pi (H).$ B. $0,5/\pi (H).$ C. $2/\pi (H).$ D. $1,2/\pi (H).$

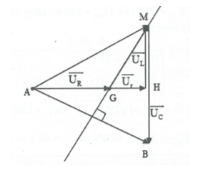HD giải: Vẽ giản đồ vecto như hình vẽ.

Xét tam giác AMB có trọng tâm G đồng thời là

trực tâm nên $\Delta AMB$đều.

Khi đó ${{Z}_{L}}=\frac{{{Z}_{C}}}{2}=50\Omega .$.

Do đó $L=\frac{0,5}{\pi }(H).$ Chọn B.

Bài tập 5: Đặt điện áp xoay chiều $u=100\sqrt{10}c\text{os}100\pi t(V)$ổn định và mạch điện nối tiếp gồm tụ điện có điện dung C, điện trở thuần R và cuộn dây có độ tự cảm L có điện trở thuần r. Khi đó điện áp giữa hai đầu điện trở R là 100V và cường độ dòng điện trong mạch là 0,5(A), biết rằng $L=1/\pi (H)$. Công suất của đoạn mạch là:

A. 43,3W. B. 180,6W. C. 75W. D. 90,3W.

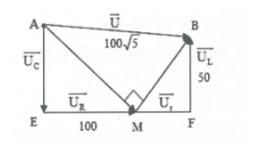HD giải: Vẽ giản đồ vecto như hình vẽ.

Ta có: $\widehat{EAM}=\widehat{BMF}$ (cùng phụ với $\widehat{BMF}$).

Khi đó $\sin \widehat{EAM}=\sin \widehat{BMF}\Rightarrow \frac{100}{x}=\frac{50}{y}.$

(với $AM=x;BM=y$). Lại có: ${{x}^{2}}+{{y}^{2}}=A{{B}^{2}}$.

Suy ra $x=200,y=100$

$\Rightarrow AE=100\sqrt{3},MF=50\sqrt{3}.$

$\Rightarrow {{U}_{R+r}}=100+50\sqrt{3}\Rightarrow P={{U}_{R+r}}.I=90,3\text{W}.$Chọn D.

Bài tập 6: Đặt điện áp xoay chiều ổn định $u=120\sqrt{6}c\text{os}100\pi t(V)$vào hai đầu đoạn mạch AB. Đoạn AM gồm điện trở thuần, đoạn MN gồm tụ điện, đoạn NB chỉ gồm cuộn dây, điện áp hiệu dụng hai đầu MB bằng 120V, công suất tiêu thụ toàn mạch là 360 W, độ lệch pha giữa ${{u}_{AN}}$và ${{u}_{MB}}$ là ${{90}^{0}}$, giữa ${{u}_{AN}}$và ${{u}_{AB}}$là ${{60}^{0}}$.Tìm R và r :

A. $R=120\Omega ;r=60\Omega .$ B.</span

HD giải: Vẽ giản đồ vecto như hình vẽ.

Ta có: $\widehat{ABF}={{30}^{0}}.$ Xét $\Delta ABM$ta có:

$A{{M}^{2}}=A{{B}^{2}}+B{{M}^{2}}-2AB.BM\cos B$

Suy ra $AM={{U}_{R}}=120V.$

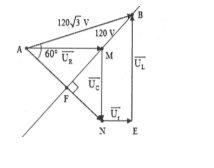
Dễ dàng suy ra $\widehat{AMB}={{120}^{0}}$

$\Rightarrow {{U}_{R}}=BMc\text{os}{{60}^{0}}=60V.$

Mặt khác $P={{U}_{R+r}}.I\Rightarrow I=2A$

$\Rightarrow R=60\Omega ,r=30\Omega .$.Chọn B.

Ví dụ 7: Đặt điện áp xoay chiều $u=160c\text{os}\omega t(V)$vào hai đầu đoạn mạch AB. Đoạn AM gồm điện trở thuần, đoạn MN gồm tụ điện, đoạn NB chỉ gồm cuộn dây, điện áp hiệu dụng ${{U}_{AM}}={{U}_{NB}}=50(V)$và ${{U}_{MN}}=120(V)$, công suất tiêu thụ toàn mạch là 80 W. Điện trở thuần của cuộn dây bằng :

A. $15\Omega .$ B. $30\Omega .$ C. $20\Omega .$ D. $40\Omega .$

HD: Ta có : $\left\{ \begin{array}{} U_{L}^{2}+U_{r}^{2}={{50}^{2}} \\ {} {{(50+{{U}_{r}})}^{2}}+{{({{U}_{L}}-120)}^{2}}=U_{AB}^{2}={{(80\sqrt{2})}^{2}}. \\ \end{array} \right.$

Suy ra: ${{(50+{{U}_{r}})}^{2}}+(\sqrt{2500-U_{r}^{2}}-60)=12800.$

$\xrightarrow[SHIFT-CALC]{X={{U}_{R}}}X={{U}_{r}}=30V\Rightarrow {{U}_{L}}=40V\Rightarrow I=\frac{P}{{{U}_{R+r}}}=1A\Rightarrow r=30\Omega .$.Chọn B.

Ví dụ 8: Đặt điện áp xoay chiều $u=U\sqrt{2}c\text{os}100\pi t(V)$vào hai đầu đoạn mạch AB. Đoạn AM gồm điện trở thuần $R=80\Omega $, đoạn MN gồm cuộn dây không thuần cảm có $r=20\Omega $, đoạn NB chỉ gồm tụ điện, điện áp hiệu dụng ${{u}_{AN}}=300V,{{u}_{MB}}=60\sqrt{3}V$. Biết ${{u}_{AN}}$và ${{u}_{AB}}$vuông pha với nhau.Điện áp hiệu dụng hai đầu mạch có giá trị gần bằng :

A. 200V B. 120V C. 275V D. 180V

HD giải: Vẽ giản đồ vecto như hình vẽ bên.

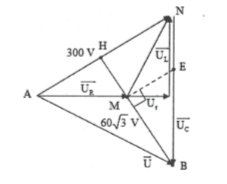
Dựng $MB//AN$. Khi đó theo Talet ta có:

$\frac{r}{R+r}=\frac{ME}{AN}\Rightarrow ME=\frac{1}{5}AN=60.$

Mặt khác $MB\bot AN\Rightarrow \Delta MEB$vuông tại M.

Áp dụng hệ thức lượng ta có:

$\frac{1}{U_{r}^{2}}=\frac{1}{M{{E}^{2}}}+\frac{1}{M{{B}^{2}}}\Rightarrow {{U}_{r}}=30\sqrt{3}V$

$\Rightarrow {{U}_{R}}=4{{U}_{r}}=120\sqrt{3}V.$

${{U}_{C}}-{{U}_{L}}=\sqrt{M{{B}^{2}}-U_{r}^{2}}=90V.$

$\Rightarrow AB=\sqrt{{{\left( 150\sqrt{3} \right)}^{2}}+{{90}^{2}}}\approx 275V.$ Chọn C.

Ví dụ 9: Trên mạch điện xoay chiều không phân nhánh AB, giữa AM chỉ có điện trở thuần, giữa MN chỉ có cuộn dây, giữa NB chỉ có tụ điện. Cuộn dây có điện trở thuần r = 0,5R. Điện áp hiệu dụng trên AN là $U\sqrt{3}$ và trên đoạn MB là U. Điện áp tức thời trên đoạn AN và MB vuông pha với nhau. Điện áp tức thời trên AN sớm pha hơn dòng điện là:

A. ${{60}^{0}}$ B. ${{45}^{0}}$ C. ${{30}^{0}}$ D. ${{25}^{0}}$

HD giải: Vẽ giản đồ vecto như hình vẽ bên.

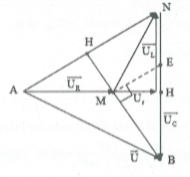
Dựng ME//AN.

Khi đó theo Talet ta có:

$\frac{r}{R+r}=\frac{ME}{AN}=\frac{r}{3r}\Rightarrow ME=\frac{U\sqrt{3}}{3}.$

Xét tam giác MEB vuông tại M.

Suy ra tan $\widehat{MEB}=\frac{MB}{ME}=\sqrt{3}\Rightarrow \widehat{MEB}={{60}^{0}}$

Do đó $\widehat{EMH}={{30}^{0}}$. Chọn C.

Ví dụ 10: [Trích đề thi THPT Thị Xã Quảng trị] Đặt điện áp xoay chiều có biểu thức $u=U\sqrt{2}c\text{os}\omega t(V)$ vào 2 đầu đoạn mạch AB nối tiếp mắc theo thứ tự R, L, C (trong đó L là cuộn cảm thuần). Biết dòng điện tức thời trong mạch trễ pha hơn u, điện áp hiệu dụng hai đầu đoạn mạch chứa R và L có giá trị bằng $U\sqrt{3}$ và sớm pha hơn u góc ${{30}^{0}}$. Hệ số công suất của đoạn mạch AB là:

A. $\frac{\sqrt{3}}{3}$ B. $\frac{\sqrt{3}}{2}$ C. $\frac{\sqrt{5}}{2}$ D. $\frac{\sqrt{2}}{2}$

HD giải:

Áp dụng định lý hàm số cos cho $\Delta OMN$:

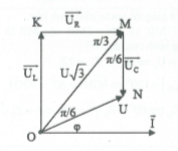
$U_{c}^{\text{2}}={{U}^{2}}+(U\sqrt{3)}c\text{os}{{30}^{0}}-2{{U}^{2}}\sqrt{3}c\text{os}{{30}^{0}}=U.$

$\Rightarrow \Delta OMN$cân tại N có góc $\widehat{OMN}={{30}^{0}}$.

Do đó $\widehat{OMK}={{60}^{0}}\Rightarrow {{U}_{R}}=OM\cos {{60}^{0}}=\frac{U\sqrt{3}}{2}$

$\Rightarrow {{U}_{L}}=OM\sin {{60}^{0}}=\frac{3U}{2}\Rightarrow c\text{os}\varphi =\frac{{{U}_{R}}}{U}$

$=\frac{{{U}_{R}}}{\sqrt{U_{R}^{2}+{{({{U}_{L}}-{{U}_{C}})}^{2}}}}=\frac{\sqrt{3}}{2}$. Chọn B.

Ví dụ 11: [Trích đề thi THPT Thị Xã Quảng trị] Đặt điện áp xoay chiều có giá trị hiệu dụng U = 240 V, tần số 50 Hz vào A, B của mạch điện gồm 3 AM, MN, NB mắc nối tiếp. Đoạn AM chứa điện trở thuần, MN chứa cuộn dây có độ tự cảm $L=\frac{6}{5\pi }H$ và NB chứa tụ điện. Các điện áp hiệu dụng ${{U}_{AM}}=150(V)$, ${{U}_{AN}}=240V$, độ lệch pha giữa các điện áp ${{U}_{MN}}$ với ${{U}_{AM}}$ và ${{U}_{AN}}$ với ${{U}_{AB}}$ có độ lớn bằng nhau. Nối tắt cuộn dây thì công suất tiêu thụ của mạch là:

A. 118 W. B. 108 W. C. 98 W. D. 96 W.

HD giải: Dựng giản đồ vecto như hình vẽ.

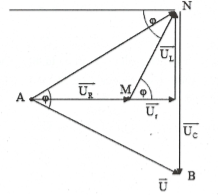
Ta có: ${{U}_{AN}}={{U}_{AB}}$ nên tam giác ANB cân tại A

Suy ra AM là đường cao đồng thời là phân giác

$\Rightarrow \widehat{NAM}=\frac{\varphi }{2}\widehat{ANM}\Rightarrow \Delta AMN$ cân tại

M$\Rightarrow {{U}_{AM}}={{U}_{MN}}=150V$.

Mặt khác: $c\text{os}\frac{\varphi }{2}=\frac{{{U}_{MN}}/2}{{{U}_{AM}}}=0,8$

$\Rightarrow c\text{os}\varphi =2{{\cos }^{2}}\frac{\varphi }{2}-1=0,28\Rightarrow {{U}_{L}}={{U}_{MN}}\sin \varphi $.

$={{U}_{MN}}\sqrt{1-c\text{o}{{\text{s}}^{2}}\varphi }=144V$

Dòng điện hiệu dụng trong mạch $I=\frac{{{U}_{L}}}{{{Z}_{L}}}=\frac{144}{120}=1,2A\Rightarrow R=\frac{150}{1,2}=125\Omega .$

Do ${{Z}_{C}}=2{{Z}_{L}}=250\Omega \Rightarrow $Khi nối tắt cuộn dây thì công suất tiêu thụ trong mạch là

$P=\frac{{{U}^{2}}}{R}.c\text{o}{{\text{s}}^{2}}\varphi ‘=\frac{{{240}^{2}}}{125}.\frac{{{125}^{2}}}{{{125}^{2}}+{{240}^{2}}}=98W.$Chọn C.

Ví dụ 12: [Trích đề thi Sở GD-ĐT Hà Nội 2017]

Đặt điện áp xoay chiều vào hai đầu đoạn mạch AB như hình vẽ. Biểu thức điện áp giữa hai đầu các đoạn mạch AN, MB và NB lần lượt là ${{U}_{AN}}=2\sqrt{2}U\cos (\omega t+\varphi );{{u}_{MB}}=\sqrt{2}Uc\text{os}(\omega t+\varphi )$ và ${{U}_{NB}}=U’c\text{os}(\omega t+\varphi -\frac{2\pi }{3})$ . Biết điện trở có giá trị R, cuộn dây có điện trở r và cảm kháng ${{Z}_{L}}$; tụ điện có dung kháng ${{Z}_{C}}$.Hệ thức nào sau đây sai?

A.R = 2r B. $r=\sqrt{3}{{Z}_{C}}$. C. $2R=\sqrt{3}{{Z}_{L}}$. D. ${{Z}_{L}}=2{{Z}_{C}}$.

HD giải: Vẽ giản đồ vecto như hình bên.

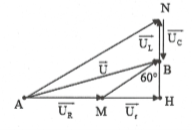
Ta có: AN//MB và AN = 2MB nên MB là

Đường trung bình của$\Delta ANH$

Suy ra ${{U}_{R}}={{U}_{r}}\Rightarrow R=r,{{Z}_{L}}=2{{Z}_{C}}$.

Do$(\widehat{{{u}_{NB}};{{u}_{MB}}})={{120}^{0}}\Rightarrow \widehat{MBH}={{60}^{0}}=\widehat{ANH}$

$\Rightarrow R+r={{Z}_{L}}\tan {{60}^{0}}={{Z}_{L}}\sqrt{3}=2R\Rightarrow r={{Z}_{C}}\sqrt{3}.$

Chọn A.

Ví dụ 13:Mạch điện xoay chiều AB gồm một cuộn dây không cảm thuần, một điện trở thuần và một tụ điện, mắc nối tiếp theo thức tự đã nêu. Điểm M giữa cuộn dây và điện trở thuần. Đặt vào hai đầu mạch điện áp xoay chiều có tần số không đổi và giá trị hiệu dụng 200V thì trong mạch có cộng hưởng điện. Lúc đó điện áp hiệu dụng trên đoạn AM là 160V, độ lệch pha giữa điện áp hai đầu AM so với cường độ dòng điện trong mạch gấp đôi độ lệch pha giữa cường độ dòng điện so với điện áp hai đầu Mb. Điện áp hiệu dụng hai đầu MB là:

A. 120V B. 180V C. 220V D. 240V

HD giải: Phương pháp giản đồ vecto

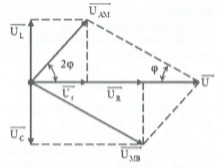
Áp dụng định lý sin trong tam giác ta có:

$\frac{{{U}_{{}}}}{\sin (180-3\varphi )}=\frac{{{U}_{AM}}}{\sin \varphi }$

Tương đương với phương trình:

$\sin 3\varphi -\frac{5}{4}\sin \varphi =0\Rightarrow 4{{\sin }^{3}}\varphi -\frac{7}{4}\sin \varphi =0.$

Giải phương trình trên ta thu được $\sin \varphi \frac{\sqrt{7}}{4}.$

Áp dụng định lý sin ta thu được ${{U}_{MB}}=240V$.Chọn D.

Ví dụ 14: Đặt điện áp xoay chiều AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Điện áp ở hai đầu đoạn mạch ổn định và có biểu thức $u=220\sqrt{2}c\text{os}(100\pi t)V$. Điện áp ở hai đầu đoạn mạch AM sớm pha hơn cường độ dòng điện một góc$\frac{\pi }{6}.$ Đoạn mạch MB chỉ chứa tụ điện có điện dung C thay đổi được. Điều chỉnh C để tổng điện áp hiệu dụng ${{U}_{AM}}+{{U}_{MB}}$có giá trị lớn nhất. Khi đó điện áp hiệu dụng ở hai đầu tụ điện có giá trị:

A. $220\sqrt{3}V$ B. 440V C. $220\sqrt{2}V$ D. $220V$

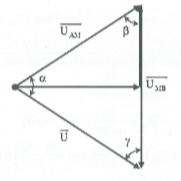
HD giải: Ta có $\frac{U}{\sin \beta }=\frac{{{U}_{AM}}}{\sin \gamma }=\frac{{{U}_{MB}}}{\sin \alpha }.$

$\Rightarrow {{U}_{AM}}+{{U}_{MB}}=\frac{U}{\sin \beta }(\sin \alpha +\sin \gamma )$

Mặt khác: $\sin \alpha +\sin \gamma =2\sin (\frac{\pi -\beta }{2})c\text{os}(\frac{\alpha -\gamma }{2})$

Vậy ${{({{U}_{AM}}+{{U}_{MB}})}_{m\text{ax}}}$ khi $\alpha =\gamma $.

Hơn nữa $\beta =\frac{\pi }{6}\Rightarrow $tam giác đều U = 220V. Chọn D.

Ví dụ 15: Đặt điện áp xoay chiều sản ra công suất cơ học 7,5 kW và có hiệu suất 80%. Mắc động cơ nối tiếp với một cuộn cảm rồi mắc chúng vào mạng điện xoay chiều. Gía trị hiệu điện thế hiệu dụng ở hai đầu động cơ là ${{U}_{M}}$ biết rằng dòng điện qua động cơ có cường độ hiệu dụng I = 40 A và trễ pha với ${{u}_{M}}$một góc $\pi /6$.Hiệu điện thế ở hai đầu cuộn cảm ${{U}_{L}}=125V$và sớm pha so với dòng điện qua cuộn cảm là $\pi /3$. Điện áp hiệu dụng của mạng điện và độ lệch pha của nó so với dòng điện có giá trị tương ứng là:

A. $384V;{{45}^{0}}$ B. $834V;{{45}^{0}}$ C. $384V;{{39}^{0}}$ D. $184V;{{39}^{0}}$

HD giải:

+) Phương pháp giản đồ vecto. Ta có thể đơn giản hóa động cơ

điện gồm cuộn cảm và điện trở trong.

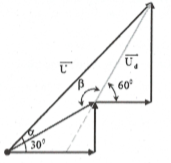
Hiệu suất của động cơ:

$H=\frac{A}{P}\Leftrightarrow 0,8=\frac{7500}{{{U}_{M}}.40.c\text{os}({{30}^{0}})}\Rightarrow {{U}_{M}}=271V$

+) Áp dụng định lý cos trong tam giác ta có

$U=\sqrt{U_{M}^{2}+U_{d}^{2}-2{{U}_{M}}{{U}_{d}}c\text{os}\beta }$

$\Rightarrow U=\sqrt{{{271}^{2}}+{{125}^{2}}-2.271.125.c\text{os}{{150}^{0}}}\approx 384V$

Áp dụng định lý sin trong tam giác ta có:

$\frac{U}{\sin \beta }=\frac{{{U}_{d}}}{\sin \alpha }\Leftrightarrow \frac{271}{\sin {{150}^{0}}}=\frac{125}{\sin \alpha }\Rightarrow \alpha ={{9}^{0}}$

Vậy độ lệch pha giữa điện áp hai đầu mạch là $\varphi ={{30}^{0}}+\alpha ={{39}^{0}}.$Chọn C.

Ví dụ 16: Đặt một điện áp $u=220\sqrt{2}c\text{os}(100\pi t+\varphi )V$vào hai đầu đoạn mạch AB chứa RLC nối tiếp theo đúng thứ tự đó, điện dung C thay đổi sao cho dòng điện qua mạch có biểu thức $i={{I}_{0}}c\text{os}(100\pi t)A$. Gọi M là một điểm nối giữa cuộn cảm L và tụ điện C. Biết biểu thức điện áp giữa hai đầu đoạn mạch AM, MB lần lượt là ${{u}_{1}}={{U}_{01}}c\text{os}\left( 100\pi t+\frac{\pi }{3} \right)V,$${{u}_{2}}={{U}_{02}}c\text{os}\left( 100\pi t-\frac{\pi }{2} \right)V$. Tổng $({{U}_{01}}+{{U}_{02}})$ có giá trị lớn nhất là

A. 750 V. B. 1202 V. C. 1247 V. D. 1242 V.

HD giải: Áp dụng định lý sin trong tam giác ta có

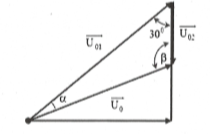
$\frac{{{U}_{01}}}{\sin \beta }=\frac{{{U}_{02}}}{\sin \alpha }=\frac{{{U}_{0}}}{\sin {{30}^{0}}}$

$\Rightarrow {{U}_{01}}+{{U}_{02}}=\frac{{{U}_{0}}}{\sin {{30}^{0}}}(\sin \alpha +\sin \beta )$

${{({{U}_{01}}+{{U}_{02}})}_{m\text{ax}}}=\frac{2{{U}_{0}}}{\sin {{30}^{0}}}\sin \left( \frac{180-30}{2} \right)\approx 1202V.$Chọn B.

Ví dụ 17: Đặt điện áp $u=U\sqrt{2}c\text{os}\omega tV$ (${{U}_{0}}$không đổi) vào hai đầu đoạn mạch gồm cuộn dây và tụ điện mắc nối tiếp. Biết cuộn dây có hệ số công suất bằng 0,97 và tụ điện có điện dung C thay đổi được. Điều chỉnh C để tổng điện áp hiệu dụng trên tụ điện và cuộn dây có giá trị lớn nhất. Khi đó tỉ số giữa cảm kháng và dung kháng của mạch điện có giá trị gần giá trị nhất nào sau đây?

A. 0,26 B. 0,86 C. 0,52 D. 0,71

HD giải: Áp dụng định lý sin trong tam giác ta có

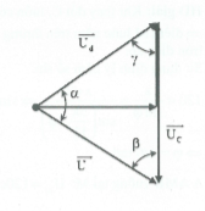
$\frac{{{U}_{d}}}{\sin \beta }=\frac{{{U}_{C}}}{\sin \alpha }=\frac{U}{\sin \gamma }\Rightarrow {{U}_{d}}+{{U}_{C}}=\frac{U}{\sin \gamma }\text{ }\!\![\!\!\text{ }\sin \alpha +\sin \beta \text{ }\!\!]\!\!\text{ }$

Biến đổi lượng giác

$\sin \alpha +\sin \beta =2\sin \left( \frac{\alpha +\beta }{2} \right)c\text{os}\left( \frac{\alpha -\beta }{2} \right)$

$\Rightarrow {{\left( {{U}_{d}}+{{U}_{C}} \right)}_{m\text{ax}}}$khi $c\text{os}\left( \frac{\alpha -\beta }{2} \right)=1\Rightarrow \alpha =\beta $

Từ đó ta có : ${{Z}_{C}}=\sqrt{Z_{L}^{2}+{{r}^{2}}}$

Mặt khác $c\text{os}{{\varphi }_{d}}=\frac{r}{\sqrt{Z_{L}^{2}+{{r}^{2}}}}=0,97$

Chuẩn hóa $r=1\Rightarrow \left\{ \begin{array}{} {{Z}_{L}}=0,25 \\ {} {{Z}_{C}}=1,03 \\ \end{array} \right.\Rightarrow \frac{{{Z}_{C}}}{{{Z}_{L}}}=0,2425$.Chọn A

Ví dụ 18: Đặt điện áp $u=120\sqrt{2}c\text{os}\omega tV$vào hai đầu đoạn mạch AB mắc nối tiếp gồm đoạn mạch AM, MN và NB mắc nối tiếp (theo đúng thứ tự trên). Đoạn mạch AM là cuộn dây, đoạn mạch MN là điện trở R và đoạn mạch NB là tụ điện. Biết ${{U}_{AN}}=120V;{{U}_{MN}}=40\sqrt{3}$. Khoảng thời gian ngắn nhất từ lúc điện áp hai đầu đoạn mạch AM cực đại đến lức cường độ dòng điện trong mạch cực đại bằng khoảng thời gian ngắn nhất từ lúc điện áp hai đầu AN cực đại đến lúc điện áp u cực đại và bằng t. Khoảng thời gian ngắn nhất từ lúc điện áp hai đầu đoạn mạch AN cực đại đến lúc điện áp hai đầu đoạn NB cực đại là

A. 2t B. 4t C. 3t D. 5t

HD giải: Phương pháp giản đồ vecto

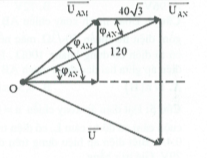
Ta có : $\left| {{\varphi }_{AB}} \right|=\left| {{\varphi }_{AN}} \right|\Rightarrow \frac{{{Z}_{C}}-{{Z}_{L}}}{R+r}=\frac{{{Z}_{L}}}{R+r}\Rightarrow {{Z}_{C}}=2{{Z}_{L}}$

Khoảng thời gian ngắn nhất từ lúc điện áp hai đầu đoạn mạch

AM cực đại đến lúc cường độ dòng điện trong mạch cực đại

bằng khoảng thời gian ngắn nhất từ lúc điện áp hai đầu AN

cực đại đến lúc điện áp u cực đại $\Rightarrow {{\varphi }_{AM}}=2{{\varphi }_{AN}}$

Từ hình vẽ ta thấy được $O{{U}_{AN}}{{U}_{AM}}$ là tam giác cân

$c\text{os}{{\varphi }_{AN}}=\frac{U}{2{{U}_{MN}}}\Rightarrow {{\varphi }_{AN}}=\frac{\pi }{6}$

Khoảng thời gian t từ lúc ${{U}_{AM}}$ cực đại đến khi dòng trong mạch cực đại ứng với độ lệch pha $\pi /3$

${{u}_{AN}}$ sớm pha hơn ${{u}_{NB}}$ một góc $\frac{2\pi }{3}\Rightarrow $khoảng thời gian tương ứng trên là 2t. Chọn C.

Ví dụ 19: Đặt điện áp xoay chiều có giá trị hiệu dụng không đổi $u=120\sqrt{2}c\text{os}(100\pi t)V$vào đoạn mạch AB gồm đọan AM chỉ chứa điện trở R, đoạn mạch MB chứa tụ điện có điện dung C thay đổi được mắc nối tiếp với một cuộn cảm thuần. Biết sau khi thay đổi C thì điện áp hiệu dụng hai đầu đoạn mạch MB tăng$\sqrt{2}$ lần và dòng điện tức thời trong mạch trước và sau khi thay đổi C lệch pha nhau một góc $5\pi /12$. Điện áp hiệu dụng hai đầu mạch AM khi chưa thay đổi C có giá trị bằng

A. $60\pi \sqrt{3}V$ B. $120V$ C. $60V$ D. $60\sqrt{2}V$

HD giải: Khi thay đổi C, luôn có: ${{U}_{R}}\bot {{U}_{CL}}$ và U không đổi

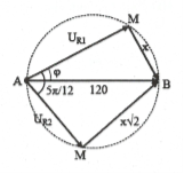
$\Rightarrow $điểm M luôn nằm trên đường tròn có bán kính AB. Ta có đường

tròn điện áp:

Sử dụng định lý hàm số sin:

$120=\frac{x}{\sin \varphi }=\frac{x\sqrt{2}}{\sin \left( \frac{5\pi }{12}-\varphi \right)}\Rightarrow \sin \left( \frac{5\pi }{12}-\varphi \right)=\sqrt{2}\sin \varphi $

$\Rightarrow \varphi =\pi /6rad$

$\Delta AMB$ vuông tại M: ${{U}_{R1}}=120c\text{os}\frac{\pi }{6}=60\sqrt{3}V.$Chọn A.

LÝ THUYẾT TRỌNG TÂM, PHƯƠNG PHÁP GIẢI VÀ BÀI TẬP GIẢN ĐỒ VECTƠ

Dạng 1. Phương pháo vecto buộc (vecto chung gốc)

Lý thuyết chung và phương pháp giải:

VÍ DỤ MINH HỌA DẠNG 1.

Dạng 2: Phương pháp vecto trượt

1. Lý thuyết chung và phương pháp giải:

2. Minh họa một số mạch thường gặp.

3. Công cụ toán học.

4. VÍ DỤ MINH HỌA DẠNG 2.

Bài liên quan:

Leave a Comment Hủy