I. LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
1. Khảo sát mạch R-L-C (cuộn dây thuần cảm)
Tổng quát:
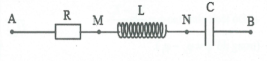Giả sử dòng diện trong mạch có biểu thức
là: $i={{I}_{0}}\cos \omega t$
Suy ra:$\left\{ \begin{array}{} {{u}_{R}}={{U}_{0R}}\cos \omega t \\ {} {{u}_{L}}={{u}_{0L}}\cos \left( \omega t+\frac{\pi }{2} \right)\Rightarrow u={{u}_{R}}+{{u}_{L}}+{{u}_{C}} \\ {} {{u}_{C}}={{u}_{0C}}\cos \left( \omega t-\frac{\pi }{2} \right) \\ \end{array} \right.$ .
Đặc điểm:
|
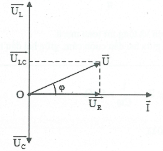
TH 1: ${{Z}_{L}}>{{Z}_{C}}$ |
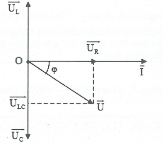
TH 2: ${{Z}_{L}}<{{Z}_{C}}$ |
|
|
|
+) Điện áp: ${{U}^{2}}=U_{R}^{2}+U_{LC}^{2}=U_{R}^{2}+{{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}\Rightarrow U=\sqrt{U_{R}^{2}+{{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}}$ .
+) Tổng trở: $Z=\frac{U}{I}=\frac{\sqrt{U_{R}^{2}+{{({{U}_{L}}-{{U}_{C}})}^{2}}}}{I}=\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}$ .
+) Định luật Ôm: $I=\frac{U}{Z}=\frac{{{U}_{R}}}{R}=\frac{{{U}_{C}}}{{{Z}_{C}}}=\frac{{{U}_{L}}}{{{Z}_{L}}}=\frac{{{U}_{RL}}}{{{Z}_{RL}}}=..$.
+) Độ lệch pha: $\varphi ={{\varphi }_{u}}-{{\varphi }_{i}}$ ta có:$\tan \varphi =\frac{{{U}_{LC}}}{{{U}_{R}}}=\frac{{{U}_{L}}-{{U}_{C}}}{{{U}_{R}}}=\frac{{{Z}_{L}}-{{Z}_{C}}}{R}$ .
Nếu ${{Z}_{L}}>{{Z}_{C}}$ : Mạch có tính cảm kháng (khi đó u sớm pha hơn i).
Nếu ${{Z}_{L}}<{{Z}_{C}}$ : Mạch có tính dung kháng (khi đó u chậm pha hơn i).
Chú ý: Để viết biểu thức của các điện áp thành phần ta nên so sánh độ lệch của nó với pha của dòng điện.
2. Khảo sát mạch R-Lr-C khi cuộn dây không thuần cảm
Tổng quát:
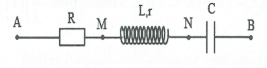
Đặt ${{R}_{Rr}}=R+r$ là tổng trở thuần
của mạch. Khi đó:
+) Điện áp: ${{U}^{2}}=U_{LC}^{2}+U_{Rr}^{2}$
$=\left( {{U}_{L}}-{{U}_{C}} \right)+{{\left( {{U}_{R}}+{{U}_{r}} \right)}^{2}}$
+) Tổng trở của mạch:
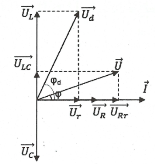
$Z=\sqrt{{{\left( R+r \right)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}$.
+) Định luật Ôm:
$I=\frac{U}{Z}=\frac{{{U}_{R}}}{R}=\frac{{{U}_{r}}}{r}=\frac{{{U}_{L}}}{{{Z}_{L}}}=\frac{{{U}_{C}}}{{{Z}_{C}}}=…$
+) Độ lêch pha: $\tan \varphi =\frac{{{Z}_{L}}-{{Z}_{C}}}{R+r}$
(trong đó $\varphi ={{\varphi }_{u}}-{{\varphi }_{i}}$).
VÍ DỤ MINH HỌA
|
Bài tập minh họa: Mạch điện xoay chiều gồm một điện trở thuần$R=40\Omega $, một cuộn thuần cảm có hệ số tự cảm $L=\frac{0,8}{\pi }\left( H \right)$và một tụ điện có điện dung $C=\frac{{{2.10}^{-4}}}{\pi }\left( F \right)$ mắc nối tiếp. Biết rằng dòng điện qua mạch có dạng $i=3\cos 100\pi t\left( A \right).$ a) Tính cảm kháng của cuộn cảm, dung kháng của tụ điện và tổng trở toàn mạch. b) Viết biểu thức điện áp tức thời giữa hai đầu điện trở, giữa hai đầu cuộn cảm, giữa hai đầu tụ điện, giữa hai đầu mạch điện. |
HD giải:
a) Cảm kháng: ${{Z}_{L}}=L\omega =100\pi .\frac{0,8}{\pi }=80\Omega .$Dung kháng: ${{Z}_{C}}=\frac{1}{C\omega }=50\Omega .$
Tổng trở: $Z=\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=\sqrt{{{40}^{2}}+{{\left( 80-50 \right)}^{2}}}=50\Omega .$
b) Vì ${{u}_{R}}$cùng pha với i nên: ${{u}_{R}}={{U}_{0R}}\cos 100\pi t$với ${{U}_{0R}}={{I}_{0}}.R=3.40=120V.$
Vậy $u=120\cos 100\pi t\left( V \right).$
Vì ${{u}_{L}}$nhanh pha hơn i góc $\frac{\pi }{2}$nên: ${{u}_{L}}={{U}_{0L}}\cos \left( 100\pi t+\frac{\pi }{2} \right)$
với ${{U}_{0L}}={{I}_{0}}.{{Z}_{L}}=3.80=240V.$Vậy ${{u}_{L}}=240\cos \left( 100\pi t+\frac{\pi }{2} \right)\left( V \right).$
Vì ${{u}_{C}}$chậm pha hơn i góc $\frac{-\pi }{2}$nên: ${{u}_{C}}={{U}_{0C}}\cos \left( 100\pi t-\frac{\pi }{2} \right)$
${{U}_{0C}}={{I}_{0}}{{Z}_{C}}=3.50=150V.$ Vậy ${{u}_{C}}=150\cos \left( 100\pi t-\frac{\pi }{2} \right)\left( V \right).$
Áp dụng công thức: $\tan \varphi =\frac{{{Z}_{L}}-{{Z}_{C}}}{R}=\frac{3}{4}\Rightarrow \varphi \approx 0,2\pi \left( rad \right).$
$\Rightarrow $ biểu thức hiệu điện thế tức thời giữa hai đầu mạch điện: $u={{U}_{0}}\cos \left( 100\pi t+\varphi \right)$
Với ${{U}_{0}}={{I}_{0}}Z=150V.$ Vậy $u=150\cos \left( 100\pi t+0,2\pi \right)\left( V \right).$
