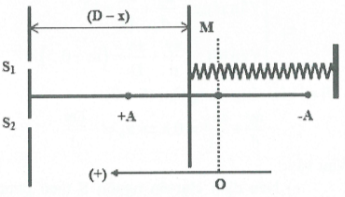
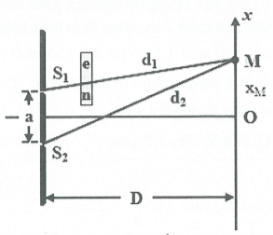
DẠNG 1: BÀI TOÁN VỀ KHOẢNG VÂN; VỊ TRÍ VÂN SÁNG, VÂN TỐI
PHƯƠNG PHÁP GIẢI
– Hiệu đường đi từ hai khe tới M: ${{d}_{1}}-{{d}_{2}}=\frac{ax}{D}$
– Khoảng vân: $i=\frac{\lambda D}{a}$
+) Thực tế: $i\,\,\left( mm \right);\lambda \,\left( \mu m \right);\text{ }a\,\left( mm \right);\text{ }D\,\left( m \right)\Rightarrow i=\frac{\lambda D}{a}=\frac{\left( \mu m \right).(m)}{(mm)}=\frac{{{10}^{-6}}.1}{{{10}^{-3}}}={{10}^{-3}}\Leftrightarrow (mm)$
+) Khoảng cách giữa vân sáng và vân tối liền kề là $\frac{i}{2}$.
+) Trên MN có n vân sáng hoặc n vân tối liên tiếp thì có $\left( n-1 \right)$ khoảng vân: $MN=\left( n-1 \right)i$
– Vân sáng: ${{x}_{s}}=k\frac{\lambda D}{a}=ki\,\,\left( \Leftrightarrow {{x}_{s}}=\pm i,\pm 2i,\pm 3i,… \right)$
– Vân tối: ${{x}_{t}}=\left( k+0,5 \right)\frac{\lambda D}{a}=\left( k+0,5 \right)i\,\,\,\left( \Leftrightarrow {{x}_{t}}=\pm 0,5i;\pm 1,5i;… \right)$
– Để kiểm tra lại M là vân sáng hay vân tối, ta căn cứ vào:
+) Nếu cho tọa độ $\frac{{{x}_{M}}}{i}=\left\{ \begin{array}{} \\ {} \\ \end{array} \right.$
+) Nếu cho hiệu đường đi $\frac{\Delta d}{\lambda }=\frac{{{d}_{2}}-{{d}_{1}}}{\lambda }=\left\{\begin{array}{} \\ {} \\ \end{array} \right.$
– Vân tối thứ k nằm giữa vân sáng bậc (k – 1) và vân sáng bậc k.
– Khoảng cách giữa hai vân m, n bất kỳ trên màn: $\Delta x=\left| {{x}_{m}}-{{x}_{n}} \right|$
VÍ DU MINH HỌA
|
Ví dụ 1: [Trích đề thi THPT QG năm 2007] Trong thí nghiệm Y-âng về giao thoa của ánh sáng đơn sắc, hai khe hẹp cách nhau 1 mm, mặt phẳng chứa hai khe cách màn quan sát 1,5 m. Khoảng cách giữa 5 vân sáng liên tiếp là 3,6 mm. Bước sóng của ánh sáng dùng trong thí nghiệm này bằng A. 0,48 $\mu m$. B. 0,40 $\mu m$. C. 0,60 $\mu m$. D. 0,76 $\mu m$. |
Lời giải:
5 vân sáng liên tiếp có 4 khoảng vân: $4i=3,6\Rightarrow i=0,9$mm.
$\Rightarrow $Bước sóng $\lambda =\frac{ai}{D}=\frac{{{10}^{-3}}.0,{{9.10}^{-3}}}{1,5}=0,{{6.10}^{-6}}$(m). Chọn C.
|
Ví dụ 2: Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa 2 khe là 2 mm; khoảng cách từ 2 khe đến màn là 2 m. Nguồn phát ánh sáng đơn sắc có bước sóng 0,64 $\mu m$. Vân sáng bậc 3 và vân tối thứ 3 tính từ vân sáng trung tâm cách vân sáng trung tâm một khoảng lần lượt bằng A. 1,6 mm; 1,92 mm. B. 1,92 mm; 2,24 mm. C. 1,92 mm; 1,6 mm. D. 2,24 mm; 1,6 mm. |
Lời giải:
Khoảng vân: $i=\frac{\lambda D}{a}=\frac{0,64.2}{2}=0,64$mm
Vị trí của vân sáng bậc 3: ${{x}_{s3}}=3i=3.0,64=1,92$mm
Vị trí của vân tối thứ 3: ${{x}_{t3}}=\left( 2+0,5 \right)i=2,5.0,64=1,6$mm. Chọn C.
|
Ví dụ 3: Tiến hành thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là 0,8 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 1,2 m. Biết khoảng cách từ vân sáng trung tâm đến vân tối thứ 5 là 4,32 mm. Bước sóng của ánh sáng trong thí nghiệm là A. 0,45 $\mu m$. B. 0,64 $\mu m$. C. 0,70 $\mu m$. D. 0,55 $\mu m$. |
Lời giải:
Vị trí vân tối thứ 5 (k = 5) là: $x=\left( k+0,5 \right)i=4,5i$
$\Rightarrow i=\frac{x}{4,5}=\frac{4,32}{5,4}=0,96\,mm$
Mà $i=\frac{\lambda D}{a}\Rightarrow \lambda =\frac{ai}{D}=\frac{0,{{8.10}^{-3}}.0,{{96.10}^{-3}}}{1,2}=0,{{64.10}^{-6}}\,m=0,64\,\mu m$. Chọn B.
|
Ví dụ 4: [Trích đề thi THPT QG năm 2010] Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng đơn sắc có bước sóng $\lambda $. Nếu tại điểm M trên màn quan sát có vân tối thứ ba (tính từ vân sáng trung tâm) thì hiệu đường đi của ánh sáng từ hai khe ${{S}_{1}},{{S}_{2}}$ đến M có độ lớn bằng A. $2,5\lambda .$ B. $3\lambda .$ C. $1,5\lambda .$ D. $2\lambda .$ |
Lời giải:
Tại M là vân tối thứ 3 thì hiệu đường đi: ${{d}_{2}}-{{d}_{1}}=\left( 3-0,5 \right)\lambda =2,5\lambda .$ Chọn A.
|
Ví dụ 5: Trong thí nghiệm giao thoa Y-âng, khoảng cách hai khe là 1,2 mm, khoảng cách giữa mặt phẳng chứa hai khe và màn ảnh là 2 m. Người ta chiếu vào khe Y-âng bằng ánh sáng đơn sắc có bước sóng 0,6 $\mu m$. Xét tại hai điểm M và N trên màn có toạ độ lần lượt là 6 mm và 15,5 mm là vị trí vân sáng hay vân tối? A. M sáng bậc 2; N tối thứ 16. B. M sáng bậc 6; N tối thứ 16. C. M sáng bậc 2; N tối thứ 9. D. M tối bậc 2; N tối thứ 9. |
Lời giải:
Khoảng vân: $i=\frac{\lambda D}{a}=\frac{0,{{6.10}^{-6}}.2}{1,{{2.10}^{-3}}}=1$mm
$\Rightarrow \frac{{{x}_{m}}}{i}=6\Rightarrow $M là vân sáng bậc 6 $\Rightarrow \frac{{{x}_{N}}}{i}=15,5\Rightarrow $N là vân tối thứ 16. Chọn B.
|
Ví dụ 6: Trong thí nghiệm Y-âng về giao thoa ánh sáng, nguồn sáng gồm các bức xạ có bước sóng lần lượt là ${{\lambda }_{1}}$ = 720 nm, ${{\lambda }_{2}}$ = 540 nm, ${{\lambda }_{3}}$ = 432 nm và ${{\lambda }_{4}}$ = 360 nm. Tại điểm M trong vùng giao thoa trên màn mà hiệu khoảng cách đến hai khe bằng 1,08$\mu m$ có vân sáng A. bậc 3 của bức xạ ${{\lambda }_{4}}$. B. bậc 3 của bức xạ ${{\lambda }_{3}}$. C. bậc 3 của bức xạ ${{\lambda }_{1}}$. D. bậc 3 của bức xạ ${{\lambda }_{2}}$. |
Lời giải:
$k=\frac{{{d}_{2}}-{{d}_{1}}}{i}=\frac{\Delta d}{i}:$ k nguyên cho vân sáng, k bán nguyên cho vân tối. Ta có:
${{k}_{1}}=\frac{1,{{08.10}^{-6}}}{{{720.10}^{-9}}}=1,5\Rightarrow $vân tối thứ 2 của ${{\lambda }_{1}}$ ${{k}_{2}}=\frac{1,{{08.10}^{-6}}}{{{540.10}^{-9}}}=2\Rightarrow $vân sáng bậc 2 của ${{\lambda }_{2}}$
${{k}_{3}}=\frac{1,{{08.10}^{-6}}}{{{432.10}^{-9}}}=2,5\Rightarrow $vân tối thứ 3 của ${{\lambda }_{3}}$ ${{k}_{4}}=\frac{1,{{08.10}^{-6}}}{{{360.10}^{-9}}}=3\Rightarrow $vân sáng bậc 3 của ${{\lambda }_{4}}$.
Chọn A.
|
Ví dụ 7: Trong thí nghiệm Y-âng về giao thoa với ánh sáng đơn sắc có bước sóng 0,6$\mu m$. Biết khoảng cách giữa hai khe là 0,6 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 0,8 m. Khoảng cách từ vân tối thứ 2 đến vân sáng bậc 7 nằm cùng phía so với vân trung tâm trên màn quan sát bằng A. 5,1 mm. B. 2,7 mm. C. 3,3 mm. D. 5,7 mm. |
Lời giải:
Khoảng vân: $i=\frac{\lambda D}{a}=\frac{0,6.0,8}{0,8}=0,6$mm
Do 2 vân sáng nằm cùng phía nên ${{x}_{t2}}=1,5i;\,\,{{x}_{s7}}=7i$
$\Rightarrow $Khoảng cách giữa hai vân sáng này là:
$\Delta x=\left| {{x}_{s7}}-{{x}_{t2}} \right|=\left| 7i-\left( 1,5i \right) \right|=5,5i=5,5.0,6=3,3\,mm$. Chọn C.
|
Ví dụ 8: Tiến hành thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là 0,6 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 0,8 m. Biết khoảng cách giữa vân sáng bậc 5 và vân sáng bậc 3 nằm về hai phía vân trung tâm bằng 5,6 mm. Bước sóng của ánh sáng dùng trong thí nghiệm là A. 0,425$\mu m$. B. 0,600$\mu m$. C. 0,525$\mu m$. D. 0,575$\mu m$. |
Lời giải:
Vị trí vân sáng bất kỳ là: $x=ki$
Do 2 vân sáng nằm khác phía $\Rightarrow {{x}_{s5}}=5i;\,{{x}_{s3}}=-3i$
$\Rightarrow $Khoảng cách giữa hai vân sáng này là:
$\Delta x=\left| {{x}_{s5}}-{{x}_{s3}} \right|=\left| 5i-\left( -3i \right) \right|=8i=5,6\Rightarrow i=0,8\,mm$
Mà $i=\frac{\lambda D}{a}\Rightarrow \lambda =\frac{ai}{D}=\frac{0,{{6.10}^{-3}}.0,{{8.10}^{-3}}}{0,8}=0,{{6.10}^{-6}}\,m=0,6\,\mu m$. Chọn B.
|
Ví dụ 9: Trong thí nghiệm Y-âng về giao thoa với ánh sáng đơn sắc có bước sóng 0,6$\mu m$. Biết khoảng cách giữa hai khe là 0,6 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 2 m. Trên màn, hai điểm M và N nằm khác phía so với vân sáng trung tâm, cách vân trung tâm lần lượt là 5,0 mm và 8,0 mm. Trong khoảng giữa M và N (không tính M và N) có A. 6 vân sáng và 6 vân tối. B. 5 vân sáng và 6 vân tối. C. 6 vân sáng và 5 vân tối. D. 5 vân sáng và 5 vân tối. |
Lời giải:
Khoảng vân $i=\frac{\lambda D}{a}=\frac{0,{{6.10}^{-6}}.2}{0,{{6.10}^{-3}}}=2\,mm$
Ta có: $\left\{ \begin{array}{} {{k}_{M}}=\frac{{{x}_{M}}}{i}=\frac{5}{2}=2,5 \\ {} {{k}_{N}}=\frac{{{x}_{N}}}{i}=\frac{-8}{2}=-4 \\ \end{array} \right.\Rightarrow -4<k<2,5$
Với k nguyên cho vân sáng $\Rightarrow $6 vân sáng.
k bán nguyên cho vân tối $\Rightarrow $5 vân tối. Chọn C.
|
Ví dụ 10: Trong thí nghiệm Y-âng về giao thoa ánh sáng với bước sóng $\lambda $ = 0,5$\mu m$, khoảng cách giữa hai khe là a = 0,5 mm và khoảng cách từ hai khe đến màn quan sát là D = 2m. Trên màn, khoảng cách giữa một vân sáng và một vân tối cách nhau 3 vân sáng là A. 1 mm. B. 3 mm. C. 5 mm. D. 7 mm. |
Lời giải:
Khoảng vân: $i=\frac{\lambda D}{a}=\frac{0,5.2}{0,5}=2$mm
Khoảng cách giữa vân sáng đến vân tối cạnh nó là 0,5i
$\Rightarrow $ Khoảng cách từ vân sáng đến vân tối cách nó 3 vân sáng là $\Delta x=3i+0,5i=3,5i=7\,mm$.
Chọn D.
|
Ví dụ 11: Trong thí nghiệm giao thoa ánh sáng bằng hai khe Y-âng, khoảng cách hai khe là a, khoảng cách hai khe đến màn là D = 2,4 m. Khi chiếu bức xạ ${{\lambda }_{1}}$ = 0,5$\mu m$ thì giữa 15 vân sáng liên tiếp cách nhau 3 cm, nhưng khi chiếu bức xạ có bước sóng ${{\lambda }_{2}}$ thì trong 3 cm chỉ có 11 vân sáng liên tiếp. Bước sóng của bức xạ ${{\lambda }_{2}}$ là A. 0,6$\mu m$. B. 0,65$\mu m$. C. 0,70$\mu m$. D. 0,72$\mu m$. |
Lời giải:
Đối với bức xạ ${{\lambda }_{1}}$ = 0,5$\mu m$ ta có: $\left( 15-1 \right).{{i}_{1}}=3$
Đối với bức xạ ${{\lambda }_{2}}$ ta cũng có: $\left( 11-1 \right).{{i}_{2}}=3$
Từ 2 phương trình trên ta được: $14{{i}_{1}}=10{{i}_{2}}\Rightarrow {{i}_{2}}=\frac{14}{10}{{i}_{1}}\Rightarrow {{\lambda }_{2}}=\frac{14}{10}{{\lambda }_{1}}=\frac{14}{10}.0,5=0,7\mu m$. Chọn C.
DẠNG 2: BÀI TOÁN TÌM SỐ VÂN SÁNG, VÂN TỐI CÓ TRÊN MỘT MIỀN.
PHƯƠNG PHÁP GIẢI:
– Tính số vân sáng, vân tối trên đoạn MN bất kỳ (Phương pháp chặn k):
Để tìm số vân sáng, vân tối ta thay vị trí vân vào điều kiện:
+) $\frac{-MN}{2}\le \left[ \begin{array}{} {{x}_{s}}=ki \\ {} {{x}_{t}}=\left( k+0,5 \right)i \\ \end{array} \right.\le \frac{MN}{2}$ (nếu MN đối xứng qua vân trung tâm)
+) ${{x}_{N}}\le \left[ \begin{array}{} {{x}_{s}}=ki \\ {} {{x}_{t}}=\left( k+0,5 \right)i \\ \end{array} \right.\le {{x}_{M}}$ (nếu M, N bất kỳ)
M, N cùng phía với vân trung tâm thì ${{x}_{M}},{{x}_{N}}$ cùng dấu.
M, N khác phía với vân trung tâm thì ${{x}_{M}},{{x}_{N}}$ khác dấu.
Từ đó, ta suy ra được khoảng chạy của k, số giá trị k nguyên chính là số vân sáng hoặc vân tối cần tìm.
– Tính số vân sáng, vân tối trên trường giao thoa:
+) Trường giao thoa có chiều dài L là toàn bộ khu vực chứa các vân sáng, vân tối trên màn.
+) Dùng phương pháp chặn k ta có thể tìm được số vân sáng, vân tối trên L. Hoặc có thể sử dụng nhanh công thức: $\left\{ \begin{array}{} \\ {} \\ {} \\ \end{array} \right.$
Trong đó $\left[ \frac{L}{2i} \right]$ là phần nguyên của $\frac{L}{2i}$, ví dụ: $\left[ 2,3 \right]=2$.
VÍ DU MINH HỌA
|
Ví dụ 12: [Trích đề thi THPT QG năm 2010] Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng đơn sắc có bước sóng 0,6$\mu m$. Khoảng cách giữa hai khe là 1 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 2,5 m, bề rộng miền giao thoa là 1,25 cm. Tổng số vân sáng và vân tối có trong mỉền giao thoa là A. 19 vân. B. 17 vân. C. 15 vân. D. 21 vân. |
Lời giải:
$i=\frac{\lambda D}{a}=1,5\,\,\left( mm \right)\Rightarrow \left\{ \begin{array}{} {{N}_{s}}=2\left[ \frac{L}{2i} \right]+1=2\left[ \frac{12,5}{2.1,5} \right]+1=2\left[ 4,17 \right]+1=9 \\ {} {{N}_{t}}={{N}_{s}}-1=8 \\ \end{array} \right.$
$\Rightarrow {{N}_{t}}+{{N}_{s}}=17$vân. Chọn B.
|
Ví dụ 13: [Trích đề thi THPT QG năm 2010] Trong thí nghiệm Y-âng về giao thoa ánh sáng, các khe hẹp được chiếu sáng bởi ánh sáng đơn sắc. Khoảng vân trên màn là 1,2 mm. Trong khoảng giữa hai điểm M và N trên màn ở cùng một phía so với vân sáng trung tâm, cách vân trung tâm lần lượt 2 mm và 4,5 mm, quan sát được A. 2 vân sáng và 2 vân tối. B. 3 vân sáng và 2 vân tối. C. 2 vân sáng và 3 vân tối. D. 2 vân sáng và 1 vân tối. |
Lời giải:
Tại M: ${{k}_{M}}=\frac{2}{1,2}=1,7\,;$Tại N: ${{k}_{N}}=\frac{4,5}{1,2}=3,75.$
$\Rightarrow $Một điểm bất kỳ nằm trong đoạn MN sẽ có: $1,7\le k\le 3,75$
Nếu k nguyên thì cho vân sáng $\Rightarrow $Có 2 vân sáng ứng với k = 2, 3.
Nếu k bán nguyên thì cho vân tối $\Rightarrow $ Có 2 vân tối ứng với k = 2,5; 3,5. Chọn A.
|
Ví dụ 14: Trong thí nghiệm giao thoa Y-âng, trên màn quan sát hai vân sáng đi qua hai điểm M và P. Biết đoạn MP dài 7,2 mm đồng thời vuông góc với vân trung tâm và số vân sáng trên đoạn MP nằm trong khoảng từ 11 đến 15. Tại điểm N thuộc MP, cách M một đoạn 2,7 mm là vị trí của một vân tối. Số vân tối quan sát được trên MP là A. 11 vân. B. 12 vân. C. 13 vân. D. 14 vân. |
Lời giải:
Số vân sáng trên đoạn MP: $11<{{N}_{MP}}=\frac{MP}{i}+1<15\Rightarrow 0,514\,\,(mm)<i<0,72\,\,(mm)$
Vì M là vân sáng và N là vân tối nên: $MN=\left( n+0,5 \right)i$
$\Rightarrow 2,7=\left( n+0,5 \right)i\Rightarrow i=\frac{2,7}{n+0,5}\xrightarrow{0,514<i<0,72}3,25<n<4,75\Rightarrow n=4$
$\Rightarrow i=\frac{2,7}{4+0,5}=0,6$mm
Số vân tối trên đoạn MP: ${{N}_{t}}=\frac{MP}{i}=\frac{7,2}{0,6}=12$vân. Chọn B.
|
Ví dụ 15: Trong một thí nghiệm giao thoa ánh sáng với khe Y-âng, hai khe cách nhau 2 mm, khoảng cách từ hai khe tới màn quan sát là 2 m. Ánh sáng đơn sắc có bước sóng $\lambda $ = 0,5$\mu m$. Cho M và N là hai điểm nằm trong trường giao thoa, chúng nằm khác phía nhau so với vân chính giữa, có OM = 12,3 mm, ON = 5,2 mm. Số vân sáng và số vân tối trong đoạn MN là A. 35 vân sáng, 35 vân tối. B. 36 vân sáng, 36 vân tối. C. 35 vân sáng, 36 vân tối. D. 36 vân sáng, 35 vân tối. |
Lời giải:
Khoảng vân $i=\frac{\lambda D}{a}=0,5\,mm$
.
Vì hai điểm M và N trên màn ở khác phía so với vân sáng trung tâm nên có thể chọn
${{x}_{M}}=-12,3\,mm$và ${{x}_{N}}=5,2\,mm$
$\left\{ \begin{array}{} {{x}_{M}}\le ki=k.0,5\le {{x}_{N}}\Rightarrow -24,6\le k\le 10,4\Rightarrow k=\underbrace{-24;…;10}_{\text{c }\!\!\tilde{\mathrm{a}}\!\!\text{ 35 gi tr}} \\ {} {{x}_{M}}\le \left( m+0,5 \right)i=\left( m+0,5 \right)0,5\le {{x}_{N}}\Rightarrow -25,1\le m\le 9,9\Rightarrow m=\underbrace{-25;…;9}_{\text{c }\!\!\tilde{\mathrm{a}}\!\!\text{ 35 gi tr}} \\ \end{array} \right..$ Chọn A.
|
Ví dụ 16: Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng đơn sắc có Tiến hành thí nghiệm giao thoa ánh sáng với hai khe Y-âng với ánh sáng đơn sắc có với bước sóng ${{\lambda }_{1}}$ = 0,45$\mu m$, trong đoạn MN trên màn quan sát đối xứng qua vân sáng trung tâm người ta đếm được 13 vân sáng, trong đó M và N là hai vân sáng. Giữ nguyên điều kiện thí nghiệm và thay nguồn sáng bằng ánh sáng đơn sắc có bước sóng ${{\lambda }_{2}}$ = 0,60$\mu m$ thì số vân sáng trong đoạn MN trên màn quan sát là A. 12. B. 11. C. 10. D. 9. |
Lời giải:
MN đối xứng qua vân trung tâm, trong khoảng MN có 13 vân sáng nên tại M là vân sáng bậc 6, tại N là vân sáng bậc -6.
Tại M: ${{x}_{M}}=6{{i}_{1}}=n{{i}_{2}}\Leftrightarrow 6{{\lambda }_{1}}=n{{\lambda }_{2}}\Leftrightarrow 6.0,45=0,6.n\Rightarrow n=4,5$
$\Rightarrow $Số vân sáng trong đoạn MN thỏa mãn: $-4,5\le n\le 4,5$: có 9 giá trị n nguyên
$\Rightarrow $Có 9 vân sáng trong đoạn MN nếu sử dụng bước sóng ${{\lambda }_{2}}$. Chọn D.
DẠNG 3: BÀI TOÁN VỀ SỰ THAY ĐỔI KHOẢNG VÂN DO SỰ THAY ĐỔI KHOẢNG CÁCH HAY MÔI TRƯỜNG.
PHƯƠNG PHÁP GIẢI
– Khi thay đổi môi trường giao thoa bằng cách đặt hệ vào môi trường có chiết suất n thì bước sóng giảm n lần $\left( \lambda =\frac{{{\lambda }_{0}}}{n} \right)$ dẫn đến khoảng vân giảm n lần so với trong chân không $\left( {i}’=\frac{i}{n} \right)\Rightarrow $hệ vân thay đổi.
– Khi thay đổi bố trí thí nghiệm (thay đổi a và D) thì khoảng vân $\left( i=\frac{\lambda D}{a} \right)$ cũng thay đổi $\Rightarrow $hệ vân thay đổi. Thay đổi a và D thì có thể tại điểm M trên màn lúc đầu là vân sáng (tối) sẽ chuyển thành vân tối (sáng) có bậc cao hơn hoặc thấp hơn tùy thuộc a và D tăng hay giảm.
– Trong hai trường hợp này hệ vân thay đổi nhưng vân trung tâm không thay đổi vị trí.
VÍ DỤ MINH HỌA
|
Ví dụ 17: Tốc độ ánh sáng trong chân không là $c={{3.10}^{8}}m/s$. Cho ánh sáng đỏ bước sóng 0,72$\mu m$ trong chân không thì khi truyền từ chân không vào nước có chiết suất 4/3, tần số và bước sóng sẽ là A. $4,{{2.10}^{14}}\,Hz\,;\,\,0,72\,\mu m.$ B. $5,{{2.10}^{14}}\,Hz\,;\,\,0,54\,\mu m.$ C. $4,{{2.10}^{14}}\,Hz\,;\,\,0,54\,\mu m.$ D. $3,{{2.10}^{14}}\,Hz\,;\,\,0,76\,\mu m.$ |
Lời giải:
Tần số ánh sáng không đổi khi ánh sáng truyền giữa các môi trường:
$f=\frac{c}{{{\lambda }_{0}}}=\frac{{{3.10}^{8}}}{0,{{72.10}^{-6}}}=4,{{2.10}^{14}}\,Hz$
Bước sóng bị giảm đi n lần:
$v=\frac{c}{n}\Rightarrow \lambda =\frac{v}{f}=\frac{c}{nf}=\frac{{{\lambda }_{0}}}{n}=\frac{0,{{72.10}^{-6}}}{4/3}=5,{{4.10}^{-7}}m=0,54\,\mu m$. Chọn C.
|
Ví dụ 18: [Trích đề thi THPT QG năm 2012] Một ánh sáng đơn sắc màu cam có tần số f được truyền từ chân không vào một chất lỏng có chiết suất là 1,5 đối với ánh sáng này. Trong chất lỏng trên, ánh sáng này có A. màu cam và tần số 1,5f. B. màu tím và tần số 1,5f. C. màu cam và tần số f. D. màu tím và tần số f. |
Lời giải:
Tần số ánh sáng không đổi khi ánh sáng truyền giữa các môi trường do vậy ánh sáng vẫn có màu cam và tần số f. Chọn C.
|
Ví dụ 19: Thực hiện thí nghiệm giao thoa ánh sáng đơn sắc với khe Y-âng. Ban đầu thực hiện thí nghiệm trong không khí thu được vị trí vân sáng bậc 2 là ${{b}_{1}}$, khoảng vân giao thoa là ${{c}_{1}}$ và số vân sáng quan sát được trên màn quan sát là ${{n}_{1}}$. Giữ nguyên cấu trúc của hệ thống thí nghiệm. Thực hiện lại thí nghiệm trên trong môi trường nước thì thu được vị trí vân sáng bậc 2 là ${{b}_{2}}$, khoảng vân giao thoa là ${{c}_{2}}$ và số vân sáng quan sát được trên màn là ${{n}_{2}}$. Kết luận đúng là A. ${{b}_{1}}={{b}_{2}};\,\,{{c}_{1}}={{c}_{2}};\,\,{{n}_{1}}={{n}_{2}}.$ B. ${{b}_{1}}>{{b}_{2}};\,\,{{c}_{1}}>{{c}_{2}};\,\,{{n}_{1}}<{{n}_{2}}.$ C. ${{b}_{1}}<{{b}_{2}};\,\,{{c}_{1}}<{{c}_{2}};\,\,{{n}_{1}}<{{n}_{2}}.$ D. ${{b}_{1}}>{{b}_{2}};\,\,{{c}_{1}}<{{c}_{2}};\,\,{{n}_{1}}={{n}_{2}}.$ |
Lời giải:
Khoảng vân giao thoa khi thực hiện thí nghiệm trong môi trường không khí là i, thì khi thực hiện thí nghiệm này trong môi trường chiết suất n, khoảng vân sẽ là $\frac{i}{n}$(giảm đi n lần)
Do vậy ${{b}_{2}}<{{b}_{1}}$ và ${{c}_{2}}<{{c}_{1}}$
Khoảng vân giảm dẫn đến số vân quan sát được trên màn sẽ tăng ${{n}_{2}}>{{n}_{1}}$. Chọn B.
|
Ví dụ 20: Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng đơn sắc có bước sóng là 0,6$\mu m$. Khoảng cách giữa hai khe là 0,8 mm; khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 1,2 m. Màn quan sát rộng 15 mm đối xứng qua vân sáng trung tâm. Đặt hệ vào môi trường dầu trong suốt có chiết suất bằng 1,5. Hỏi số vân sáng quan sát được trên màn tăng lên thêm bao nhiêu vân so với lúc đặt trong chân không ? A. 4 vân. B. 8 vân. C. 5 vân. D. 7 vân. |
Lời giải:
- Trong chân không: $i=\frac{\lambda D}{a}=\frac{0,{{6.10}^{-6}}.1,2}{0,{{8.10}^{-3}}}=0,{{9.10}^{-3}}m=0,9\,mm$
Bề rộng vùng giao thoa $L=15\,mm\Rightarrow {{x}_{M}}=7,5\,mm;{{x}_{N}}=-7,5\,mm$
Số vân sáng trong miền MN thỏa mãn: ${{x}_{N}}\le {{x}_{s}}\le {{x}_{M}}$
$\Leftrightarrow -7,5\le {{x}_{s}}=n.0,9\le 7,5\Leftrightarrow -8,3\le n\le 8,3\Rightarrow $có 17 vân sáng.
- Trong môi trường dầu: ${\lambda }’=\frac{\lambda }{1,5}\Rightarrow {i}’=\frac{i}{1,5}=\frac{0,9}{1,5}=0,6\,mm$
Số vân sáng trong miền MN thỏa mãn: ${{x}_{N}}\le {{x}_{s}}\le {{x}_{M}}$
$\Leftrightarrow -7,5\le {{x}_{s}}=n.0,6\le 7,5\Leftrightarrow -12,5\le n\le 12,5\Rightarrow $có 25 vân sáng.
Khi nhúng vào dầu đã tăng lên 8 vân sáng so với trong chân không. Chọn B.
|
Ví dụ 21: Trong thí nghiệm Y-âng về giao thoa ánh sáng đơn sắc có bước sóng $\lambda $. Trên màn quan sát, tại điểm M có vân sáng bậc k. Lần lượt tăng rồi giảm khoảng cách giữa hai khe một đoạn $\Delta a$ sao cho vị trí vân trung tâm không thay đổi thì thấy M lần lượt có vân sáng bậc ${{k}_{1}}$ và ${{k}_{2}}$. Kết quả đúng là A. $2k={{k}_{1}}+{{k}_{2}}.$ B. $k={{k}_{1}}-{{k}_{2}}.$ C. $k={{k}_{1}}+{{k}_{2}}.$ D. $2k={{k}_{2}}-{{k}_{1}}.$ |
Lời giải:
Tại M là vị trí của vân sáng bậc k: ${{x}_{M}}=k\frac{D\lambda }{a}\Rightarrow a=\frac{kD\lambda }{{{x}_{M}}}\,\,\,\,\left( 1 \right)$
Thay đổi a một lượng $\Delta a$, ta có:
$\left\{ \begin{array}{} {{x}_{M}}={{k}_{1}}\frac{D\lambda }{a+\Delta a}\Rightarrow a+\Delta a=\frac{{{k}_{1}}D\lambda }{{{x}_{M}}}\,\,\, \\ {} {{x}_{M}}={{k}_{2}}\frac{D\lambda }{a-\Delta a}\Rightarrow a-\Delta a=\frac{{{k}_{2}}D\lambda }{{{x}_{M}}}\,\,\, \\ \end{array} \right.\Rightarrow 2a=\left( {{k}_{1}}+{{k}_{2}} \right)\frac{D\lambda }{{{x}_{M}}}\,\,\,\,\left( 2 \right)$
Từ (1) và (2), suy ra: $\Rightarrow 2k={{k}_{1}}+{{k}_{2}}.$ Chọn A.
|
Ví dụ 22: Trong thí nghiệm Y-âng, nguồn S phát bức xạ đơn sắc $\lambda $, màn quan sát cách mặt phẳng hai khe một khoảng không đổi D, khoảng cách giữa hai khe ${{S}_{1}}{{S}_{2}}=a$ có thể thay đổi (nhưng ${{S}_{1}}$ và ${{S}_{2}}$ luôn cách đều S). Xét điểm M trên màn, lúc đầu là vân sáng bậc 4, nếu lần lượt giảm hoặc tăng khoảng cách ${{S}_{1}}{{S}_{2}}$ một lượng $\Delta a$ thì tại đó là vân sáng bậc k và bậc 3k. Nếu tăng khoảng cách ${{S}_{1}}{{S}_{2}}$ thêm 2$\Delta a$ thì tại M là A. vân tối thứ 9. B. vâng sáng bậc 9. C. vân sáng bậc 7. D. vân sáng bậc 8. |
Lời giải:
$\left. \begin{array}{} {{x}_{M}}=k\frac{\lambda D}{a-\Delta a} \\ {} {{x}_{M}}=3k\frac{\lambda D}{a+\Delta a} \\ \end{array} \right\}\Rightarrow 1=3\frac{a-\Delta a}{a+\Delta a}\Rightarrow \Delta a=0,5a$
$\left. \begin{array}{} {{x}_{M}}=4\frac{\lambda D}{a} \\ {} {{x}_{M}}={k}’\frac{\lambda D}{a+2\Delta a} \\ \end{array} \right\}\Rightarrow 1=\frac{{{k}’}}{4.2}\Rightarrow {k}’=8.$ Chọn D.
|
Ví dụ 23: Trong thí nghiệm Y-âng về giao thoa với ánh sáng đơn sắc có bước sóng $\lambda $, khoảng cách giữa hai khe hẹp là a, khoảng cách từ mặt phẳng chứa hai khe hẹp đến màn quan sát là 2 m. Trên màn quan sát, tại điểm M cách vân sáng trung tâm 6 mm, có vân sáng bậc 5. Khi thay đổi khoảng cách giữa hai khe hẹp một đoạn bằng 0,2 mm sao cho vị trí vân sáng trung tâm không thay đổi thì tại M có vân sáng bậc 6. Giá trị của $\lambda $ bằng A. 0,60$\mu m$. B. 0,50$\mu m$. C. 0,45$\mu m$. D. 0,55$\mu m$. |
Lời giải:
Vì bậc vân tăng lên nên a tăng thêm: ${{x}_{M}}=5\frac{\lambda D}{a}=6\frac{\lambda D}{a+0,2}$
$\Rightarrow \frac{5}{a}=\frac{6}{a+0,2}\Rightarrow a=1\,\left( mm \right)\Rightarrow \lambda =\frac{a{{x}_{M}}}{5D}=0,{{6.10}^{-6}}\left( m \right)$. Chọn A.
|
Ví dụ 24: Trong thí nghiệm Y-âng về giao thoa với ánh sáng đơn sắc xác định, thì tại điểm M trên màn quan sát là vân sáng bậc 5. Sau đó giảm khoảng cách giữa hai khe một đoạn bằng 0,2 mm thì tại M trở thành vân tối thứ 5 so với vân sáng trung tâm. Ban đầu khoảng cách giữa hai khe là A. 2,2 mm. B. 1,2 mm. C. 2 mm. D. 1 mm. |
Lời giải:
${{x}_{M}}=5\frac{\lambda D}{a}=4,5\frac{\lambda D}{a-0,2}\Rightarrow \frac{5}{a}=\frac{4,5}{a-0,2}\Rightarrow a=2\,\left( mm \right)$. Chọn C.
|
Ví dụ 25: Trong thí nghiệm giao thoa Y-âng, khoảng cách hai khe là 1 mm. Giao thoa thực hiện với ánh sáng đơn sắc có bước sóng $\lambda $ thì tại điểm M có tọa độ 1,2 mm là vị trí vân sáng bậc 4. Nếu dịch màn xa thêm một đoạn 25 cm theo phương vuông góc với mặt phẳng hai khe thì tại M là vị trí vân sáng bậc 3. Xác định bước sóng. A. 0,4$\mu m$. B. 0,48$\mu m$. C. 0,45$\mu m$. D. 0,44$\mu m$. |
Lời giải:
Ta có $\left\{ \begin{array}{} {{x}_{M}}=4\frac{\lambda D}{a}\Rightarrow \frac{\lambda D}{a}=\frac{{{x}_{M}}}{4} \\ {} {{x}_{M}}=3\frac{\lambda \left( D+0,25 \right)}{a}=3\frac{\lambda D}{a}+0,75.\frac{\lambda }{a} \\ \end{array} \right.\Rightarrow \lambda =0,{{4.10}^{-6}}\left( m \right)$. Chọn A.
|
Ví dụ 26: Thực hiện thí nghiệm Y-âng về giao thoa với ánh sáng có bước sóng $\lambda $. Khoảng cách giữa hai khe hẹp là 1 mm. Trên màn quan sát, tại điểm M cách vân trung tâm 4,2 mm có vân sáng bậc 5. Giữ cố định các điều kiện khác, di chuyển dần màn quan sát dọc theo đường thẳng vuông góc với mặt phẳng chứa hai khe ra xa cho đến khi vân giao thoa tại M chuyển thành vân tối thứ hai thì khoảng dịch màn là 0,6 m. Bước sóng $\lambda $ bằng: A. 0,6$\mu m$. B. 0,5$\mu m$. C. 0,7$\mu m$. D. 0,4$\mu m$. |
Lời giải:
Vị trí điểm M: ${{x}_{M}}=5i=5\frac{\lambda D}{a}=4,{{2.10}^{-3}}\left( m \right)\,\,\,\,\left( 1 \right)$
Ban đầu, các vân tối tính từ vân trung tâm đến M lần lượt có tọa độ là 0,5i; 1,5i; 2,5i; 3,5i và 4,5i.
Khi dịch màn ra xa 0,6m M trở thành vân tối thứ 2 thì ${{x}_{M}}=3,5{i}’$ hay
${{x}_{M}}=3,5\frac{\lambda \left( D+0,6 \right)}{a}=4,{{2.10}^{-3}}\left( m \right)\,\,\,\,\left( 2 \right)$
Từ (1) và (2) tính ra: $D=1,4\,\,m,\,\,\lambda =0,6\,\,\mu m$. Chọn A.
|
Ví dụ 27: Trong thí nghiệm Y-âng, nguồn S phát bức xạ đơn sắc $\lambda $, màn quan sát cách mặt phẳng hai khe một khoảng không đổi D, khoảng cách giữa hai khe ${{S}_{1}}{{S}_{2}}$= a có thể thay đổi (nhưng ${{S}_{1}}$ và ${{S}_{2}}$ luôn cách đều S). Xét điểm M trên màn, lúc đầu là vân sáng bậc 4, nếu lần lượt giảm hoặc tăng khoảng cách ${{S}_{1}}{{S}_{2}}$ một lượng $\Delta a$ thì tại đó tương ứng là vân sáng bậc k hoặc 3k. Nếu tăng khoảng cách ${{S}_{1}}{{S}_{2}}$ thêm 2$\Delta a$ thì tại M là A. vân sáng bậc 8. B. vân tối thứ 9. C. vân sáng bậc 9. D. vân sáng thứ 7. |
Lời giải:
Ban đầu: ${{x}_{M}}=4\frac{\lambda D}{a}\,\,\,\left( 1 \right)$ Giảm $\Delta a$: ${{x}_{M}}=k\frac{\lambda D}{a-\Delta a}\,\,\,\,\,\,\,\left( 2 \right)$
Tăng $\Delta a$: ${{x}_{M}}=3k\frac{\lambda D}{a+\Delta a}\,\,\,\,\,\,\,\left( 3 \right)$ Tăng 2$\Delta a$: ${{x}_{M}}=n\frac{\lambda D}{a+2\Delta a}\,\,\,\,\,\,\,\left( 4 \right)$
Từ (2) và (3), được: $k\frac{\lambda D}{a-\Delta a}\,=3k\frac{\lambda D}{a+\Delta a}\,\Rightarrow a=2\Delta a\,\,\left( 5 \right)$
Từ (1) và (4), được: $n\frac{\lambda D}{a+2\Delta a}=4\frac{\lambda D}{a}\Leftrightarrow \frac{a+2\Delta a}{n}=\frac{a}{4}\,\,\,\left( 6 \right)$
Thay (5) vào (6), được: $\frac{2\Delta a+2\Delta a}{n}=\frac{2\Delta a}{4}\,\Rightarrow n=8$. Chọn A.
|
Ví dụ 28: Thí nghiệm giao thoa Y-âng với ánh sáng đơn sắc có bước sóng $\lambda $ = 0,6$\mu m$, khoảng cách giữa hai khe a = l mm, khoảng cách hai khe đến màn D = 2 m. Màn ảnh giao thoa có khối lượng 100g gắn với một lò xo nằm ngang có độ cứng là k, sao cho màn có thể dao động điều hòa theo phương ngang trùng với trục của lò xo và vuông góc với mặt phẳng hai khe (xem hình vẽ). Tại thời điểm t = 0, truyền cho màn từ vị trí cân bằng một vận tốc ban đầu hướng về phía hai khe để màn dao động điều hòa với biên độ 40 cm. Thời gian từ lúc màn bắt đầu dao động đến khi điểm M trên màn cách vân trung tâm một đoạn b = 8 mm cho vân sáng lần thứ 4 là 0,29s. Độ cứng k có giá trị gần nhất là A. 10 N/m. B. 25 N/m. C. 20 N/m. D. 15 N/m. |
Lời giải:
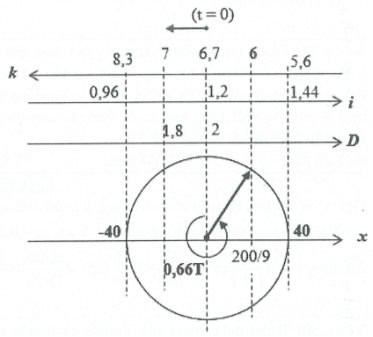
Ta có: $\frac{\lambda \left( D-A \right)}{a}\le i\le \frac{\lambda \left( D+A \right)}{a}$
$\Leftrightarrow 0,96\le i\le 1,44\Rightarrow 5,6\le k\le 8,3$
+) Ban đầu t = 0: $i=1,2mm\Rightarrow {{k}_{M}}=6,7$
$\Rightarrow $Lần thứ 4 tại M cho vân sáng ứng với k
= 6 (lần 2). [do truyền cho màn E dịch
chuyển về phía 2 khe nên D giảm $\Rightarrow $ i giảm
$\Rightarrow $ k tăng: 6,7 $\to $ 7 (sáng lần 1) $\to $ 8,3 $\to $ 7
(sáng lần 2) $\to $ 6,7 $\to $ 6 (sáng lần 3) $\to $ 5,6
$\to $ 6 (sáng lần 4)].
$\Rightarrow i=\frac{8}{6}=\frac{4}{3}mm\Rightarrow D=20/9\,m$
$\Rightarrow x=\frac{2}{9}m=\frac{200}{9}cm.$
$\Rightarrow 0,66T=0,29s\Rightarrow T=0,44s$
$\Rightarrow k\approx 20,4\,N/m$. Chọn C.
DẠNG 4: DỊCH CHUYỂN KHE SÁNG, ĐẶT THÊM BẢN MỎNG.
a) Dịch chuyển khe S.
PHƯƠNG PHÁP GIẢI
Gọi y là độ dịch chuyển của nguồn sáng S. Hiệu đường đi của hai sóng kết hợp tại M:
$\Delta d=\left( {{d}_{2}}^{\prime }+{{d}_{2}} \right)-\left( {{d}_{1}}^{\prime }+{{d}_{1}} \right)=\left( {{d}_{2}}^{\prime }-{{d}_{1}}^{\prime } \right)+\left( {{d}_{2}}-{{d}_{1}} \right)=\frac{ay}{d}+\frac{ax}{D}$
– Tại M là vân sáng nếu $\Delta d=k\lambda $, là vân tối nếu $\Delta d=\left( m-0,5 \right)\lambda $:
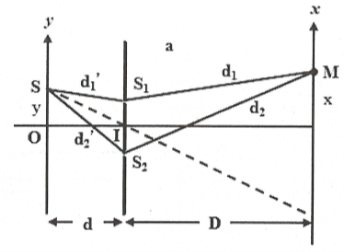
$\Rightarrow \left\{ \begin{array}{} \\ {} \\ {} \\ {} \\ \end{array} \right.$
– Vị trí vân sáng trung tâm (k = 0):
$\frac{ay}{d}+\frac{a{{x}_{0}}}{D}=0.\lambda \Rightarrow {{x}_{0}}=-\frac{Dy}{d}$
Như vậy:
+) Nếu dịch chuyển nguồn S theo phương
song song với ${{S}_{1}}{{S}_{2}}$ một khoảng y thì vân trung tâm
cũng như hệ thống vân trên màn dịch chuyển theo
chiều ngược lại một đoạn $\left| {{x}_{0}} \right|=\left| \frac{Dy}{d} \right|$, sao cho S, I và vị trí vân trung tâm luôn thẳng hàng.
+) Vị trí vân sáng bậc k: $x={{x}_{0}}\pm ki$.
+) Vị trí vân tối thứ k: $x={{x}_{0}}\pm \left( k-0,5 \right)i$.
VÍ DỤ MINH HỌA
|
Ví dụ 29: Trong thí nghiệm Y-âng về giao thoa ánh sáng. Khe hẹp S phát ra ánh sáng đơn sắc có bước sóng $\lambda $ = 0,64$\mu m$; khoảng cách từ S đến màn chứa hai khe ${{S}_{1}}$ và ${{S}_{2}}$ là 60 cm; biết ${{S}_{1}}{{S}_{2}}$ = a = 0,3 mm, khoảng cách từ ${{S}_{1}}$ và ${{S}_{2}}$ đến màn quan sát là D = 1,5 m. Nguồn sáng Đ phải dịch chuyển một đoạn ngắn nhất bằng bao nhiêu theo phương song song với màn quan sát để trên màn vị trí vân sáng bậc 2 trở thành vân tối thứ 2 ? A. 1,28 mm. B. 0,064 mm. C. 0,64 mm. D. 0,40 mm. |
Lời giải:
Gọi ${{x}_{0}}$ là độ dịch chuyển của vân sáng, y là độ dịch chuyển của nguồn sáng.
$\Rightarrow $Vân tối sáng bậc 2 thành vân tối bậc 2$\Rightarrow {{x}_{0}}=0,5i.$
Áp dụng $\left| {{x}_{0}} \right|=\left| \frac{Dy}{d} \right|\Rightarrow y=\frac{d\left| {{x}_{0}} \right|}{D}=\frac{d}{D}.0,5i=\frac{d}{D}\frac{D\lambda }{2a}=\frac{0,6}{1,2}\frac{1,5.0,{{64.10}^{-6}}}{2.0,{{3.10}^{-3}}}=0,64\,mm$. Chọn C.
|
Ví dụ 30: Trong thí nghiệm của Young, cách giữa hai khe ${{S}_{1}}{{S}_{2}}$ là 1,2 mm. Nguồn S phát ra ánh sáng đơn sắc đặt cách mặt phẳng hai khe một khoảng d và phát ánh sáng đơn sắc có bước sóng 0,5$\mu m$. Nếu dời S theo phương song song với ${{S}_{1}}{{S}_{2}}$ một đoạn 2 mm thì hệ vân dịch chuyển một đoạn bằng 15 khoảng vân. Giá trị d là A. 0,32 m. B. 0,26 m. C. 3,2 m. D. 2,6 m. |
Lời giải:
Gọi ${{x}_{0}}=15i$ là độ dịch chuyển của vân, y = 2 mm là độ dịch chuyển của nguồn.
Áp dụng$\left| {{x}_{0}} \right|=\left| \frac{Dy}{d} \right|=15i\Leftrightarrow 15\frac{\lambda D}{a}=\frac{D.y}{d}$
$\Rightarrow d=\frac{y.a}{15\lambda }=\frac{{{2.10}^{-3}}.1,{{2.10}^{-3}}}{15.0,{{5.10}^{-6}}}=0,32\,m$. Chọn A.
|
Ví dụ 31: Trong thí nghiệm giao thoa Y-âng với ánh sáng đơn sắc, khoảng cách hai khe đến màn là D thì khoảng vân giao thoa là 2 mm. Khoảng cách từ khe S đến mặt phẳng hai khe là d = 0,25.D. Cho khe S dịch chuyển theo phương song song với màn theo chiều dương một đoạn 2 mm thì vân sáng bậc 2 nằm ở toạ độ nào trong số các toạ độ sau? A. -5 mm. B. +4 mm. C. +8 mm. D. -12 mm. |
Lời giải:
Gọi ${{x}_{0}}$ là độ dịch chuyển của vân, y là độ dịch chuyển của nguồn.
Áp dụng $\left| {{x}_{0}} \right|=\left| \frac{Dy}{d} \right|=\frac{D}{0,25d}.2=8mm$, khe S dịch chuyển theo chiều dương lên trên thì hệ vân sẽ dịch chuyển theo chiều âm xuống dưới $\Rightarrow {{x}_{0}}=-8\,mm$.
Tọa độ vân sáng bậc 2: $x={{x}_{0}}\pm 2i=-8\pm 2.2\Rightarrow x=-4\,mm$ hoặc $x=-12\,mm$. Chọn D.
|
Ví dụ 32: Trong thí nghiệm giao thoa Y-âng khoảng cách hai khe 0,6 mm. Khoảng cách từ mặt phẳng hai khe đến màn 2 m. Khoảng cách từ khe S đến mặt phẳng hai khe 80 cm. Giao thoa thực hiện với ánh sáng đơn sắc có bước sóng 0,6$\mu m$. Cho khe S dịch chuyển theo phương song song với màn một đoạn tối thiểu bằng bao nhiêu và theo chiều nào để tại vị trí trên màn có toạ độ x = -1,3 mm chuyển thành vân tối. A. 0,52 mm theo chiều âm. B. 0,12 mm theo chiều âm. C. 0,12 mm theo chiều dương. D. 0,52 mm theo chiều dương. |
Lời giải:
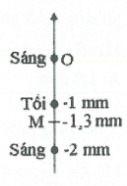
Khoảng vân $i=\frac{\lambda D}{a}=2\,\left( mm \right)$
Vân tối nằm gần M nhất là vân nằm phía trên M và cách M là ${{x}_{\min }}=0,3$mm. Ta
phải dịch vân tối này xuống $\Rightarrow $khe S phải dịch lên một đoạn y (dịch theo chiều
dương) sao cho: ${{x}_{0}}=y\frac{D}{d}={{x}_{\min }}$
$\Leftrightarrow y\frac{2}{0,8}=0,3\Rightarrow y=0,12\,mm$. Chọn C.
|
Ví dụ 33: Thực hiện giao thoa ánh sáng với khe Y-âng. Nguồn sáng đơn sắc có bước sóng 500 nm, khoảng cách hai khe a = l mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát D = 2 m, khoảng cách từ khe F đến mặt phẳng chứa hai khe là d = 1 m. Cho khe F dao động điều hòa trên trục Ox vuông góc với trục đối xứng của hệ quanh vị trí O cách đầu hai khe ${{F}_{1}},{{F}_{2}}$ với phương trình $x=cos\left( 2\pi t-\pi /2 \right)$ (mm). Trên màn, xét điểm M cách vân trung tâm một khoảng 1 mm. Tính cả thời điểm t = 0, điểm M trùng với vân sáng lần thứ 2018 vào thời điểm A. 252 s. B. 504 + 1/2 s. C. 252 + 1/6 s. D. 252 + 1/12 s. |
Lời giải:
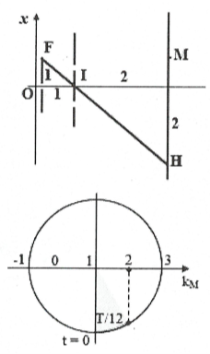
Khe F dao động điều hòa thì vị trí vân trung tâm H cũng dao động
điều hòa theo phương thẳng đứng. Khi khe F đi lên thì H đi xuống và
ngược lạì, sao cho F, I, H luôn thẳng hàng. Ta có:
${{x}_{F}}=cos\left( 2\pi t-\frac{\pi }{2} \right)\left( mm \right)\Rightarrow {{x}_{H}}=2cos\left( 2\pi t+\frac{\pi }{2} \right)\left( mm \right)$
Khoảng vân $i=\frac{\lambda D}{a}=1\,mm.$
$\Rightarrow {{k}_{M}}=\frac{MH}{i}=\frac{{{x}_{M}}-{{x}_{H}}}{1}=1-2cos\left( 2\pi t+\frac{\pi }{2} \right)=1+2cos\left( 2\pi t-\frac{\pi }{2} \right)\,mm.$
Do hàm cos chạy từ $-1\to 1$ nên ${{k}_{M}}$ chạy từ $-1\to 3$ $\Rightarrow $Trong 1T, M
trùng với 8 vân sáng.
Tách 2018 vân sáng = 252.8 + 1 (tính lần đầu tiên t = 0 $\Rightarrow {{k}_{M}}=1$
nữa là 2018 lần) $\Rightarrow t=252T+\Delta t$
$\Rightarrow \Delta t=\frac{T}{12}\Rightarrow t=252T+\frac{T}{12}=252.1+\frac{1}{12}s$. Chọn D.
|
Ví dụ 34: Trong thí nghiệm giao thoa ánh sáng Y-âng, khoảng cách từ mặt phẳng hai khe đến màn D = 2 m, nguồn sáng S (cách đều hai khe) cách mặt phẳng hai khe một khoảng d = 1,0 m phát ánh sáng đơn sắc có bước sóng $\lambda $ = 0,75$\mu m$. Bố trí thí nghiệm sao cho vị trí của nguồn sáng S có thể thay đổi nhưng luôn song song với ${{S}_{1}}{{S}_{2}}$. Lúc đầu trên màn thu được tại O là vân sáng trung tâm và khoảng cách giữa 5 vân sáng liên tiếp là 3 mm. Sau đó cố định vị trí khe ${{S}_{1}}$ tịnh tiến khe ${{S}_{2}}$ lại gần khe ${{S}_{1}}$ một đoạn $\Delta a$ sao cho tại O là vân sáng. Giá trị nhỏ nhất của $\Delta a$ là A. 1,0 mm. B. 2,5 mm. C. 1,8 mm. D. 0,5 mm. |
Lời giải:
5 vân sáng ứng với 4 khoảng vân: $4i=3\Rightarrow i=0,75\,mm$
Mà $i=\frac{\lambda D}{a}\Rightarrow a=\frac{\lambda D}{i}=\frac{0,{{75.10}^{-6}}.2}{0,{{75.10}^{-3}}}=2\,mm$
Nguồn sáng S, trung điểm M của ${{S}_{1}}{{S}_{2}}$, vân trung tâm trên màn luôn thẳng hàng.
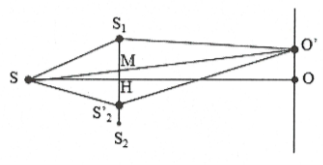
Do đó, khi ${{S}_{2}}$dịch chuyển lại gần ${{S}_{1}}$ thì vân trung tâm ${O}’$ dịch chuyển lên trên.
Áp dụng định lý Talét trong tam giác: $\frac{MH}{{O}’O}=\frac{d}{D+d}=\frac{1}{2+1}\Rightarrow O{O}’=3MH\,\,\left( * \right)$
Trong đó: $MH=\Delta a/2$
Để O là vân sáng thì $O{O}’$= khoảng vân mới $=\frac{\lambda D}{a-\Delta a}$
Thay vào (*): $\frac{\lambda D}{a-\Delta a}=1,5\Delta a\Leftrightarrow 1,5=1,5\left( 2-\Delta a \right).\Delta a\Rightarrow \Delta a=1\,mm$. Chọn A.
b) Đặt thêm bản mỏng.
PHƯƠNG PHÁP GIẢI
– Trên đường đi của nguồn ${{S}_{1}}$ đặt bản mỏng có độ dày e
chiết suất n, thì đường đi của tia sáng qua bản mỏng “dài”
hơn so với khi không có bản mỏng là $e\left( n-1 \right)$. Nên hiệu
quang trình lúc đó là ${{d}_{2}}-{{d}_{1}}=\frac{ax}{D}-e\left( n-1 \right)$, hiện tượng
giao thoa vẫn xảy ra, khoảng vân không thay đổi nhưng vân
trung tâm dịch một đoạn trên màn $\Delta x=\frac{\left( n-1 \right)eD}{a}$ về phía
có bản mỏng.
+) Đặt hai bản như nhau trên đường truyền của ${{S}_{1}},{{S}_{2}}$ thì hệ vân không dịch chuyển.
+) Đặt hai bản khác nhau, độ dịch chuyển sẽ là $\left| {{x}_{1}}-{{x}_{2}} \right|$.
– Đặt bản thủy tinh sau ${{S}_{1}}$ thì hệ vân dịch về phía ${{S}_{1}}$ một đoạn $\Delta x=\frac{\left( n-1 \right)eD}{a}$. Dịch S theo phương song song với ${{S}_{1}}{{S}_{2}}$ về phía ${{S}_{1}}$ thì hệ vân dịch chuyển về ${{S}_{2}}$ một đoạn ${{x}_{0}}=y\frac{D}{d}$. Để cho hệ vân trở về vị trí ban đầu thì ${{x}_{0}}=\Delta x$.
VÍ DỤ MINH HỌA
|
Ví dụ 35: Trong thí nghiệm giao thoa Y-âng với ánh sáng đơn sắc, khoảng cách giữa hai khe 1 mm, khoảng cách hai khe đến màn 1 m. Người ta đặt một bản thủy tinh có bề dày 10$\mu m$ có chiết suất 1,5 trước khe ${{S}_{1}}$. Hỏi hệ thống vân giao thoa trên màn sẽ dịch A. về phía ${{S}_{1}}$ là 3 mm. B. về phía ${{S}_{2}}$ là 5 mm. C. về phía ${{S}_{1}}$ là 5 mm. D. về phía ${{S}_{2}}$ là 3 mm. |
Lời giải:
Đặt bản mỏng trước ${{S}_{1}}$ nên hệ vân dịch về phía ${{S}_{1}}$ một đoạn:
$\Rightarrow \Delta x=\frac{\left( n-1 \right)eD}{a}=\frac{\left( 1,5-1 \right){{.10.10}^{-6}}.1}{{{10}^{-3}}}={{5.10}^{-3}}\,m=5\,mm$. Chọn C.
|
Ví dụ 35: Trong thí nghiệm giao thoa Y-âng, khoảng cách giữa hai khe 1,5 mm, khoảng cách hai khe đến màn 3 m. Giao thoa thực hiện với ánh sáng đơn sắc 0,56$\mu m$. Người ta đặt một bản thủy tinh có bề dày 1 $\mu m$ có chiết suất 1,5 trước khe ${{S}_{2}}$. Vị trí nào sau đây là vị trí vân sáng bậc 5. A. x = 7,0 mm. B. x = 4,6 mm. C. x = 5,1 mm. D. x = 2,4 mm. |
Lời giải:
Khoảng vân $i=\frac{\lambda D}{a}=1,22\,mm$
Vị trí vân trung tâm: ${{x}_{0}}=-\frac{\left( n-1 \right)eD}{a}=-\frac{\left( 1,5-1 \right){{.1.10}^{-6}}.3}{1,{{5.10}^{-3}}}=-1\,\,mm$
Vị trí vân sáng bậc 5: $x={{x}_{0}}\pm 5i=-1\pm 5.1,22=\left[ \begin{array}{} 5,1\,mm \\ {} -7,1\,mm \\ \end{array} \right.$. Chọn C.
|
Ví dụ 36: Trong thí nghiệm giao thoa Y-âng, khoảng cách giữa hai khe 0,75 mm, khoảng cách hai khe đến màn 3 m. Giao thoa thực hiện với ánh sáng đơn sắc 0,5$\mu m$. Hỏi phải đặt một bản thủy tinh có chiết suất 1,5 có bề dày nhỏ nhất bao nhiêu và đặt ở ${{S}_{1}}$ hay ${{S}_{2}}$ thì tại vị trí x = +0,8 mm (chiều dương cùng chiều với chiều từ ${{S}_{2}}$ đến ${{S}_{1}}$) trở thành vị trí của vân sáng? A. Đặt ${{S}_{1}}$ dày 0,4$\mu m$. B. Đặt ${{S}_{2}}$ dày 0,4$\mu m$. C. Đặt ${{S}_{1}}$ dày 1,5$\mu m$. D. Đặt ${{S}_{2}}$ dày 1,5$\mu m$. |
Lời giải:
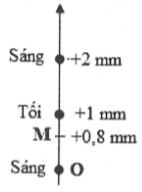
Khoảng vân $i=\frac{\lambda D}{a}=2\,mm$
Vân sáng nằm gần M nhất là vân nằm phía dưới M và cách M là
${{x}_{\min }}=0,8\,mm$. Ta phải dịch vân sáng này lên, bản thủy tinh phải đặt ở khe
${{S}_{1}}$ sao cho: $\Delta x=\frac{\left( n-1 \right)eD}{a}={{x}_{\min }}$
$\Rightarrow \frac{\left( 1,5-1 \right)eD}{0,{{75.10}^{-3}}}=0,{{8.10}^{-3}}\Rightarrow e=0,{{4.10}^{-6}}\,m$. Chọn A.
|
Ví dụ 37: Một khe hẹp S phát ra ánh sáng đơn sắc chiếu sáng hai khe ${{S}_{1}}$ và ${{S}_{2}}$ song song, cách đều S và cách nhau một khoảng 0,6 mm. Khoảng cách từ mặt phẳng hai khe đến S là 0,5 m. Chắn khe ${{S}_{2}}$ bằng một bản mỏng thủy tinh có độ dày 0,005 mm chiết suất 1,6. Khe S phải dịch chuyển theo chiều nào và bằng bao nhiêu để đưa hệ vân trở lại vị trí ban đầu như khi chưa đặt bản mỏng A. Khe S dịch về ${{S}_{1}}$ một đoạn 2,2 cm. B. Khe S dịch về ${{S}_{1}}$ một đoạn 2,5 mm. C. Khe S dịch về ${{S}_{2}}$ một đoạn 2,5 mm. D. Khe S dịch về ${{S}_{2}}$ một đoạn 2,2 mm. |
Lời giải:
Đặt bản thủy tinh sau ${{S}_{2}}$ thì hệ vân dịch về phía ${{S}_{2}}$ một đoạn $\Delta x=\frac{\left( n-1 \right)eD}{a}$. Dịch S theo phương song song với ${{S}_{1}}{{S}_{2}}$ về phía ${{S}_{2}}$ thì hệ vân dịch chuyển về ${{S}_{1}}$ một đoạn ${{x}_{0}}=y\frac{D}{d}$. Để cho hệ vân trở về vị trí ban đầu thì ${{x}_{0}}=\Delta x$ hay $y\frac{D}{d}=\frac{\left( n-1 \right)eD}{a}$
$\Rightarrow y=\frac{\left( n-1 \right)ed}{a}=\frac{\left( 1,6-1 \right).0,{{005.10}^{-3}}.0,5}{0,{{6.10}^{-3}}}=0,0025\,m=2,5\,mm$. Chọn C.