BÀI TẬP VỀ ĐIỆN XOAY CHIỀU CÓ 2 PHẦN TỬ CÓ ĐÁP ÁN CHI TIẾT
| Bài tập 1: [Trích đề thi Đại học năm 2008] Cho đoạn mạch gồm điện trở thuần R nối tiếp tụ điện có điện dung C. Khi dòng điện xoay chiều có tần số góc $\text{ }\!\!\omega\!\!\text{ }$ chạy qua thì tổng trở của đoạn mạch là
A. $\sqrt{{{\text{R}}^{\text{2}}}\text{+}{{\left( \frac{\text{1}}{\text{ }\!\!\omega\!\!\text{ C}} \right)}^{\text{2}}}}$. B. $\sqrt{{{\text{R}}^{\text{2}}}-{{\left( \frac{\text{1}}{\text{ }\!\!\omega\!\!\text{ C}} \right)}^{\text{2}}}}$. C. $\sqrt{{{\text{R}}^{\text{2}}}\text{+}{{\left( \text{ }\!\!\omega\!\!\text{ C} \right)}^{\text{2}}}}$. D. $\sqrt{{{\text{R}}^{\text{2}}}-{{\left( \text{ }\!\!\omega\!\!\text{ C} \right)}^{\text{2}}}}.$ |
HD giải: Tổng trở của mạch: $\text{Z=}\sqrt{{{\text{R}}^{\text{2}}}\text{+Z}_{\text{C}}^{\text{2}}}=\sqrt{{{\text{R}}^{\text{2}}}\text{+}{{\left( \frac{\text{1}}{\text{ }\!\!\omega\!\!\text{ C}} \right)}^{\text{2}}}}.$ Chọn A.
| Bài tập 2: Một đoạn mạch điện gồm điện trở $\text{R = 50 }\!\!\Omega\!\!\text{ }$mắc nối tiếp với cuộn thuần cảm có $\text{L=}\frac{\text{0,5}}{\text{ }\!\!\pi\!\!\text{ }}\left( \text{H} \right)$. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều $\text{u}=100\sqrt{2}\text{cos}\left( \text{100 }\!\!\pi\!\!\text{ t}-\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)\left( \text{V} \right)\text{.}$ Biểu thức của cường độ dòng điện qua đoạn mạch là:
A. $\text{i}=2\text{cos}\left( \text{100 }\!\!\pi\!\!\text{ t}-\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right)\left( \text{A} \right)\text{.}$ B. $\text{i}=2\sqrt{2}\text{cos}\left( \text{100 }\!\!\pi\!\!\text{ t}-\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)\left( \text{A} \right)\text{.}$ C. $\text{i}=2\sqrt{2}\text{cos}\left( \text{100 }\!\!\pi\!\!\text{ t} \right)\left( \text{A} \right)\text{.}$ D. $\text{i}=2\text{cos}\left( \text{100 }\!\!\pi\!\!\text{ t} \right)\left( \text{A} \right)\text{.}$ |
HD giải: Ta có ${{\text{Z}}_{\text{L}}}\text{= L }\!\!\omega\!\!\text{ = 50 }\!\!\Omega\!\!\text{ }$.
Mạch gồm điện trở thuần và cuộn thuần cảm.
Do đó ${{\text{Z}}_{\text{RL}}}\text{=}\sqrt{{{\text{R}}^{\text{2}}}\text{+Z}_{\text{L}}^{\text{2}}}\text{ = 50}\sqrt{\text{2}}\Rightarrow {{\text{I}}_{\text{0}}}\text{=}\frac{{{\text{U}}_{\text{0}}}}{\text{Z}}\text{=2A}\text{.}$
Lại có: $\tan \text{ }\!\!\varphi\!\!\text{ =}\frac{{{\text{Z}}_{\text{L}}}}{\text{R}}\text{=1}\Rightarrow \text{ }\!\!\varphi\!\!\text{ =}{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{u}}}-{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{i}}}=\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\Rightarrow {{\text{ }\!\!\varphi\!\!\text{ }}_{\text{i}}}=-\frac{\text{ }\!\!\pi\!\!\text{ }}{2}$
Vậy $\text{i}=2\text{cos}\left( \text{100 }\!\!\pi\!\!\text{ t}-\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right)\left( \text{A} \right)\text{.}$ Chọn A.
| Bài tập 3: [Trích đề thi Cao đẳng năm 2009] Khi đặt hiệu đến thế không đổi 30V vào hai đầu đoạn mạch gồm điện trở thuần mắc nối tiếp với cuộn cảm thuần có độ tự cảm $\frac{1}{\text{4 }\!\!\pi\!\!\text{ }}\left( \text{H} \right)$ thì dòng điện trong đoạn mạch là dòng điện một chiều có cường độ 1 A. Nếu đặt vào hai đầu đoạn mạch này điện áp $\text{u}=150\sqrt{2}\text{cos120 }\!\!\pi\!\!\text{ t}\left( \text{V} \right)$ thì biểu thức của cường độ dòng điện trong đoạn mạch là:
A. $\text{i}=5\sqrt{2}\text{cos}\left( \text{120 }\!\!\pi\!\!\text{ t+}\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)\left( \text{A} \right)\text{.}$ B. $\text{i}=5\sqrt{2}\text{cos}\left( \text{120 }\!\!\pi\!\!\text{ t}-\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)\left( \text{A} \right)\text{.}$ C. $\text{i}=5\text{cos}\left( \text{120 }\!\!\pi\!\!\text{ t+}\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)\left( \text{A} \right)\text{.}$ D. $\text{i}=5\text{cos}\left( \text{120 }\!\!\pi\!\!\text{ t}-\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)\left( \text{A} \right)$ |
HD giải: Ta có: ${{\text{Z}}_{\text{L}}}\text{= L }\!\!\omega\!\!\text{ = 30 }\!\!\Omega\!\!\text{ }$.
Ban đầu dòng điện là dòng một chiều do đó ta coi nó chỉ có điện trở R.
Suy ra $\text{R=}\frac{\text{U}}{\text{I}}\text{= 30 }\!\!\Omega\!\!\text{ }\text{.}$Khi đó $\tan \text{ }\!\!\varphi\!\!\text{ =}\frac{{{\text{Z}}_{\text{L}}}}{\text{R}}\text{=1}\Rightarrow {{\text{ }\!\!\varphi\!\!\text{ }}_{\text{u}}}-{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{i}}}=\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\Rightarrow {{\text{ }\!\!\varphi\!\!\text{ }}_{\text{i}}}=0-\frac{\text{ }\!\!\pi\!\!\text{ }}{4}=-\frac{\text{ }\!\!\pi\!\!\text{ }}{4}.$
Mặt khác $\text{Z=}\sqrt{{{\text{R}}^{\text{2}}}\text{+Z}_{\text{L}}^{\text{2}}}\text{ = 30}\sqrt{\text{2}}\Rightarrow {{\text{I}}_{\text{0}}}\text{=}\frac{{{\text{U}}_{\text{0}}}}{\text{Z}}\text{=}\frac{150\sqrt{2}}{30\sqrt{2}}\text{=5A}\text{.}$
Do đó $\text{i}=5\text{cos}\left( \text{120 }\!\!\pi\!\!\text{ t}-\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)\left( \text{A} \right)\text{.}$ Chọn D.
| Bài tập 4: [Trích đề thi Cao đẳng năm 2012] Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở thuần mắc nối tiếp với tụ điện. Biết điện áp hiệu dụng giữa hai đầu điện trở và giữa hai bản tụ điện lần lượt là 100V và $\text{100}\sqrt{\text{3}}$V. Độ lệch pha giữa điện áp hai đầu đoạn mạch và điện áp giữa hai bản tụ điện có độ lớn bằng:
A. $\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}$ B. $\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}$. C.. $\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{8}}$. D. $\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}$. |
HD giải: Mạch điện gồm điện trở thuần và tụ điện
Ta có: $\text{tan }\!\!\varphi\!\!\text{ =}-\frac{{{\text{U}}_{\text{C}}}}{{{\text{U}}_{\text{R}}}}\text{=}–\sqrt{\text{3}}\Rightarrow \text{ }\!\!\varphi\!\!\text{ =}-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}\text{.}$
Khi đó $\left( \widehat{\overrightarrow{\text{U}}\text{;}\overrightarrow{\text{I}}} \right)=60{}^\circ \Rightarrow \left( \widehat{\overrightarrow{{{\text{U}}_{\text{C}}}}\text{;}\overrightarrow{\text{U}}} \right)=30{}^\circ $. Chọn A.
| Bài tập 5: [Trích đề thi Cao đẳng năm 2012] Đặt điện áp $\text{u=}{{\text{U}}_{\text{0}}}\text{cos}\left( \text{ }\!\!\omega\!\!\text{ t}-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}} \right)$ vào hai đầu đoạn mạch gồm điện trở thuần R mắc nối tiếp với cuộn cảm thuần có độ tự cảm L, cường độ dòng điện trong mạch là $\text{i=}{{\text{I}}_{\text{0}}}\text{cos}\left( \text{ }\!\!\omega\!\!\text{ t}-\frac{\text{2 }\!\!\pi\!\!\text{ }}{\text{3}} \right)$. Biết ${{\text{U}}_{\text{0}}}$, ${{\text{I}}_{\text{0}}}$và $\text{ }\!\!\omega\!\!\text{ }$ không đổi. Hệ thức đúng là:
A. $\text{R=3 }\!\!\omega\!\!\text{ L}\text{.}$ B. $\text{ }\!\!\omega\!\!\text{ L=3R}\text{. }$ C. $\text{R=}\sqrt{\text{3}}\text{ }\!\!\omega\!\!\text{ L}$ D. $\text{ }\!\!\omega\!\!\text{ L=}\sqrt{\text{3}}\text{R}\text{.}$ |
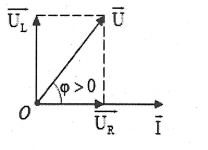
| HD giải: Mạch điện gồm điện trở và tụ điện.
Ta có: $\text{tan }\!\!\varphi\!\!\text{ =}\frac{{{\text{U}}_{\text{L}}}}{{{\text{U}}_{\text{R}}}}\text{=}\frac{{{\text{Z}}_{\text{L}}}}{\text{R}}$ Trong đó $\text{ }\!\!\varphi\!\!\text{ = }{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{u}}}-{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{i}}}=-\frac{\text{ }\!\!\pi\!\!\text{ }}{2}+\frac{\text{2 }\!\!\pi\!\!\text{ }}{3}=\frac{\text{ }\!\!\pi\!\!\text{ }}{6}.$ Suy ra $\tan \frac{\text{ }\!\!\pi\!\!\text{ }}{6}=\frac{\text{L }\!\!\omega\!\!\text{ }}{\text{R}}\Rightarrow \text{R=}\sqrt{\text{3}}\text{ }\!\!\omega\!\!\text{ L}\text{. }$Chọn C.
|
 |
| Bài tập 6: [Trích đề thi Cao đẳng năm 2010] Đặt điện áp $\text{u=}{{\text{U}}_{\text{0}}}\text{cos }\!\!\omega\!\!\text{ t}\left( \text{V} \right)$vào hai đầu đoạn mạch gồm điện trở thuần R và tụ điện C mắc nối tiếp. Biết điện áp giữa hai đầu điện trở thuần và điện áp giữa hai bản tụ điện có giá trị hiệu dụng bằng nhau. Phát biểu nào sau đây là sai?
A. Cường độ dòng điện qua mạch trễ pha ${\text{ }\!\!\pi\!\!\text{ }}/{\text{4}}\;$ so với điện áp giữa hai đầu đoạn mạch. B. Điện áp giữa hai đầu điện trở thuần sớm pha ${\text{ }\!\!\pi\!\!\text{ }}/{\text{4}}\;$ so với điện áp giữa hai đầu đoạn mạch. C. Cường độ dòng điện qua mạch sớm pha ${\text{ }\!\!\pi\!\!\text{ }}/{\text{4}}\;$ so với điện áp giữa hai đầu đoạn mạch. D. Điện áp giữa hai đầu điện trở thuần sớm pha ${\text{ }\!\!\pi\!\!\text{ }}/{\text{4}}\;$ so với điện áp giữa hai đầu đoạn mạch. |
| HD giải: Ta có: $\text{tan }\!\!\varphi\!\!\text{ =}\frac{-{{\text{U}}_{\text{C}}}}{{{\text{U}}_{\text{R}}}}\text{=}1\Rightarrow \text{ }\!\!\varphi\!\!\text{ =}-\frac{\text{ }\!\!\pi\!\!\text{ }}{4}\text{.}$ Do đó u chậm pha hơn i góc $\frac{\text{ }\!\!\pi\!\!\text{ }}{4}$suy ra A sai. Chọn A. | 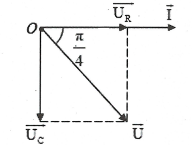 |
| Bài tập 7: [Trích đề thi Cao đẳng năm 2010] Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở thuần $\text{40 }\!\!\Omega\!\!\text{ }$và tụ điện mắc nối tiếp. Biết điện áp giữa hai đầu đoạn mạch lệch pha $\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$so với cường độ dòng điện trong đoạn mạch. Dung kháng của tụ điện bằng:
A. $\text{40}\sqrt{\text{3}}\text{ }\!\!\Omega\!\!\text{ }\text{.}$ B. $\frac{\text{40}\sqrt{\text{3}}}{3}\text{ }\!\!\Omega\!\!\text{ }\text{.}$ C. $\text{40 }\!\!\Omega\!\!\text{ }\text{. }$ D. $\text{ 20}\sqrt{\text{3}}\text{ }\!\!\Omega\!\!\text{ }\text{. }$ |
HD giải: Ta có $\text{tan}\frac{\pi }{3}\text{=}\frac{{{\text{Z}}_{\text{C}}}}{\text{R}}\Rightarrow {{\text{Z}}_{\text{C}}}\text{=R}\sqrt{\text{3}}\text{=40}\sqrt{\text{3}}\text{.}$ Chọn A.
| Bài tập 8: [Trích đề thi Cao đẳng năm 2010] Đặt điện áp $\text{u=}{{\text{U}}_{0}}\text{cos}\left( \text{ }\!\!\omega\!\!\text{ t}-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}} \right)\left( \text{V} \right)$vào hai đầu đoạn mạch gồm điện trở thuần R và cuộn cảm thuần có độ tự cảm L mắc nối tiếp thì cường độ dòng điện qua đoạn mạch là $\text{i=}{{\text{I}}_{\text{0}}}\sin \left( \text{ }\!\!\omega\!\!\text{ t}-\frac{\text{5 }\!\!\pi\!\!\text{ }}{12} \right)\left( \text{A} \right)$. Tỉ số điện trở thuần R và cảm kháng của cuộn cảm là:
A. $\frac{1}{2}.$ B. 1. C. $\frac{\sqrt{3}}{2}$. D. $\sqrt{3}$. |
HD giải: Ta có: ${{\text{ }\!\!\varphi\!\!\text{ }}_{u}}-{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{i}}}=\frac{\text{- }\!\!\pi\!\!\text{ }}{\text{6}}\text{+}\frac{\text{5 }\!\!\pi\!\!\text{ }}{\text{12}}\text{=}\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}.$ Do đó $\tan \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}=\frac{{{\text{Z}}_{\text{L}}}}{\text{R}}\Rightarrow \frac{{{\text{Z}}_{\text{L}}}}{\text{R}}=1\Rightarrow \frac{\text{R}}{{{\text{Z}}_{\text{L}}}}\text{=1}\text{.}$ Chọn B.
| Bài tập 9: Khi đặt vào hai đầu đoạn mạch gồm cuộn dây thuần cảm (cảm thuần) mắc nối tiếp với điện trở thuần một hiệu điện thế xoay chiều thì cảm kháng của cuộn dây bằng $\sqrt{3}$lần giá trị của điện trở thuần. Pha của dòng điện trong đoạn mạch so với pha hiệu điện thế giữa hai đầu đoạn mạch là:
A. chậm hơn góc $\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$. B. Nhanh hơn góc $\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$. C. Nhanh hơn góc $\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$. D. Chậm hơn góc $\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$. |
| HD giải: Ta có: $\tan \text{ }\!\!\varphi\!\!\text{ }=\frac{{{\text{Z}}_{\text{L}}}}{\text{R}}=\sqrt{3}\Rightarrow \text{ }\!\!\varphi\!\!\text{ }=\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$nên u nhanh pha hơn i góc $\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$hay dòng điện chậm pha hơn $\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$ so với điện áp hai đầu mạch. Chọn A. | 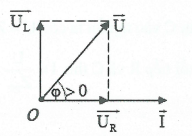 |
| Bài tập 10: Một đoạn mạch gồm cuộn dây thuần cảm (cảm thuần) mắc nối tiếp với điện trở thuần. Nếu đặt hiện điện thế $\text{u=15}\sqrt{\text{2}}\text{sin100 }\!\!\pi\!\!\text{ t}\left( \text{V} \right)$vào hai đầu đoạn mạch thì hiệu điện thế hiệu dụng giữa hai đầu cuộn dây là 5 V. Khi đó, hiệu điện thế hiệu dụng giữa hai đầu điện trở bằng:
A. $\text{5}\sqrt{\text{2}}\text{ V}\text{.}$ B. $\text{5}\sqrt{3}\text{ V}\text{.}$ C. $\text{10}\sqrt{\text{2}}\text{ V}\text{.}$ D. $\text{10}\sqrt{3}\text{ V}\text{.}$ |
HD giải: Ta có: $\text{U=15}\text{.}$
Mạch điện gồm điện trở và cuộn dây thuần cảm nên ${{\text{U}}^{\text{2}}}\text{=U}_{\text{R}}^{\text{2}}\text{+U}_{\text{L}}^{\text{2}}\Rightarrow {{\text{U}}_{\text{R}}}\text{=}\sqrt{{{\text{U}}^{\text{2}}}-\text{U}_{\text{L}}^{\text{2}}}$
$=\sqrt{{{15}^{2}}-{{5}^{2}}}=\text{10}\sqrt{\text{2}}\text{ V}\text{.}$ Chọn C.
| Bài tập 11: [Trích đề thi Đại học năm 2007] Trong một đoạn mạch xoay chiều không phân nhánh, cường độ dòng điện sớm pha $\text{ }\!\!\varphi\!\!\text{ }$(với $\text{0 }\!\!\varphi\!\!\text{ 0,5 }\!\!\pi\!\!\text{ }$) so với hiệu điện thế ở hai đầu đoạn mạch. Đoạn mạch đó:
A. gồm điện trở thuần và tụ điện. B. chỉ có cuộn cảm. C. gồm cuộn thuần cảm (cảm thuần) và tụ điện. D. gồm điện trở thuần và cuộn thuần cảm (cảm thuần). |
HD giải: Cường độ dòng điện sớm pha $\text{ }\!\!\varphi\!\!\text{ }$so với hiệu điện thế và $\text{0 }\!\!\varphi\!\!\text{ 0,5 }\!\!\pi\!\!\text{ }$ nên mạch đó gồm điện trở thuần và tụ điện. Chọn A.
| Bài tập 12: [Trích đề thi Cao đẳng năm 2007] Đặt hiệu điện thế $\text{u=125}\sqrt{\text{2}}\text{sin100 }\!\!\pi\!\!\text{ t}\left( \text{V} \right)$lên hai đầu một đoạn mạch gồm điện trở thuần $\text{R = 30 }\!\!\Omega\!\!\text{ }$, cuộn dây thuần cảm (cảm thuần) có độ tự cảm $\text{L = }\frac{\text{0,4}}{\text{ }\!\!\pi\!\!\text{ }}\left( \text{H} \right)$và ampe kế nhiệt mắc nối tiếp. Biết ampe kế có điện trở không đáng kể. Số chỉ của ampe kế là:
A. 2,0 A. B. 2,5 A. C. 3,5 A. D. 1,8 A. |
HD giải: Ta có: ${{\text{Z}}_{\text{L}}}\text{= L }\!\!\omega\!\!\text{ = 40 }\!\!\Omega\!\!\text{ }\text{.}$
Mạch gồm điện trở thuần và cuộn cảm thuần ta có: ${{\text{Z}}_{\text{RL}}}\text{=}\sqrt{\text{Z}_{\text{L}}^{\text{2}}\text{+}{{\text{R}}^{\text{2}}}}\text{=50 }\!\!\Omega\!\!\text{ }\text{.}$
Cường độ dòng điện trong mạch là $\text{I=}\frac{\text{U}}{\text{Z}}\text{=}\frac{\text{125}}{\text{50}}\text{=2,5A}$ Chọn B.
| Bài tập 13: Cho một nguồn xoay chiều ổn định. Nếu mắc vào nguồn một điện trở thuần R thì dòng điện qua R có giá trị hiệu dụng ${{\text{I}}_{\text{1}}}\text{=}\sqrt{\text{3}}\text{A}$. Nếu mắc tụ C vào nguồn thì được dòng điện có cường độ hiệu dụng ${{\text{I}}_{\text{2}}}\text{=1A}$. Nếu mắc R và C nối tiếp rồi mắc vào nguồn trên thì dòng điện qua mạch có giá trị hiệu dụng là;
A. 1 A. B. 0,5 A. C. 2 A. D. $\frac{\sqrt{3}}{2}\text{A}$. |
HD giải: Ban đầu mạch chỉ gồm điện trở thuần ta có: $\text{U=}{{\text{I}}_{\text{1}}}\text{R}\Rightarrow \text{R=}\frac{\text{U}}{\sqrt{\text{3}}}\text{.}$
Nếu mắc tụ C vào nguồn ta có: $\text{U=}{{\text{Z}}_{\text{C}}}\text{.}{{\text{I}}_{\text{2}}}\Rightarrow {{\text{Z}}_{\text{C}}}\text{=U}\text{.}$
Khi mắc nối tiếp R và C thì: $\text{I=}\frac{\text{U}}{{{\text{Z}}_{\text{RC}}}}\text{=}\frac{\text{U}}{\sqrt{{{\text{R}}^{\text{2}}}\text{+Z}_{\text{C}}^{\text{2}}}}\text{=}\frac{\text{U}}{\sqrt{\frac{{{\text{U}}^{\text{2}}}}{\text{3}}\text{+}{{\text{U}}^{\text{2}}}}}\text{=}\frac{\sqrt{\text{3}}}{\text{2}}\text{A}$ Chọn D.
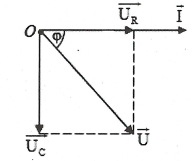
| Bài tập 14: Cho mạch điện xoay chiều nối tiếp R, C. Đặt vào hai đầu đoạn mạch một hiệu điện thế $\text{u=120}\sqrt{\text{2}}\text{cos}\left( \text{100 }\!\!\pi\!\!\text{ t} \right)\text{V}$thì ${{\text{Z}}_{\text{C}}}\text{=}{\text{R}}/{\sqrt{\text{3}}}\;\text{.}$Tại thời điểm t = 1/150s thì hiệu điện thế trên tụ có giá trị bằng:
A. $\text{30}\sqrt{\text{6}}\text{V}\text{.}$ B. $\text{30}\sqrt{\text{2}}\text{V}\text{.}$ C. $\text{60}\sqrt{\text{2}}\text{V}\text{.}$ D. $\text{0V}\text{.}$ |
| HD giải: Ta có: $\text{tan }\!\!\varphi\!\!\text{ =}\frac{{{\text{Z}}_{\text{C}}}}{\text{R}}\text{=}\frac{{{\text{U}}_{\text{C}}}}{{{\text{U}}_{\text{R}}}}\text{=}\frac{\text{1}}{\sqrt{\text{3}}}\Rightarrow \text{ }\!\!\varphi\!\!\text{ }=30{}^\circ .$
Do đó ${{\text{U}}_{\text{0C}}}\text{=}{{\text{U}}_{\text{0}}}\text{sin30 }\!\!{}^\circ\!\!\text{ =60}\sqrt{\text{2}}\text{. }$ Điện áp trên tụ chậm pha hơn điện áp hai đầu mạch góc $\text{ 60}{}^\circ $suy ra ${{\text{u}}_{\text{C}}}=60\sqrt{\text{2}}\text{cos}\left( \text{100 }\!\!\pi\!\!\text{ t}-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}} \right)\left( \text{V} \right).$ Tại $\text{t=}{\text{1}}/{\text{150 s}\Rightarrow {{\text{u}}_{\text{C}}}}\;=60\sqrt{2}\text{cos}\left( \text{100 }\!\!\pi\!\!\text{ t}\text{.}\frac{1}{150}-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}} \right)=3\text{0}\sqrt{\text{2}}\text{V}.$ Chọn B.
|
 |
| Bài tập 15: Một đoạn mạch điện gồm cuộn dây thuần cảm có độ tự cảm $\text{L=}{\text{0,5}}/{\text{ }\!\!\pi\!\!\text{ }\left( \text{H} \right)}\;$mắc nối tiếp với điện trở thuần $R=50\sqrt{3}\Omega .$ Đặt vào hai đầu đoạn mạch một điện áp xoay chiều thì dòng điện trong mạch có biểu thức là $\text{i=2cos}\left( \text{100 }\!\!\pi\!\!\text{ t + }\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}} \right)\left( \text{A} \right)$. Biểu thứ nào sau đây là của điện áp hai đầu đoạn mạch:
A. $\text{u=200cos}\left( \text{100 }\!\!\pi\!\!\text{ t + }\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}} \right)\text{V}$ B. $\text{u=200cos}\left( \text{100 }\!\!\pi\!\!\text{ t + }\frac{\text{ }\!\!\pi\!\!\text{ }}{6} \right)\text{V}\text{.}$ C. $\text{u=100}\sqrt{2}\text{cos}\left( \text{100 }\!\!\pi\!\!\text{ t + }\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right)\text{V}$. D. $\text{ u=200cos}\left( \text{100 }\!\!\pi\!\!\text{ t + }\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right)\text{V}\text{.}$ |
| HD giải: Ta có: ${{\text{Z}}_{\text{L}}}\text{=L }\!\!\omega\!\!\text{ =50 }\!\!\Omega\!\!\text{ }\text{.}$
Lại có: $\text{tan }\!\!\varphi\!\!\text{ =}\frac{{{\text{Z}}_{\text{L}}}}{\text{R}}\text{=}\frac{\text{1}}{\sqrt{\text{3}}}\Rightarrow \text{ }\!\!\varphi\!\!\text{ }=\frac{\pi }{6}\Rightarrow {{\text{ }\!\!\varphi\!\!\text{ }}_{\text{u}}}=\frac{\pi }{6}+\frac{\pi }{3}=\frac{\pi }{2}.$ Mặt khác: ${{\text{Z}}_{\text{RL}}}\text{=}\sqrt{{{\text{R}}^{\text{2}}}\text{+Z}_{\text{L}}^{\text{2}}}\text{=100}\Rightarrow {{\text{U}}_{\text{0}}}\text{=}{{\text{I}}_{\text{0}}}{{\text{Z}}_{\text{RL}}}\text{=200 }\!\!\Omega\!\!\text{ }\text{.}$ Do đó $\text{u=200cos}\left( \text{100 }\!\!\pi\!\!\text{ t + }\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right)\text{V}$. Chọn D.
|
 |
| Bài tập 16: Cho một đoạn mạch điện xoay chiều gồm cuộn cảm thuần L và điện trở R. Nếu đặt vào hai đầu đoạn mạch điện áp $\text{u=100cos}\left( \text{100 }\!\!\pi\!\!\text{ t} \right)\left( \text{V} \right)$thì cường độ dòng điện trong mạch là $\text{i=}\sqrt{2}\text{cos}\left( \text{100 }\!\!\pi\!\!\text{ t }-\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)\left( \text{A} \right)$. Giá trị của R và L là:
A. $\text{R=50 }\!\!\Omega\!\!\text{ , L=}\frac{\text{1}}{\text{2 }\!\!\pi\!\!\text{ }}\text{H}\text{.}$ B. $\text{R=50 }\!\!\Omega\!\!\text{ , L=}\frac{\sqrt{3}}{\text{ }\!\!\pi\!\!\text{ }}\text{H}\text{.}$ C. $\text{R=50 }\!\!\Omega\!\!\text{ , L=}\frac{\text{1}}{\text{ }\!\!\pi\!\!\text{ }}\left( \text{H} \right)\text{.}$ D. $\text{R=50}\sqrt{3}\text{ }\!\!\Omega\!\!\text{ , L=}\frac{\sqrt{3}}{\text{2 }\!\!\pi\!\!\text{ }}\left( \text{H} \right)$ |
| HD giải: Ta có: ${{\text{ }\!\!\varphi\!\!\text{ }}_{{\text{u}}/{\text{i}}\;}}\text{=}\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}.$
Mặt khác ${{\text{Z}}_{\text{RL}}}\text{=}\frac{{{\text{U}}_{\text{0}}}}{{{\text{I}}_{\text{0}}}}\text{=50}\sqrt{\text{2}}\Rightarrow \text{R=}{{\text{Z}}_{\text{L}}}\text{=}\frac{{{\text{Z}}_{\text{RL}}}}{\sqrt{\text{2}}}\text{=50 }\!\!\Omega\!\!\text{ }\text{.}$ Do đó $\text{R=50 }\!\!\Omega\!\!\text{ },\text{L=}\frac{\text{1}}{\text{2 }\!\!\pi\!\!\text{ }}\left( \text{H} \right)\text{.}$ Chọn A.
|
 |
| Bài tập 17: Một đoạn mạch điện gồm một cuộn dây thuần cảm có độ tự cảm $\text{L=}{\text{1}}/{\text{ }\!\!\pi\!\!\text{ }}\;\left( \text{H} \right)$ và điện trở thuần $\text{R=100 }\!\!\Omega\!\!\text{ }$. Đặt vào hai đầu mạch một điện áp xoay chiều $\text{u=200cos}\left( \text{100 }\!\!\pi\!\!\text{ t + }{\text{ }\!\!\pi\!\!\text{ }}/{\text{4}}\; \right)\left( \text{V} \right)$thì biểu thức nào sau đây là của điện áp hai đầu cuộn cảm thuần:
A. ${{\text{u}}_{\text{L}}}\text{=100}\sqrt{2}\text{cos}\left( \text{100 }\!\!\pi\!\!\text{ t + }{\text{ }\!\!\pi\!\!\text{ }}/{\text{4}}\; \right)\text{V}\text{.}$ B. ${{\text{u}}_{\text{L}}}\text{=100cos}\left( \text{100 }\!\!\pi\!\!\text{ t + }{\text{ }\!\!\pi\!\!\text{ }}/{2}\; \right)\text{V}\text{.}$ C. ${{\text{u}}_{\text{L}}}\text{=100}\sqrt{2}\text{cos}\left( \text{100 }\!\!\pi\!\!\text{ t}-{\text{ }\!\!\pi\!\!\text{ }}/{2}\; \right)\text{V}\text{.}$ D. ${{\text{u}}_{\text{L}}}\text{=100}\sqrt{2}\text{cos}\left( \text{100 }\!\!\pi\!\!\text{ t + }{\text{ }\!\!\pi\!\!\text{ }}/{2}\; \right)\text{V}\text{.}$ |
| HD giải: Ta có: ${{\text{Z}}_{\text{L}}}\text{=100 }\!\!\Omega\!\!\text{ , tan }\!\!\varphi\!\!\text{ =}\frac{{{\text{Z}}_{\text{L}}}}{\text{R}}\text{=1}\Rightarrow {{\text{ }\!\!\varphi\!\!\text{ }}_{{\text{u}}/{\text{i}}\;}}\text{=}\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}.$
$\Rightarrow {{\text{ }\!\!\varphi\!\!\text{ }}_{{\text{L}}/{\text{u}}\;}}\text{=}\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\Rightarrow {{\text{U}}_{\text{0L}}}\text{=}{{\text{U}}_{\text{0}}}\text{cos45 }\!\!{}^\circ\!\!\text{ =100}\sqrt{\text{2}}\text{V}\text{.}$ Do đó ${{\text{u}}_{\text{L}}}\text{=100}\sqrt{2}\text{cos}\left( \text{100 }\!\!\pi\!\!\text{ t + }{\text{ }\!\!\pi\!\!\text{ }}/{2}\; \right)\text{V}\text{.}$Chọn D.
|
 |
| Bài tập 18: Một đoạn mạch điện gồm tụ điện có điện dung $\text{C=}\frac{\text{1}{{\text{0}}^{\text{-4}}}}{\text{ }\!\!\pi\!\!\text{ }}\left( \text{F} \right)$và điện trở thuần $\text{R=100 }\!\!\Omega\!\!\text{ }$. Đặt vào hai đầu mạch một điện áp có biểu thức $\text{u=200}\sqrt{2}\text{cos}\left( \text{100 }\!\!\pi\!\!\text{ t }-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}} \right)\text{V}$ thì biểu thức của cường độ dòng điện trong mạch là:
A. $\text{i=}\sqrt{2}\text{cos}\left( \text{100 }\!\!\pi\!\!\text{ t }-\frac{\text{ }\!\!\pi\!\!\text{ }}{3} \right)\left( \text{A} \right)\text{.}$ B. $\text{i=}\sqrt{2}\text{cos100 }\!\!\pi\!\!\text{ t}\left( \text{A} \right)\text{.}$ C. $\text{i=2cos100 }\!\!\pi\!\!\text{ t}\left( \text{A} \right)\text{.}$ D. $\text{i=}2\text{cos}\left( \text{100 }\!\!\pi\!\!\text{ t }-\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right)\left( \text{A} \right)$. |
| HD giải: Ta có: ${{\text{Z}}_{\text{C}}}\text{=}\frac{\text{1}}{\text{C }\!\!\omega\!\!\text{ }}\text{=100 }\!\!\Omega\!\!\text{ }\text{.}$
Lại có: $\tan \text{ }\!\!\varphi\!\!\text{ }=\frac{-{{\text{Z}}_{\text{C}}}}{\text{R}}=-1\Rightarrow \text{ }\!\!\varphi\!\!\text{ }=-45{}^\circ ={{\text{ }\!\!\varphi\!\!\text{ }}_{\text{u}}}-{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{i}}}$ $\Rightarrow {{\text{ }\!\!\varphi\!\!\text{ }}_{\text{i}}}={{\text{ }\!\!\varphi\!\!\text{ }}_{\text{u}}}+45{}^\circ =0.$ Mặt khác $\text{Z=}\sqrt{{{\text{R}}^{\text{2}}}\text{+Z}_{\text{C}}^{\text{2}}}=100\sqrt{2}\Rightarrow {{\text{I}}_{\text{0}}}\text{=}\frac{{{\text{U}}_{\text{0}}}}{\text{Z}}\text{=2A}\text{.}$ Do đó $\text{i=2cos100 }\!\!\pi\!\!\text{ t}\left( \text{A} \right)\text{.}$Chọn C.
|
 |
| Bài tập 19: Hai cuộn dây nối tiếp với nhau trong một mạch điện xoay chiều. Cuộn 1 có điện trở thuần ${{\text{r}}_{\text{1}}}$ lớn gấp lần $\sqrt{3}$cảm kháng ${{\text{Z}}_{{{\text{L}}_{\text{1}}}}}$của nó, điện áp trên cuộn 1 và 2 có cùng giá trị hiệu dụng nhưng lệch pha nhau ${\text{ }\!\!\pi\!\!\text{ }}/{\text{3}}\;\text{ }$. Tỷ số độ tự cảm ${{{\text{L}}_{\text{1}}}}/{{{\text{L}}_{\text{2}}}}\;$của 2 cuộn dây:
A. 3/2. B. 1/3. C. 1/2. D. 2/3. |
HD giải: Ta có: $\tan {{\text{ }\!\!\varphi\!\!\text{ }}_{\text{1}}}\text{=}\frac{{{\text{Z}}_{{{\text{L}}_{\text{1}}}}}}{{{\text{r}}_{\text{1}}}}=\frac{1}{\sqrt{3}}\Rightarrow {{\text{ }\!\!\varphi\!\!\text{ }}_{\text{1}}}=\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\Rightarrow {{\text{ }\!\!\varphi\!\!\text{ }}_{2}}=\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}+\frac{\text{ }\!\!\pi\!\!\text{ }}{3}=\frac{\text{ }\!\!\pi\!\!\text{ }}{2}.$
(Chú ý nếu ${{\text{ }\!\!\varphi\!\!\text{ }}_{2}}=\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}-\frac{\text{ }\!\!\pi\!\!\text{ }}{3}=\frac{-\text{ }\!\!\pi\!\!\text{ }}{6}$loại vì cuộn dây có $\text{ }\!\!\varphi\!\!\text{ }>0$)
Suy ra cuộn 2 là cuộn cảm thuần ${{\text{U}}_{\text{1}}}\text{=}{{\text{U}}_{\text{2}}}\Rightarrow \sqrt{\text{r}_{1}^{2}\text{+Z}_{{{\text{L}}_{\text{1}}}}^{\text{2}}}={{\text{Z}}_{{{\text{L}}_{\text{2}}}}}$
$\Leftrightarrow \text{2}{{\text{Z}}_{{{\text{L}}_{\text{1}}}}}\text{=}{{\text{Z}}_{{{\text{L}}_{\text{2}}}}}\Rightarrow \frac{{{\text{L}}_{\text{1}}}}{{{\text{L}}_{\text{2}}}}\text{=}\frac{{{\text{Z}}_{{{\text{L}}_{\text{1}}}}}}{{{\text{Z}}_{{{\text{L}}_{\text{2}}}}}}\text{=}\frac{\text{1}}{\text{2}}.$ Chọn C.
| Bài tập 20: [Trích đề thi Đại học năm 2012] Khi đặt vào hai đầu một cuộn dây có độ tự cảm $\frac{\text{0,4}}{\text{ }\!\!\pi\!\!\text{ }}\left( \text{H} \right)$một hiệu điện thế một chiều 12 V thì cường độ dòng điện qua cuộn dây là 0,4 A. Sau đó, thay hiệu điện thế này bằng một điện áp xoay chiều có tần số 50 Hz và giá trị hiệu dụng 12 V thì cường độ dòng điện hiệu dụng qua cuộn dây bằng:
A. 0,30 A. B. 0,40 A. C. 0,24 A. D. 0,17 A. |
HD giải: Ta có: ${{\text{Z}}_{\text{L}}}\text{=L }\!\!\omega\!\!\text{ =40 }\!\!\Omega\!\!\text{ ,}$
Khi đặt hiệu điện thế một chiều vào hai đầu dây ta có: $\text{r=}\frac{\text{U}}{\text{I}}\text{=30 }\!\!\Omega\!\!\text{ }\text{.}$
Khi đặt điện áp xoay chiều vào hai đầu dây ta có: $\text{I=}\frac{\text{U}}{{{\text{Z}}_{\text{d}}}}\text{=}\frac{\text{U}}{\sqrt{{{\text{R}}^{\text{2}}}\text{+Z}_{\text{L}}^{\text{2}}}}\text{=}\frac{\text{12}}{\sqrt{\text{3}{{\text{0}}^{\text{2}}}\text{+4}{{\text{0}}^{\text{2}}}}}\text{= 0,24A}\text{.}$
Chọn C.
| Bài tập 21: [Trích đề thi chuyên Phan Bội Châu 2017] Cho một đoạn mạch gồm cuộn cảm thuần L và điện trở R mắc nối tiếp. Nếu mắc vào hai đầu đoạn mạch một điện áp xoay chiều $\text{u=100cos}\left( \text{100 }\!\!\pi\!\!\text{ t + }\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)\text{V}$thì dòng điện trong mạch có biểu thức $\text{i=}\sqrt{2}\text{cos}\left( \text{100 }\!\!\pi\!\!\text{ t} \right)\text{A}\text{.}$Giá trị của R và L là:
A. $\text{R=50 }\!\!\Omega\!\!\text{ , L=}\frac{\text{1}}{\text{2 }\!\!\pi\!\!\text{ }}\text{H}\text{.}$ B. $\text{R=50 }\!\!\Omega\!\!\text{ , L=}\frac{\text{1}}{\text{ }\!\!\pi\!\!\text{ }}\text{H}\text{.}$ C. $\text{R=50 }\!\!\Omega\!\!\text{ , L=}\frac{\sqrt{3}}{\text{ }\!\!\pi\!\!\text{ }}\text{H}\text{.}$ D. $\text{R=}200\text{ }\!\!\Omega\!\!\text{ , L=}\frac{2}{\text{ }\!\!\pi\!\!\text{ }}\text{H}\text{.}$ |
HD giải: Điện áp sớm pha ${\text{ }\!\!\pi\!\!\text{ }}/{\text{4}}\;$ so với dòng điện nên $\text{tan}\frac{\text{ }\!\!\pi\!\!\text{ }}{4}=\frac{{{\text{Z}}_{\text{L}}}}{\text{R}}=1\Rightarrow {{\text{Z}}_{\text{L}}}=\text{R}$
Tổng trở của mạch $\text{Z}=\sqrt{{{\text{R}}^{\text{2}}}\text{+Z}_{\text{L}}^{\text{2}}}=\text{R}\sqrt{2}=50\sqrt{2}\Rightarrow \left\{ \begin{array}{} \text{R=50 }\!\!\Omega\!\!\text{ } \\ {} \text{L=}\frac{\text{1}}{\text{2 }\!\!\pi\!\!\text{ }}\text{H} \\ \end{array} \right.$. Chọn A.
