VẤN ĐÈ 1: DÒNG ĐIỆN KHÔNG ĐỔI. NGUỒN ĐIỆN. ĐỊNH LUẬT ÔM CHO ĐOẠN MẠCH CHÍ CHỨA ĐIỆN TRỞ.
LÝ THUYẾT TRỌNG TÂM
1. Dòng điện.
– Dòng điện là dòng các điện tích dịch chuyển có hướng.
– Chiều qui ước của dòng điện là chiều dịch chuyển của các điện tích dương tức là ngược chiều dịch chuyển của các electron.
– Các tác dụng của dòng điện: dòng điện có tác dụng nhiệt, tác dụng hoá học, tác dụng từ, tác dụng cơ và tác dụng sinh lí, trong đó tác dụng từ là tác dụng đặc trưng của dòng điện.
– Cường độ dòng điện đặc trưng cho tác dụng mạnh yếu của dòng điện và được xác định bằng thương số giữa điện lượng $\Delta q$ dịch chuyển qua tiết diện thẳng của vật dẫn trong khoảng thời gian $\Delta t$ và khoảng thời gian đó: $I=\frac{\Delta q}{\Delta t}$
– Dòng điện có chiều và cường độ không thay đổi theo thời gian gọi là dòng điện không đổi. Với
dòng điện không đổi ta có: $I=\frac{q}{t}$
– Điều kiện để có dòng điện trong một môi trường nào đó là trong môi trường đó phải có các điện tích tự do và phải có một điện trường để đẩy các điện tích tự do chuyển động có hướng. Trong vật dẫn điện có các điện tích tự do nên điều kiện để có dòng điện là phải có một hiệu điện thế đặt vào hai đầu vật dẫn điện.
2. Nguồn điện.
– Nguồn điện là thiết bị để tạo ra và duy trì hiệu điện thế nhằm duy trì dòng điện trong mạch.
– Nguồn điện có hai cực: cực dương (+) và cực âm (-).
– Các lực lạ (khác bản chất với lực điện) bên trong nguồn điện có tác dụng làm cho hai cực của nguồn điện được tích điện khác nhau và do đó duy trì hiệu điện thế giữa hai cực của nó.
– Suất điện động của nguồn điện đặc trưng cho khả năng thực hiện công của nguồn điện và được đo bằng công của lực lạ khi làm dịch chuyển một đơn vị điện tích dương ngược chiều điện trường bên trong nguồn điện: $\zeta =\frac{A}{q}$
– Đề đo suất điện động của nguồn ta dùng vôn kế mắc vào hai cực của nguồn điện khi mạch ngoài để hở.
– Điện trở r của nguồn điện được gọi là điện trở trong của nó.
3. Đoạn mạch chỉ chứa điện trở.
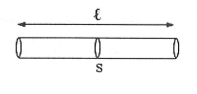
Điện trở: Điện trở của dây dẫn kim loại hình trụ: $R=\frac{\rho \ell }{S}$
Trong đó: $\ell $ là chiều dài (m)
S là tiết diện ngang $({{m}^{2}})$
$\rho $ là điện trở suất $(\Omega m)$.
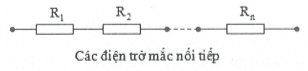
Ghép điện trở. Điện trở tương đương:
– Mạch điện mắc nối tiếp các điện trở:
$R={{R}_{1}}+{{R}_{2}}+…+{{R}_{n}}$
– Mạch điện mắc song song các điện trở:
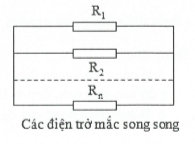$\frac{1}{R}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+…+\frac{1}{{{R}_{n}}}$
+) Nếu có 2 điện trở:
$\frac{1}{R}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}\Rightarrow R=\frac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}$
+) Nếu có $n-{{R}_{0}}$ giống nhau: $R=\frac{{{R}_{0}}}{n}$.
Định luật ôm cho đoạn mạch chứa điện trở: $R=\frac{U}{I}$
$\Rightarrow U=\text{IR}$ là độ giảm thế.
$\Rightarrow I=U/\text{R}\Rightarrow $ đồ thị cường độ dòng điện phụ thuộc vào hiệu điện thế đặt vào là một đường thẳng qua gốc tọa độ.
Mạch điện mắc nối tiếp các điện trở: Mạch điện mắc song song các điện trở:
$\left\{ \begin{array}{} R={{R}_{1}}+{{R}_{2}}+…+{{R}_{n}} \\ {} I={{I}_{1}}={{I}_{2}}=…={{I}_{n}} \\ {} U={{U}_{1}}+{{U}_{2}}+…+{{U}_{n}} \\ \end{array} \right.$ $\left\{ \begin{array}{} \frac{1}{R}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+…+\frac{1}{{{R}_{n}}} \\ {} \left\{ \begin{array}{} I={{I}_{1}}+{{I}_{2}}+…+{{I}_{n}} \\ {} U={{U}_{1}}={{U}_{2}}=…={{U}_{n}} \\ \end{array} \right. \\ \end{array} \right.$
4. Điện năng. Công suất điện.
– Điện năng, công suất tiêu thụ: $A=UIt$ ; $P=\frac{A}{t}=UI$
Trong đó:
A là điện năng tiêu thụ của đoạn mạch (J)
U là hiệu điện thế hai đầu đoạn mạch (V)
I là cường độ dòng điện qua đoạn mạch (A)
t là thời gian dòng điện chạy qua đoạn mạch (s).
P là công suất tiêu thụ của đoạn mạch (W).
– Công suất tỏa nhiệt trên điện trở R: $P=UI={{I}^{2}}R=\frac{{{U}^{2}}}{R}$
– Định luật Jun-Lenxo: Nhiệt lượng Q (J) tỏa ra trên một vật dẫn khi có dòng điện chạy qua tỉ lệ thuận với điện trở của vật dẫn, với bình phương cường độ dòng điện và với thời gian dòng điện chạy qua vật dẫn đó:
$Q={{I}^{2}}Rt$
– Công. Công suất của nguồn điện: ${{A}_{ng}}=\xi It$; $P=\frac{{{A}_{ng}}}{t}=\xi I$
CÁC DẠNG BÀI TẬP
DẠNG 1: ĐIỆN LƯỢNG. CƯỜNG ĐỘ DÒNG ĐIỆN. SUẤT ĐIỆN ĐỘNG CỦA NGUỒN ĐIỆN.
PHƯƠNG PHÁP GIẢI
– Cường độ dòng điện: $I=\frac{\Delta q}{\Delta t}$
Số electron: $n=\frac{\Delta q}{\left| e \right|}=\frac{I.t}{\left| e \right|}$
Trong đó:
$\Delta q$ là điện lượng dịch chuyển qua tiết diện thẳng của vật dẫn trong thời gian t (C).
I là cường độ dòng điện (A).
t là thời gian có điện lượng chuyển qua tiết diện thẳng (s).
n là số electron chuyển qua tiết diện thẳng của vật dẫn trong thời gian t.
– Suất điện động của nguồn: $\xi =\frac{A}{q}\Rightarrow A=\xi q=\xi It$
Trong đó:
A là công mà nguồn điện (công lực lạ), đơn vị là Jun (J);
q độ lớn điện tích, đơn vị là Cu-lông (C);
E là suất điện động của nguồn điện, đơn vị là Vôn (V).
BÀI TẬP LUYỆN TẬP DẠNG 1
| Bài tập 1: Một dây dẫn kim loại có các electron tự do chạy qua và tạo thành một dòng điện không đổi. Dây có tiết diện ngang $S=0,6m{{m}^{2}}$, trong thời gian 10 s có điện lượng $q=9,6 C$đi qua. Tính:
a) Cường độ dòng điện qua dây dẫn. b) Số electron đi qua tiết diện ngang của dây dẫn trong l0 s. |
Lời giải chi tiết
a) Cường độ dòng điện: $I=\frac{q}{t}=0,96 A$
b) Số electron đi qua tiết diện ngang của dây: $n=\frac{q}{\left| e \right|}={{6.10}^{19}}$.
| Bài tập 2: Trong khoảng thời gian 10s, dòng điện qua dây dẫn tăng đều từ ${{I}_{1}}=1 A$ đến ${{I}_{2}}=4 A$. Tính cường độ dòng điện trung bình và điện lượng qua dây trong thời gian trên. |
Lời giải chi tiết
Cường độ dòng điện trung bình: $I=\frac{{{I}_{1}}+{{I}_{2}}}{2}=\frac{1+4}{2}=2,5 A$
Điện lượng qua dây trong thời gian trên: $q=It=2,5.10=25 C$.
| Bài tập 3: Một bộ acquy cung cấp một dòng điện 5A liên tục trong 4 giờ thì phải nạp lại.
a) Tính cường độ dòng điện mà acquy này có thể cung cấp liên tục trong thời gian 12 giờ thì phải nạp lại. b) Tính suất điện động của acquy này nếu trong thời gian hoạt động trên nó sản sinh một công 1728 kJ. |
Lời giải chi tiết
a) Mỗi acquy có một dung lượng xác định. Dung lượng của mỗi acquy là điện lượng lớn nhất mà acquy có thể cung cấp được khi nó phát điện.
Dung lượng của acquy: $q=I.t\Rightarrow {{I}_{1}}{{t}_{1}}={{I}_{2}}{{t}_{2}}\Rightarrow {{I}_{2}}={{I}_{1}}\frac{{{t}_{1}}}{{{t}_{2}}}=\frac{5}{3} A$.
b) Suất điện động của nguồn điện: $\xi =\frac{A}{q}=\frac{A}{{{I}_{1}}{{t}_{1}}}=\frac{{{1728.10}^{3}}}{5.4.3600}=24 V$.
| Bài tập 4: Một bộ acquy có suất điện động 12V nối vào một mạch kín.
a) Tính lượng điện tích dịch chuyển ở giữa hai cực của nguồn điện để acquy sản ra công 720 J. b) Thời gian dịch chuyển lượng điện tích này là 5 phút. Tính cường độ dòng điện chạy qua acquy này. c) Tính số electron dịch chuyển qua tiết diện thẳng của dây dẫn trong thời gian 1 phút. |
Lời giải chi tiết
a) Ta có: $\xi =\frac{A}{q}=\Rightarrow q=\frac{A}{\xi }=\frac{720}{12}$=60C
b) Cường độ dòng điện: $I=\frac{A}{\xi t}=\frac{720}{12.5.60}=0,2 A$
c) Số electron dịch chuyển qua tiết diện thẳng của dây dẫn trong 1 phút:
${{N}_{e}}=\frac{q}{\left| e \right|}=\frac{It}{\left| e \right|}=\frac{0,2.60}{1,{{6.10}^{-19}}}=7,{{5.10}^{19}}$
DẠNG 2: ĐỊNH LUẬT ÔM CHO ĐOẠN MẠCH CHỈ CÓ R.
PHƯƠNG PHÁP GIẢI
Điện trở: Điện trở của dây dẫn kim loại hình trụ: $R=\frac{\rho \ell }{S}$
Trong đó: $\ell $ là chiều dài (m)
S là tiết diện ngang (${{m}^{2}}$)
$\rho $là điện trở suất $(\Omega m)$.
Ghép điện trở. Điện trở tương đương:
– Mạch điện mắc nối tiếp các điện trở:
$R={{R}_{1}}+{{R}_{2}}+…+{{R}_{n}}$
– Mạch điện mắc song song các điện trở:
$\frac{1}{R}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+…+\frac{1}{{{R}_{n}}}$
+) Nếu có 2 điện trở:
$\frac{1}{R}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}\Rightarrow R=\frac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}$
+) Nếu có $n-{{R}_{0}}$ giống nhau: $R=\frac{{{R}_{0}}}{n}$.
Định luật ôm cho đoạn mạch chứa điện trở: $R=\frac{U}{I}$
$\Rightarrow U=\text{IR}$ là độ giảm thế.
$\Rightarrow I=U/\text{R}\Rightarrow $ đồ thị cường độ dòng điện phụ thuộc vào hiệu điện thế đặt vào là một đường thẳng qua gốc tọa độ.
Mạch điện mắc nối tiếp các điện trở: Mạch điện mắc song song các điện trở:
$\left\{ \begin{array}{} R={{R}_{1}}+{{R}_{2}}+…+{{R}_{n}} \\ {} I={{I}_{1}}={{I}_{2}}=…={{I}_{n}} \\ {} U={{U}_{1}}+{{U}_{2}}+…+{{U}_{n}} \\ \end{array} \right.$ $\left\{ \begin{array}{} \frac{1}{R}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+…+\frac{1}{{{R}_{n}}} \\ {} \left\{ \begin{array}{} I={{I}_{1}}+{{I}_{2}}+…+{{I}_{n}} \\ {} U={{U}_{1}}={{U}_{2}}=…={{U}_{n}} \\ \end{array} \right. \\ \end{array} \right.$
BÀI TẬP LUYỆN TẬP DẠNG 2
| Bài tập 1: Một thỏi đồng có khối lượng 176 g được kéo thành dây dẫn có tiết diện tròn đường kính $d=0,36 mm$. Tính điện trở của dây dẫn. Cho biết khối lượng riêng của đồng là $8,{{8.10}^{3}} kg/{{m}^{3}}$ và điện trở suất của đồng bằng $1,{{6.10}^{-8}} \Omega m$. |
Lời giải chi tiết
Tiết diện tròn của sợi dây dẫn $S=\frac{\pi {{d}^{2}}}{4}$
Khối lượng thỏi đồng là $m=VD=S\ell D\Rightarrow \ell =\frac{m}{SD}$
Điện trở trên dây dẫn là $R=\frac{\rho \ell }{S}=\frac{\rho m}{{{S}^{2}}D}=\frac{16\rho m}{{{\pi }^{2}}{{d}^{4}}D}=\frac{16.1,{{6.10}^{-8}}.0,176}{10.{{\left( \frac{0,36}{1000} \right)}^{4}}.8,{{8.10}^{3}}}=30,5 \Omega $.
| Bài tập 2: Hai điện trở ${{R}_{1}}$, ${{R}_{2}}$ mắc vào hiệu điện thế $U=12 V$. Lần đầu ${{R}_{1}}$, ${{R}_{2}}$mắc song song, dòng điện mạch chính${{I}_{s}}=10 A$. Lần sau ${{R}_{1}}$, ${{R}_{2}}$ mắc nối tiếp, dòng điện trong mạch${{I}_{n}}=2,4 A$. Tìm ${{R}_{1}}$, ${{R}_{2}}$. |
Lời giải chi tiết
Điện trở tương đương của đoạn mạch khi :
$\left[ {{R}_{1}}// {{R}_{2}} \right]: {{R}_{ss}}=\frac{{{R}_{1}}{{R}_{1}}}{{{R}_{1}}+{{R}_{2}}}=\frac{U}{{{I}_{ss}}}=\frac{12}{10}=1,2$ (1)
$\left[ {{R}_{1}} nt {{R}_{2}} \right]: {{R}_{n}}={{R}_{1}}+{{R}_{2}}=\frac{U}{{{I}_{nt}}}=\frac{12}{2,4}=5$ (2)
Thay (2) vào (1) ta được: ${{R}_{1}}{{R}_{2}}=1,2.5=6$ (3)
Từ (2) suy ra: ${{R}_{2}}=5-{{R}_{1}}$ (4)
Thay (4) vào (3) ta được: ${{R}_{1}}.(5-{{R}_{1}})=6$
$\Leftrightarrow R_{1}^{2}-5{{R}_{1}}+6=0\Rightarrow \left[ \begin{array}{} {{R}_{1}}=3\Omega \\ {} {{R}_{1}}=2\Omega \\ \end{array} \right.\Rightarrow \left[ \begin{array}{} {{R}_{2}}=2\Omega \\ {} {{R}_{2}}=3\Omega \\ \end{array} \right.$
Vậy có hai giá trị của ${{R}_{1}}$và ${{R}_{2}}$là $\left( {{R}_{1}}=3 \Omega ; {{R}_{2}}=2 \Omega \right)$ hoặc $\left( {{R}_{1}}=2 \Omega ; {{R}_{2}}=3 \Omega \right)$.
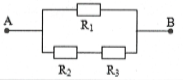
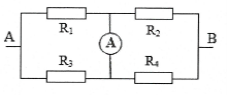
| Bài tập 3: Cho mạch điện như hình vẽ: ${{R}_{1}}=12 \Omega $, ${{R}_{2}}=15 \Omega $, ${{R}_{3}}=5 \Omega $, cường độ qua mạch chính $I=2 A$. Tìm cường độ dòng điện qua từng điện trở.
|
Lời giải chi tiết
Ta có: ${{R}_{23}}={{R}_{2}}+{{R}_{3}}=15+5=20 \Omega \Rightarrow {{R}_{AB}}=\frac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}=\frac{12.20}{12+20}=7,5 \Omega $
Hiệu điện thế giữa hai đầu đoạn mạch AB: ${{U}_{AB}}=I{{R}_{AB}}=2.7,5=15 V$.
Cường độ dòng điện qua điện trở ${{R}_{1}}$, ${{R}_{2}}$, ${{R}_{3}}$ lần lượt là:
${{I}_{1}}=\frac{{{U}_{AB}}}{{{R}_{1}}}=\frac{15}{12}=1,25 A; {{I}_{2}}={{I}_{3}}=\frac{{{U}_{AB}}}{{{R}_{23}}}=0,75 A$.
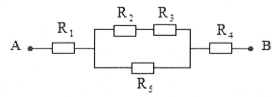
| Bài tập 4: Cho mạch điện như hình vẽ. Biết ${{R}_{1}}={{R}_{2}}=4 \Omega $, ${{R}_{3}}=6 \Omega $, ${{R}_{4}}=3 \Omega $, ${{R}_{5}}=10 \Omega $, ${{U}_{AB}}=24 V$. Tính cường độ dòng điện qua điện trở ${{R}_{2}}$.
|
Lời giải chi tiết
Ta có ${{R}_{23}}={{R}_{2}}+{{R}_{3}}=4+6=10 \Omega \Rightarrow {{R}_{235}}=\frac{{{R}_{23}}{{R}_{5}}}{{{R}_{23}}+{{R}_{5}}}=\frac{10.10}{10+10}=5 \Omega $;
${{R}_{td}}={{R}_{1}}+{{R}_{235}}+{{R}_{4}}=4+5+3=12 \Omega $
Cường độ dòng điện trong mạch chính là ${{I}_{c}}=\frac{{{U}_{AB}}}{{{R}_{c}}}=\frac{24}{12}=2 A={{I}_{235}}$
$\Rightarrow {{U}_{235}}={{I}_{235}}{{R}_{235}}=2.5=10 V={{U}_{23}}$
$\Rightarrow {{I}_{23}}=\frac{{{U}_{23}}}{{{R}_{23}}}=\frac{10}{10}=1 A={{I}_{2}}$
Vậy cường độ dòng điện qua điện trở ${{R}_{2}}$ là 1 A.
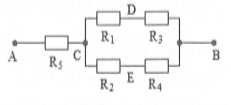
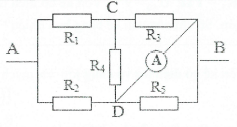
| Bài tập 5: Cho đoạn mạch như hình vẽ:${{R}_{1}}={{R}_{3}}=3 \Omega $, ${{R}_{2}}=2 \Omega $, ${{R}_{4}}=1 \Omega $, $ {{R}_{5}}=4 \Omega $, cường độ qua mạch chính $I=3 A$. Tìm:
a) ${{U}_{AB}}$ b) Hiệu điện thế hai đầu mỗi điện trở. c) ${{U}_{AD}}, {{U}_{ED}}$. d) Nối D, E bằng tụ điện $C=2\mu F$. Tìm điện tích của tụ. |
Lời giải chi tiết
a) ${{R}_{13}}={{R}_{1}}+{{R}_{3}}=3+3=6 \Omega $; ${{R}_{24}}={{R}_{2}}+{{R}_{4}}=2+1=3 \Omega $
$\Rightarrow {{R}_{CB}}=\frac{{{R}_{13}}{{R}_{24}}}{{{R}_{13}}+{{R}_{24}}}=\frac{6.3}{6+3}=2 \Omega $
$\Rightarrow {{R}_{AB}}={{R}_{5}}+{{R}_{CB}}=4+2=6 \Omega $.
Hiệu điện thế hai đầu đoạn mạch AB: ${{U}_{AB}}=I{{R}_{AB}}=3.6=18 V$
b) Ta có: ${{U}_{5}}=I{{R}_{5}}=3.4=12 V$; ${{U}_{CB}}=I{{R}_{CB}}=3.2=6 V$
Cường độ dòng điện qua ${{R}_{1}}, {{R}_{3}}$: ${{I}_{1}}={{I}_{3}}=\frac{{{U}_{CB}}}{{{R}_{13}}}=\frac{6}{6}=1 A$
$\Rightarrow {{U}_{1}}={{I}_{1}}{{R}_{1}}=1.3=3 V$; ${{U}_{3}}={{I}_{3}}{{R}_{3}}=1.3=3 V$.
Cường độ dòng điện qua ${{R}_{2}}, {{R}_{4}}$: ${{I}_{2}}={{I}_{4}}=\frac{{{U}_{CB}}}{{{R}_{24}}}=\frac{6}{3}=2 A$
$\Rightarrow {{U}_{2}}={{I}_{2}}{{R}_{2}}=2.2=4 V$; ${{U}_{4}}={{I}_{4}}{{R}_{4}}=2.1=2V$.
c) ${{U}_{AD}}={{U}_{AC}}+{{U}_{CD}}={{U}_{5}}+{{U}_{1}}=12+3=15 V$
${{U}_{ED}}={{U}_{EB}}+{{U}_{BD}}={{U}_{4}}-{{U}_{3}}=2-3=-1 V$.
d) Ta có: $Q=CU={{2.10}^{-6}}.1={{2.10}^{-6}} C$.
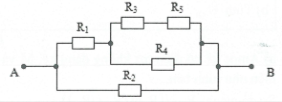
| Bài tập 6: Cho mạch điện như hình vẽ: ${{R}_{1}}=10 \Omega $, ${{R}_{2}}=6 \Omega $, ${{R}_{3}}=2 \Omega $, ${{R}_{4}}=3 \Omega $, ${{R}_{5}}=4 \Omega $. Cường độ đòng điện qua ${{R}_{3}}$ là 0,5 A.
Tìm cường độ qua từng điện trở và ${{U}_{AB}}$. |
Lời giải chi tiết
Ta có: ${{R}_{35}}={{R}_{3}}+{{R}_{5}}=2+4=6 \Omega $
$\Rightarrow {{U}_{35}}={{U}_{4}}={{I}_{3}}{{R}_{35}}=0,5.6=3 V \Rightarrow {{I}_{3}}={{I}_{5}}=0,5 A; {{I}_{4}}=\frac{{{U}_{4}}}{{{R}_{4}}}=\frac{3}{3}=1 A$
$\Rightarrow {{I}_{1}}={{I}_{3}}+{{I}_{4}}=0,5+1=1,5 A \Rightarrow {{U}_{1}}={{I}_{1}}{{R}_{1}}=1,5.10 = 15 V$
Hiệu điện thế hai đầu AB: ${{U}_{AB}}={{U}_{1}}+{{U}_{35}}=15+3=18 V$
Cường độ dòng điện qua ${{R}_{2}}$: ${{I}_{2}}=\frac{{{U}_{AB}}}{{{R}_{2}}}=\frac{18}{6}=3 A$.
| Bài tập 7: Cho mạch điện như hình vẽ. Biết ${{R}_{1}}=15 \Omega $, ${{R}_{2}}=30 \Omega $, ${{R}_{3}}=45 \Omega $, ${{R}_{4}}=10 \Omega $, ${{R}_{A}}=0$, ${{U}_{AB}}=75 V$.
a) Tính điện trở toàn mạch. b) Số chỉ của ampe kế bằng bao nhiêu? |
Lời giải chi tiết
a) Vì ampe kế có điện trở không đáng kể nên ta chập M với N, vẽ lại mạch điện như hình bên. Sơ đồ mạch: $({{R}_{1}}// {{R}_{3}}) nt ({{R}_{2}}// {{R}_{4}})$
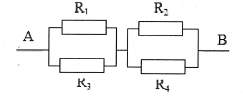${{R}_{13}}=\frac{{{R}_{1}}{{R}_{3}}}{{{R}_{1}}+{{R}_{3}}}=\frac{15.45}{15+45}=11,25 \Omega $;
${{R}_{24}}=\frac{{{R}_{2}}{{R}_{4}}}{{{R}_{2}}+{{R}_{4}}}=\frac{30.10}{30+10}=7,5 \Omega $
${{R}_{AB}}={{R}_{13}}+{{R}_{24}}=11,25+7,5=18,75 \Omega $
b) Cường độ dòng điện trong mạch chính: ${{I}_{c}}=\frac{{{U}_{AB}}}{{{R}_{AB}}}=\frac{75}{18,75}=4 A={{I}_{13}}={{I}_{24}}$
$\Rightarrow {{U}_{13}}={{I}_{13}}{{R}_{13}}=4.11,25=45 V={{U}_{1}} \Rightarrow {{I}_{1}}=\frac{{{U}_{1}}}{{{R}_{1}}}=\frac{45}{15}=3 A$
$\Rightarrow {{U}_{24}}={{I}_{24}}{{R}_{24}}=4.7,5=30 V={{U}_{2}} \Rightarrow {{I}_{2}}=\frac{{{U}_{21}}}{{{R}_{2}}}=\frac{30}{30}=1 A$
Do ${{I}_{1}}>{{I}_{2}}\Rightarrow {{I}_{1}}={{I}_{A}}+{{I}_{2}}\Rightarrow {{I}_{A}}={{I}_{1}}-{{I}_{2}}=3-1=2 A$.
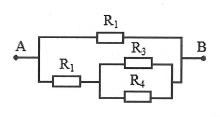
| Bài tập 8: Cho mạch điện như hình vẽ. Biết ${{R}_{1}}=15 \Omega $, ${{R}_{2}}={{R}_{3}}={{R}_{4}}=10 \Omega $. Điện trở của ampe kế và dây nối không đáng kể. Biết ampe kế chỉ 3 A.
a) Tính điện trở tương đương của đoạn mạch. b) Tính ${{U}_{AB}}$. |
Lời giải chi tiết
a)Ampe kế có điện trở không đáng kể, M và B có cùng điện thế nên chập M với B ta được mạch điện như hình bên.
Sơ đồ mạch: ${{R}_{1}}//\left( {{R}_{2}} nt \left( {{R}_{3}}// {{R}_{4}} \right) \right)$
Ta có: ${{R}_{34}}=\frac{{{R}_{3}}{{R}_{4}}}{{{R}_{3}}+{{R}_{4}}}=\frac{10.10}{10+10}=5 \Omega $;
${{R}_{234}}={{R}_{2}}+{{R}_{34}}=10+5=15 \Omega $
${{R}_{AB}}=\frac{{{R}_{1}}{{R}_{234}}}{{{R}_{1}}+{{R}_{234}}}=\frac{10.15}{10+15}=6 \Omega $
b) Giả sử dòng điện đi qua ${{R}_{3}}$ có chiều từ M đến N $\Rightarrow {{I}_{1}}+{{I}_{3}}={{I}_{A}}=3 A (1)$
Gọi hiệu điện thế hai đầu mạch là ${{U}_{AB}}\Rightarrow {{U}_{1}}={{U}_{234}}={{U}_{AB}}$
$\Rightarrow {{I}_{1}}=\frac{{{U}_{1}}}{{{R}_{1}}}=\frac{{{U}_{AB}}}{15} A (2)$
Lại có: ${{I}_{34}}={{I}_{2}}={{I}_{234}}=\frac{{{U}_{AB}}}{{{R}_{234}}}=\frac{{{U}_{AB}}}{15} A\Rightarrow {{U}_{34}}={{I}_{34}}{{R}_{34}}=\frac{{{U}_{AB}}}{15}.5=\frac{{{U}_{AB}}}{3} V={{U}_{3}}$
$\Rightarrow {{I}_{3}}=\frac{{{U}_{3}}}{{{R}_{3}}}=\frac{{{U}_{AB}}}{3.10}=\frac{{{U}_{AB}}}{30} A (3)$
Từ (1), (2), (3)$\Rightarrow \frac{{{U}_{AB}}}{15}+\frac{{{U}_{AB}}}{30}=3\Rightarrow {{U}_{AB}}=30 V$.
| Bài tập 9: Cho mạch điện như hình vẽ. Biết ${{U}_{AB}}=30 V$, ${{R}_{1}}={{R}_{2}}={{R}_{3}}={{R}_{4}}={{R}_{5}}=10 \Omega $. Điện trở của ampe kế không đáng kể.
a) Tính điện trở toàn mạch. b) Tìm chỉ số của ampe kế. |
Lời giải chi tiết
a) Ampe kế có điện trở không đáng kể $\Rightarrow $ chập $B\equiv D$. Ta vẽ lại mạch điện như hình bên. Sơ đồ mạch: ${{R}_{2}}//\left( {{R}_{1}} nt \left( {{R}_{3}}// {{R}_{4}} \right) \right)$
${{R}_{34}}=\frac{{{R}_{3}}{{R}_{4}}}{{{R}_{3}}+{{R}_{4}}}=\frac{10.10}{10+10}=5 \Omega $;
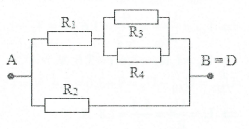
${{R}_{134}}={{R}_{1}}+{{R}_{34}}=10+5=15 \Omega $
${{R}_{AB}}=\frac{{{R}_{2}}.{{R}_{134}}}{{{R}_{2}}+{{R}_{134}}}=\frac{10.15}{10+15}=6 \Omega $
b) Giả sử dòng điện đi qua ampe kế có chiều từ D đến B $\Rightarrow {{I}_{2}}+{{I}_{4}}={{I}_{A}} (1)$
Ta có: ${{U}_{2}}={{U}_{134}}={{U}_{AB}}=30 V$
${{I}_{2}}=\frac{{{U}_{2}}}{{{R}_{2}}}=\frac{30}{10}=3 A (2)$
${{I}_{134}}=\frac{{{U}_{134}}}{{{R}_{134}}}=\frac{30}{15}=2 A={{I}_{1}}={{I}_{34}}$
$\Rightarrow {{U}_{34}}={{I}_{34}}{{R}_{34}}=2.5=10 V={{U}_{3}}={{U}_{4}}\Rightarrow {{I}_{4}}=\frac{{{U}_{4}}}{{{R}_{4}}}=\frac{10}{10}=1 A (3)$
Từ (1), (2), (3)$\Rightarrow {{I}_{A}}=3+1=4 A$.
Bài tập 10: Cho mạch điện một chiều như hình vẽ, trong đó: ${{R}_{1}}=1 \Omega $, ${{R}_{2}}=4 \Omega $, ${{R}_{3}}=1 \Omega $, ${{R}_{4}}=2 \Omega $, ${{R}_{V}}=\infty $, ${{U}_{AB}}=12 V$. Tính ${{U}_{MN}}$.  |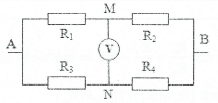
Lời giải chi tiết
Do ${{R}_{V}}=\infty \Rightarrow $ sơ đồ mạch $\left( {{R}_{1}} nt {{R}_{2}} \right)//\left( {{R}_{3}} nt {{R}_{4}} \right)$
${{R}_{12}}={{R}_{1}}+{{R}_{2}}=1+4=5 \Omega $; ${{R}_{34}}={{R}_{3}}+{{R}_{4}}=1+2=3 \Omega $
Ta có: ${{U}_{12}}={{U}_{34}}={{U}_{AB}}=12 V$
$\Rightarrow {{I}_{12}}=\frac{{{U}_{12}}}{{{R}_{12}}}=\frac{12}{5}=2,4 \Alpha ={{\Iota }_{1}}\Rightarrow {{U}_{1}}={{I}_{1}}{{R}_{1}}=2,4.1=2,4 V={{U}_{AM}}$
$\Rightarrow {{I}_{34}}=\frac{{{U}_{34}}}{{{R}_{34}}}=\frac{12}{3}=4 \Alpha ={{\Iota }_{3}}\Rightarrow {{U}_{3}}={{I}_{3}}{{R}_{3}}=4.1=4 V={{U}_{AN}}$
$\Rightarrow {{U}_{MN}}={{U}_{MA}}+{{U}_{AN}}=-{{U}_{AM}}+{{U}_{AN}}=-2,4+4=1,6 V$.
