Bài tập biểu diễn hình học của số phức có đáp án.
Dưới dây là một số bài tập trắc nghiệm biểu diễn hình học của số phức có Lời giải chi tiết
| Bài tập 1: Gọi $M$ là điểm biểu diễn của số phức $z$ thỏa mãn $3\left| z+i \right|=\left| 2\overline{z}-z+3i \right|$. Tập hợp tất cả các điểm $M$ như vậy là:
A. một đường tròn B. một parabol C. một đường thẳng D. một elip |
Lời giải chi tiết
Gọi $z=x+yi\left( x;y\in \mathbb{R} \right)$ khi đó ta có: $3\left| x+yi+i \right|=\left| 2\left( x-yi \right)-\left( x+yi \right)+3i \right|$
$\Leftrightarrow 3\left| x+\left( y+1 \right)i \right|=\left| x-\left( 3y-3 \right)i \right|\Leftrightarrow 9{{x}^{2}}+9{{\left( y+1 \right)}^{2}}={{x}^{2}}+9{{\left( y-1 \right)}^{2}}$
$\Leftrightarrow 8{{x}^{2}}+18y=0\Leftrightarrow y=-\frac{4}{9}{{x}^{2}}$ nên tập hợp là Parabol. Chọn B.
| Bài tập 2: Tìm tập hợp các điểm biểu diễn số phức $z$ sao cho $\left( z-1 \right)\left( \overline{z}+1 \right)$ là số thực.
A. một đường tròn B. một parabol C. một đường thẳng D. một elip |
Lời giải chi tiết
Đặt $z=x+yi$ ta có: $\left( z-1 \right)\left( \overline{z}+1 \right)=\left( x+yi-1 \right)\left( x-yi+1 \right)=\left[ \left( x-1 \right)+yi \right]\left[ \left( x+1 \right)-yi \right]$
$=\left( x-1 \right)\left( x+1 \right)+{{y}^{2}}+\left[ \left( x-1 \right)\left( -y \right)+y\left( x+1 \right) \right]i$ là số thực nên ta có: $-xy+y+xy+y=0$
$\Leftrightarrow y=0$. Vậy điểm biểu diễn số phức $z$ là đường thẳng $y=0$. Chọn C.
| Bài tập 3: Gọi $M$ là điểm biểu diễn của số phức $z$ thỏa mãn $2\left| z-i \right|=\left| z-\overline{z}+2i \right|$. Tập hợp tất cả các điểm $M$ như vậy là:
A. một đường tròn B. một parabol C. một đường thẳng D. một elip |
Lời giải chi tiết
Đặt $z=x+yi\left( x;y\in \mathbb{R} \right)\Rightarrow \overline{z}=x-yi$
Ta có: $2\left| z-i \right|=\left| z-\overline{z}+2i \right|\Leftrightarrow 2\left| x+\left( y-1 \right)i \right|=\left| 2yi+2i \right|\Leftrightarrow {{x}^{2}}+{{\left( y-1 \right)}^{2}}={{\left( y+1 \right)}^{2}}\Leftrightarrow y=\frac{{{x}^{2}}}{4}$
Tập hợp điểm biểu diễn $z$ là parabol $y=\frac{{{x}^{2}}}{4}$. Chọn B.
| Bài tập 4: Gọi $M$ là điểm biểu diễn của số phức $z$ thỏa mãn $\left| z-i \right|=\left| \left( 1+i \right)z \right|$. Tập hợp tất cả các điểm $M$ như vậy là đường tròn có bán kính
A. $R=2$ B. $R=\sqrt{2}$ C. $R=4$ D. $R=1$ |
Lời giải chi tiết
Đặt $z=x+yi\left( x;y\in \mathbb{R} \right)$. Ta có: $\left| z-i \right|=\left| \left( 1+i \right)z \right|\Rightarrow \left| z-i \right|=\left| \left( 1+i \right) \right|\left| z \right|=\sqrt{2}\left| z \right|$
$\Rightarrow \left| x+yi-i \right|=\sqrt{2}\sqrt{{{x}^{2}}+{{y}^{2}}}\Leftrightarrow {{x}^{2}}+{{\left( y-1 \right)}^{2}}=2{{x}^{2}}+2{{y}^{2}}$
$\Leftrightarrow {{x}^{2}}+{{\left( y-1 \right)}^{2}}=2\Rightarrow $ Tập hợp điểm $M$ là đường tròn có bán kính $R=\sqrt{2}$. Chọn B.
| Bài tập 5: Biết điểm biểu diễn số phức $z$ thỏa mãn $\left( z+2i \right)\left( \overline{z}-1 \right)$ là số thực là một đường thẳng, khoảng cách từ gốc tọa độ đến đường thẳng đó bằng
A. $d=2$ B. $d=\frac{2}{\sqrt{5}}$ C. $d=\sqrt{2}$ D. $d=\frac{4}{\sqrt{5}}$ |
Lời giải chi tiết
Đặt $z=x+yi\left( x;y\in \mathbb{R} \right)$ ta có: $\left[ x+\left( y+2 \right)i \right]\left[ \left( x-1 \right)-yi \right]$ là số thực $\Rightarrow \left( x-1 \right)\left( y+2 \right)-xy=0$
$\Leftrightarrow xy-y+2x-2-xy=0\Leftrightarrow 2x-y-2=0$
Vậy tập hợp các điểm biểu diễn $z$ là đường thẳng $2x-y-2=0\left( \Delta \right)\Rightarrow d\left( O;\Delta \right)=\frac{2}{\sqrt{5}}$. Chọn B.
| Bài tập 6: Trong mặt phẳng tọa độ $Oxy$, tập hợp điểm biểu diễn các số phức $z$ thỏa mãn điều kiện $\left| zi-\left( 2+i \right) \right|=2$ là đường tròn
A. ${{\left( x-1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=4$ B. ${{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}=4$ C. ${{\left( x+1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=4$ D. ${{\left( x+1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}=4$ |
Lời giải chi tiết
Ta có: $\left| zi-\left( 2+i \right) \right|=2\Leftrightarrow \left| i \right|.\left| z-\frac{2+i}{i} \right|=2\Leftrightarrow \left| z-1+2i \right|=2$
Do đó tập hợp điểm biểu diễn $z$ là đường tròn ${{\left( x-1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=4$. Chọn A.
| Bài tập 7: [Đề thi THPT Quốc gia năm 2018] Xét các số phức $z$ thỏa mãn $\left( \overline{z}+i \right)\left( z+2 \right)$ là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn số phức $z$ là một đường tròn có bán kính bằng
A. 1 B. $\frac{5}{4},$ C. $\frac{\sqrt{5}}{2}$ D. $\frac{\sqrt{3}}{2}$ |
Lời giải chi tiết
Đặt $z=x+yi\left( x;y\in \mathbb{R} \right)$ ta có: $w=\left( \overline{z}+i \right)\left( z+2 \right)=\left( x-yi+i \right)\left( x+yi+2 \right)$
$=\left[ x+\left( 1-y \right)i \right]\left[ \left( x+2 \right)+yi \right]$
Phần thực của số phức $w$ là: ${{x}^{2}}-\left( 1-y \right)y$
Do $w$ là số thuần ảo nên phần thực của nó bằng 0 suy ra
$x\left( x+2 \right)-\left( 1-y \right)y={{x}^{2}}+{{y}^{2}}+2x-y=0\Leftrightarrow {{\left( x+1 \right)}^{2}}+{{\left( y-\frac{1}{2} \right)}^{2}}=\frac{5}{4}$
Do đó tập hợp điểm biểu diễn số phức $z$ là đường tròn tâm $I\left( -1;\frac{1}{2} \right)$ bán kính $R=\frac{\sqrt{5}}{2}$. Chọn C.
| Bài tập 8: [Đề minh họa BGD và ĐT 2017] Cho các số phức $z$ thỏa mãn $\left| z \right|=4$. Biết rằng tập hợp các điểm biểu diễn số phức $w=\left( 3+4i \right)z+i$ là một đường tròn. Tìm bán kính của đường tròn đó
A. $r=4$ B. $r=5$ C. $r=20$ D. $r=22$ |
Lời giải chi tiết
Ta có: $z=\frac{w-i}{3+4i}\Rightarrow \left| z \right|=\left| \frac{w-i}{3+4i} \right|=\frac{\left| w-i \right|}{5}=4\Leftrightarrow \left| w-i \right|=20$ $\Rightarrow $ tập hợp là đường tròn $I\left( 0;1 \right);\,\,r=20$. Chọn C.
| Bài tập 9: Cho các số phức $z$ thỏa mãn $\left| z \right|=2$ và số phức $w$ thỏa mãn $i.\overline{w}=\left( 3-4i \right)z+2i$. Biết rằng tập hợp điểm biểu diễn số phức $w$ là một đường tròn. Tính bán kính đường tròn đó:
A. $R=5$ B. $R=10$ C. $R=14$ D. $R=20$ |
Lời giải chi tiết
Ta có: $\left| i\overline{w}-2i \right|=\left| \left( 3-4i \right)z \right|=\left| \left( 3-4i \right) \right|\left| z \right|=5.2=10$
Do đó $\left| i \right|.\left| \overline{w}-2 \right|=10\Leftrightarrow \left| \overline{w}-2 \right|=10$, đặt $w=x+yi\left( x;y\in \mathbb{R} \right)$ thì $\left| x-yi-2 \right|=10$
$\Leftrightarrow {{\left( x-2 \right)}^{2}}+{{y}^{2}}=100\Rightarrow R=10$. Chọn C.
| Bài tập 10: Cho số phức $z$ thỏa mãn $\left| \frac{3-i}{1-2i}z+2 \right|=10$. Biết tập hợp các điểm biểu diễn số phức $w$ thỏa mãn $\left( 1+i \right)w-iz+1=0$ là một đường tròn. Tìm bán kính của đường tròn đó.
A. $R=5\sqrt{2}$ B. $R=5$ C. $R=10$ D. $R=50$ |
Lời giải chi tiết
Ta có: $\left| \frac{3-i}{1-2i}z+2 \right|=10\Leftrightarrow \left| \left( 1+i \right)z+2 \right|=10\Leftrightarrow \left| 1+i \right|\left| z+1-i \right|=10\Leftrightarrow \left| z+1-i \right|=5\sqrt{2}\,\,\,\,\,\left( 1 \right)$
Lại có: $z=\frac{\left( 1+i \right)w+1}{i}=\left( 1-i \right)w-i$ thế vào (1) ta được $\left| \left( 1+i \right)w+1-2i \right|=5\sqrt{2}\,$
$\Leftrightarrow \left| \left( 1-i \right) \right|\left| w-\frac{1}{2}+\frac{3}{2}i \right|=5\sqrt{2}\,\Leftrightarrow \left| w-\frac{1}{2}+\frac{3}{2}i \right|=5$. Do đó suy ra $R=5$. Chọn B.
| Bài tập 11: Cho số phức $z$ thỏa mãn $\left| 5z+i \right|=\left| 5-iz \right|$. Biết rằng tập hợp các điểm biểu diễn cho số phức $w$ thỏa mãn $w\left( 1-i \right)=\left( 6-8i \right)z+3i+2$ là một đường tròn. Xác định tọa độ tâm $I$ của đường tròn đó
A. $I\left( -1;5 \right)$ B. $I\left( 1;-5 \right)$ C. $I\left( \frac{1}{2};-\frac{5}{2} \right)$ D. $I\left( -\frac{1}{2};\frac{5}{2} \right)$ |
Lời giải chi tiết
Ta có: $\left| 5z+i \right|=\left| 5-iz \right|\Leftrightarrow \left| 5x+\left( 5y+1 \right)i \right|=\left| 5-xi+y \right|\Leftrightarrow 25{{x}^{2}}+{{\left( 5y+1 \right)}^{2}}={{x}^{2}}+{{\left( y+5 \right)}^{2}}$
$\Leftrightarrow 24\left( {{x}^{2}}+{{y}^{2}} \right)=24\Leftrightarrow {{x}^{2}}+{{y}^{2}}=1\Leftrightarrow \left| z \right|=1$
Khi đó $w\left( 1-i \right)=\left( 6-8i \right)z+3i+2\Leftrightarrow w\left( 1-i \right)-3i-2=\left( 6-8i \right)z$
Lấy modun 2 vế ta được $\left| w\left( 1-i \right)-3i-2 \right|=10\Leftrightarrow \left| 1-i \right|\left| w-\frac{3i+2}{i-1} \right|=10$
$\Leftrightarrow \left| w-\left( \frac{-1}{2}+\frac{5}{2} \right)i \right|=5\sqrt{2}$. Do đó tập hợp điểm biểu diễn $z$ là đường tròn tâm $I\left( -\frac{1}{2};\frac{5}{2} \right);R=5\sqrt{2}$ Chọn D.
| Bài tập 12: Cho số phức $z$ thỏa mãn $\left| \frac{3+i}{1-i}z+4+3i \right|=\sqrt{5}$. Biết rằng tập hợp các điểm biểu diễn số phức $w$ thỏa mãn $w=\left( 3+4i \right)z+2i$ là một đường tròn. Phương trình đường tròn đó là:
A. ${{\left( x+10 \right)}^{2}}+{{\left( y+3 \right)}^{2}}=5$ B. ${{\left( x+10 \right)}^{2}}+{{\left( y+3 \right)}^{2}}=25$ C. ${{\left( x-10 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=5$ D. ${{\left( x-10 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=25$ |
Lời giải chi tiết
Ta có: $\left| \frac{3+i}{1-i}z+4+3i \right|=\sqrt{5}\Leftrightarrow \left| \left( 1+2i \right)z+4+3i \right|=\sqrt{5}\Leftrightarrow \left| 1+2i \right|\left| z+2-i \right|=\sqrt{5}\Leftrightarrow \left| z+2-i \right|=1$
Mặt khác $z=\frac{w-2i}{3+4i}$ suy ra $\left| \frac{w-2i}{3+4i}+2-i \right|=1\Leftrightarrow \frac{\left| w+10+3i \right|}{\left| 3+4i \right|}=1\Leftrightarrow \left| w+10+3i \right|=5$
Do đó phương trình đường tròn biểu diễn $w$ là ${{\left( x+10 \right)}^{2}}+{{\left( y+3 \right)}^{2}}=25$. Chọn B.
| Bài tập 13: Tập hợp điểm biểu diễn số phức $w=2z+3-i$, biết ${{\left| 2z+i \right|}^{2}}=3z.\overline{z}+1$ là đường tròn có tâm
A. $I\left( 3;5 \right)$ B. $I\left( -3;5 \right)$ C. $I\left( -3;-1 \right)$ D. $I\left( 3;-5 \right)$ |
Lời giải chi tiết
Đặt $w=x+yi\left( x,y\in \mathbb{R} \right),\,\,z=a+bi\left( a,b\in \mathbb{R} \right)$. Ta có: $x+yi=2\left( a+bi \right)+3-i\Leftrightarrow \left\{ \begin{align} & x=2a+3 \\ & y=2b-1 \\ \end{align} \right.$
Ta có: ${{\left| 2z+i \right|}^{2}}=3z.\overline{z}+1\Leftrightarrow {{\left| 2a+\left( 2b+1 \right) \right|}^{2}}=3\left( {{a}^{2}}+{{b}^{2}} \right)+1\Leftrightarrow 4{{a}^{2}}+{{\left( 2b+1 \right)}^{2}}=3{{a}^{2}}+3{{b}^{2}}+1$
$\Leftrightarrow {{a}^{2}}+{{b}^{2}}+4b=0\Leftrightarrow {{a}^{2}}+{{\left( b+2 \right)}^{2}}=4\Leftrightarrow {{\left( \frac{x-3}{2} \right)}^{2}}+{{\left( \frac{y+1}{2}+2 \right)}^{2}}=4\Leftrightarrow {{\left( x-3 \right)}^{2}}+{{\left( y+5 \right)}^{2}}=16$
Vậy tập hợp các điểm biểu diễn $w$ là đường tròn tâm $I\left( 3;-5 \right)$, bán kính $R=4$. Chọn D.
| Bài tập 14: Tập hợp các điểm biểu diễn số phức $w=\left( 1+2i \right)z$ biết rằng số phức $z$ thỏa mãn điều kiện ${{\left| z+2-i \right|}^{2}}=z\overline{z}$ là đường thẳng $d$. Khoảng cách từ $O$ đến $d$ bằng
A. $\frac{5}{4}$ B. $\frac{5}{2}$ C. $\frac{25}{4}$ D. $\frac{25}{2}$ |
Lời giải chi tiết
Đặt $w=x+yi$ và $z=a+bi\left( a;b;x;y\in \mathbb{R} \right)$ ta có: $x+yi=\left( 1+2i \right)\left( a+bi \right)=a-2b+\left( 2a+b \right)i$
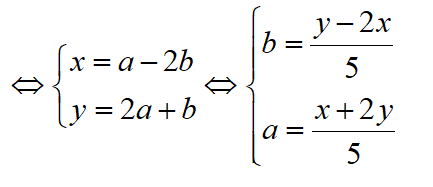
Mặt khác ${{\left| z+2-i \right|}^{2}}=z\overline{z}\Leftrightarrow {{\left( a+2 \right)}^{2}}+{{\left( b-1 \right)}^{2}}=\left( {{a}^{2}}+{{b}^{2}} \right)\Leftrightarrow 4a-2b+5=0$
$\Leftrightarrow \frac{4x+8y}{5}-\frac{2y-4x}{5}+5=0\Leftrightarrow 8x+6y+25=0$
Vậy tập hợp điểm biểu diễn số phức $w$ là đường thẳng $\left( d \right):8x+6y+25=0$
Do đó $d\left( O;d \right)=\frac{25}{10}=\frac{5}{2}$. Chọn B.
| Bài tập 15: Cho các số phức $z$ thỏa mãn $\left| z-i \right|=\left| z-1+2i \right|$. Tập hợp các điểm biểu diễn số phức $w=\left( 2-i \right)z+1$ trên mặt phẳng tọa độ là một đường thẳng. Diện tích tam giác tạo bởi đường thẳng đó với các trục tọa độ bằng
A. $\frac{81}{7}$ B. $\frac{9}{7}$ C. $\frac{9}{14}$ D. $\frac{81}{14}$ |
Lời giải chi tiết
Ta có: $w=\left( 2-i \right)z+1\Rightarrow z=\frac{w-1}{2-i}$
Do đó $\left| z-i \right|=\left| z-1+2i \right|\Leftrightarrow \left| \frac{w-1}{2-i}-i \right|=\left| \frac{w-1}{2-i}-1+2i \right|\Leftrightarrow \left| \text{w}-1-i(2-i) \right|=\left| w-1+\left( 2i-1 \right)\left( 2-i \right) \right|$
$\Leftrightarrow \left| w-2-2i \right|=\left| w-1+5i \right|$
Do đó tập hợp điểm biểu diễn của $w$ là trung trực $d$ của $AB$ với $A\left( 2;2 \right);\,\,B\left( 1;-5 \right)$
Ta có: trung điểm của $AB$ là $\left( \frac{3}{2};-\frac{3}{2} \right);\,\,\overrightarrow{n}=\overrightarrow{AB}=\left( 1;7 \right)\Rightarrow d:x+7y+9=0$
Khi đó $d$ cắt các trục tọa độ tại $M\left( 0;\frac{-9}{7} \right);\,N\left( -9;0 \right)\Rightarrow {{S}_{OMN}}=\frac{1}{2}OM.ON=\frac{81}{14}$. Chọn D.
| Bài tập 16: Biết tập hợp các điểm $M$ biểu diễn hình học số phức $z$ thỏa $\left| z+4 \right|+\left| z-4 \right|=10$ là một Elip $\left( E \right)$. Phương trình Elip $\left( E \right)$ là:
A. $\frac{{{x}^{2}}}{5}+\frac{{{y}^{2}}}{3}=1$ B. $\frac{{{x}^{2}}}{25}+\frac{{{y}^{2}}}{16}=1$ C. $\frac{{{x}^{2}}}{25}+\frac{{{y}^{2}}}{9}=1$ D. $\frac{{{x}^{2}}}{16}+\frac{{{y}^{2}}}{9}=1$ |
Lời giải chi tiết
Gọi ${{F}_{1}}\left( -4;0 \right);\,\,{{F}_{2}}\left( 4;0 \right)$ và lần lượt là các điểm biểu diễn số phức $-4;4$ và $z$
Ta có: $\left| z+4 \right|+\left| z-4 \right|=10\Leftrightarrow M{{F}_{1}}+M{{F}_{2}}=10>{{F}_{1}}{{F}_{2}}=8$
Khi đó tập hợp điểm $M$ là Elip có $2a=10;2c=8\Rightarrow \left\{ \begin{align} & a=5 \\ & c=4 \\ & b=\sqrt{{{a}^{2}}-{{b}^{2}}}=3 \\ \end{align} \right.$
Phương trình Elip là: $\frac{{{x}^{2}}}{25}+\frac{{{y}^{2}}}{9}=1$. Chọn C.
| Bài tập 17: Trên mặt phẳng phức, gọi $M$ là điểm biểu diễn số phức $z={{\left( 2+i \right)}^{2}}\left( 4-i \right)$ và gọi $\varphi $ là góc tạo bởi chiều dương trục hoành và véc-tơ $\overrightarrow{OM}$. Tính $\cos 2\varphi $.
A. $\cos 2\varphi =-\frac{87}{475}$ B. $\cos 2\varphi =\frac{87}{475}$ C. $\cos 2\varphi =-\frac{87}{425}$ D. $\cos 2\varphi =\frac{87}{425}$ |
Lời giải chi tiết
Ta có $z=16+13i\Rightarrow M\left( 16;13 \right)$ và nằm ở góc phần tư thứ nhất nên ta có
$\cos \varphi =\cos \left( \overrightarrow{OM};\overrightarrow{i} \right)=\frac{16}{\sqrt{{{16}^{2}}+{{13}^{2}}}}=\frac{16}{\sqrt{425}}\Rightarrow \cos 2\varphi =2{{\cos }^{2}}\varphi -1=\frac{87}{425}$. Chọn D.
| Bài tập 18: Trên mặt phẳng tọa độ $Oxy$, lấy $M$ là điểm biểu diễn số phức $z=-1+2i$ và gọi $\varphi $ là góc lượng giác tia đầu $Ox$, tia cuối $OM$. Tính $\tan 2\varphi $.
A. $\tan 2\varphi =-\frac{4}{3}$ B. $\tan 2\varphi =-\frac{3}{4}$ C. $\tan 2\varphi =\frac{4}{3}$ D. $\tan 2\varphi =-1$ |
Lời giải chi tiết
Ta có $z=-1+2i\Rightarrow M\left( -1;2 \right)$ và nằm ở góc phần tư thứ III nên ta có
$\cos \varphi =\cos \left( \overrightarrow{OM};\overrightarrow{i} \right)=\frac{-1}{\sqrt{{{\left( -1 \right)}^{2}}+{{2}^{2}}}}=-\frac{1}{\sqrt{5}}\Rightarrow \tan 2\varphi =\frac{\sin 2\varphi }{\cos 2\varphi }=\frac{4}{3}$. Chọn C.
| Bài tập 19: Cho hai số phức ${{z}_{1}},\,\,{{z}_{2}}$ thỏa mãn $\left| {{z}_{1}} \right|=2,\,\,\left| {{z}_{2}} \right|=\sqrt{3}$ và nếu gọi $M,\,\,N$ lần lượt là điểm biểu diễn của ${{z}_{1}},\,\,i{{z}_{2}}$ thì $\widehat{MON}=30{}^\circ $, Tính $P=\left| z_{1}^{2}+4z_{2}^{2} \right|$.
A. $P=\sqrt{5}$ B. $P=4\sqrt{7}$ C. $P=3\sqrt{3}$ D. $P=5\sqrt{2}$ |
Lời giải chi tiết
Ta có $P=\left| z_{1}^{2}-4{{\left( i{{z}_{2}} \right)}^{2}} \right|=\left| {{a}^{2}}-4{{b}^{2}} \right|=\left| a-2b \right|.\left| a+2b \right|$. Với $a={{z}_{1}}\Rightarrow \left| a \right|=2;\,\,b=i{{z}_{2}}\Rightarrow \left| b \right|=\sqrt{3}$
Lại có ${{\left| a-2b \right|}^{2}}={{\left| a \right|}^{2}}-4.\left| a \right|.\left| b \right|.cos30{}^\circ +4{{\left| b \right|}^{2}}=4\xrightarrow{{}}\left| a-2b \right|=2$
Và ${{\left| a+2b \right|}^{2}}={{\left| a \right|}^{2}}+4.\left| a \right|.\left| b \right|.cos30{}^\circ +4{{\left| b \right|}^{2}}=28\xrightarrow{{}}\left| a+2b \right|=2\sqrt{7}$
Vậy $P=\left| a-2b \right|.\left| a+2b \right|=2.2\sqrt{7}=4\sqrt{7}$. Chọn B.
