Vecto trong không gian là gì? Vecto chỉ phương, tích vô hướng, quy tắc – lý thuyết Vecto
Định nghĩa: Veto trong không gian là gì?
Vectơ trong không gian là một đoạn thằng có hướng. Kí hiệu $\overrightarrow{AB}$ chỉ vectơ có điểm đầu A, điểm cuối B. Vectơ còn được kí hiệu là $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$,…
Các quy tắc về vectơ:
Quy tắc 3 điểm: $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}$ hoặc $\overrightarrow{AC}=\overrightarrow{BC}-\overrightarrow{BA}$
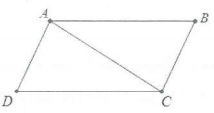
Quy tắc hình bình hành: Cho hình bình hành ACBD ta có: $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$
Quy tắc trung điểm: Nếu M là trung điểm của AB thì $\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}$
![]()
Quy tắc trung tuyến: Nếu AP là trung tuyến của tam giác ABC thì $\overrightarrow{AP}=\frac{1}{2}\left( \overrightarrow{AB}+\overrightarrow{AC} \right)$
Tương tự hình bên ta có: $\left\{ \begin{array} {} \overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BN} \\ {} \overrightarrow{CB}+\overrightarrow{CA}=2\overrightarrow{CM} \\ \end{array} \right.$
Quy tắc trọng tâm: Nếu G là trọng tâm tam giác ABC thì $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$
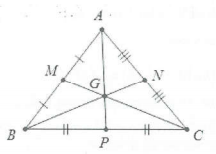
Khi đó với mọi điểm M ta có: $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$
Quy tắc hình hộp: Cho hình hộp ABCD.A’B’C’D’ thì $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA’}=\overrightarrow{AC’}$
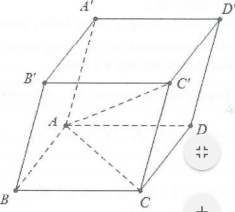
Chứng minh:
Ta có: ACC’A’ là hình bình hành nên $\overrightarrow{AC’}=\overrightarrow{AC}+\overrightarrow{AA’}$
Tương tự: $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$ suy ra $\overrightarrow{AC’}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA’}$
Chú ý: Nếu G là trong tâm tứ diện ABCD, ta có: $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$
Sự đồng phẳng của các vectơ, điều kiện để va vectơ đồng phẳng
Định nghĩa: Ba vectơ gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng.
Điều kiện để ba vectơ đồng phẳng:
Định lí 1: Điều kiện cần và đủ để ba vectơ $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$ đồng phẳng là $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng phương hoặc tồn tại các số m, n duy nhất sao cho $\overrightarrow{c}=m.\overrightarrow{a}+n.\overrightarrow{b}$
Định lí 2: Nếu $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$ là ba vectơ không đồng phẳng thì với mỗi vectơ $\overrightarrow{d}$ trong không gian, ta tìm được các số m, n, p duy nhất sao cho
Tích vô hướng của 2 vectơ
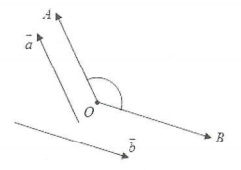
Góc giữa 2 vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ khác $\overrightarrow{0}$ được định nghĩa bằng góc AOB với $\overrightarrow{OA}=\overrightarrow{a}$; $\overrightarrow{OB}=\overrightarrow{b}$
Nếu $\overrightarrow{a}$ hoặc $\overrightarrow{b}$ bằng $\overrightarrow{0}$ ta quy ước góc giữa chúng có thể nhận một giá trị tùy ý.
Tích vô hướng giữa 2 vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ là một số, được kí hiệu $\overrightarrow{a}.\overrightarrow{b}$ và được xác định bởi $\overrightarrow{a}.\overrightarrow{b}=\left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right|\cos \left( \overrightarrow{a};\overrightarrow{b} \right)$ từ đó suy ra cosin góc giữa 2 vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ là $\cos \left( \overrightarrow{a};\overrightarrow{b} \right)=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right|}$
Đặc biệt khi $\overrightarrow{a}\bot \overrightarrow{b}\Leftrightarrow \cos \left( \overrightarrow{a};\overrightarrow{b} \right)=0\Leftrightarrow \overrightarrow{a}.\overrightarrow{b}=0$
Tính chất: Cho 3 vectơ $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$ và số thực k. Khi đó ta có:
| i) $\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{a}$ | ii) $\overrightarrow{a}\left( \overrightarrow{b}+\overrightarrow{c} \right)=\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{a}.\overrightarrow{c}$ |
| iii) $\left( k\overrightarrow{a} \right)\overrightarrow{b}=k\left( \overrightarrow{a}.\overrightarrow{b} \right)+\overrightarrow{a}.\left( k\overrightarrow{b} \right)$ | iv) ${{\left| \overrightarrow{a} \right|}^{2}}={{\overrightarrow{a}}^{2}}$ |
Vectơ chỉ phương của đường thằng:
Vectơ $\overrightarrow{a}\ne \overrightarrow{0}$ được gọi là vectơ chỉ phương của đường thằng d nếu giá của vectơ $\overrightarrow{a}$ song song hoặc trùng với đường thẳng d
Một đường thẳng d trong không gian hoàn toàn xác định nếu biết một điểm A thuộc d và một vectơ chỉ phương $\overrightarrow{a}$ của đường thẳng d.
Ứng dụng của tích vô hướng
Tính độ dài đoạn thẳng AB: $AB=\left| \overrightarrow{AB} \right|=\sqrt{{{\overrightarrow{AB}}^{2}}}$
Xác định góc giữa hai vectơ: $\cos \left( \overrightarrow{a};\overrightarrow{b} \right)=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right|}$