Hai mặt phẳng song song khi nào? Bài tập và cách chứng minh
Phương pháp chứng minh hai mặt phẳng song song với nhau
■ Định nghĩa: Hai mặt phẳng được gọi là song song nếu chúng không có điểm chung.
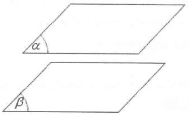
■ Định lý: Nếu mặt phẳng $\left( \alpha \right)$ chứa hai đường thẳng a và b cắt nhau và cùng song song với $\left( \beta \right)$ thì $\left( \alpha \right)$song song với $\left( \beta \right)$.
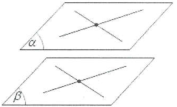
■ Tính chất 1: Qua một điểm A nằm ngoài mặt phẳng $\left( \beta \right)$ cho trước, có duy nhất một mặt phẳng $\left( \alpha \right)$ song song với $\left( \beta \right)$.
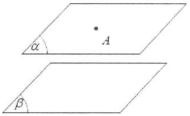
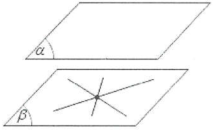
$\Rightarrow $ Hệ quả: Cho điểm A không nằm trên mặt phẳng $\left( \alpha \right)$. Khi đó các đường thẳng đi qua A và song song với $\left( \alpha \right)$ cùng nằm trên mặt phẳng $\left( \beta \right)$ đi qua A và song song với $\left( \alpha \right)$.
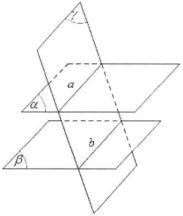
■ Tính chất 2: Cho hai mặt phắng $\left( \alpha \right)$ và $\left( \beta \right)$ song song với nhau. Khi đó một mặt phẳng nếu cắt $\left( \alpha \right)$ và $\left( \beta \right)$ lần lượt theo các giao tuyến a, b thì a song song với b.
Phương pháp giải toán:
Để chứng minh hai mặt phẳng (P) và (Q) song song với nhau ta chứng minh hai đường thẳng a và b cắt nhau nằm trong mặt phẳng (P) song song với lần lượt hai đường thẳng ${a}’$ và ${b}’$ cắt nhau nằm trong mặt phẳng (Q).
Bài tập chứng minh hai mặt phẳng song song có đáp án chi tiết
| Bài tập 1: Cho hình chóp S.ABCD, có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA, SD.
a) Chứng minh $\left( OMN \right)//\left( SBC \right).$ b) Gọi P, Q lần lượt là trung điểm của AB, ON. Chứng minh $PQ//\left( SBC \right).$ |
Lời giải chi tiết
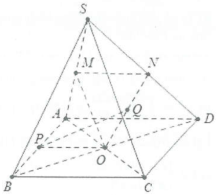
a) Ta có MO là đường trung bình trong tam giác $SAC\Rightarrow MO//AC.$
Mặt khác N và O lần lượt là trung điểm của SD và BD nên NO là đường trung bình trong $\Delta SBD\Rightarrow NO//SB.$
Ta có: $\left\{ \begin{array} {} MO//SC \\ {} NO//SB \\ {} MO\cap NO=O \\ {} SC\cap SB=S\text{ } \\ \end{array} \right.\Rightarrow \left( OMN \right)//\left( SBC \right).$
b) Do P và O lần lượt là trung điểm của AB và AC nên $OP//AD//BC\Rightarrow OP//\left( SBC \right).$
Lại có $ON//SB\Rightarrow OQ//\left( SBC \right).$
Do vậy $\left( OPQ \right)//\left( SBC \right)\Rightarrow PQ//\left( SBC \right).$
| Bài tập 2: Cho hình chóp S.ABCD, có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA và CD.
a) Chứng minh rằng $\left( OMN \right)//\left( SBC \right).$ b) Gọi I là trung điểm của SD, J là một điểm trên (ABCD) và cách đều AB, CD. Chứng minh rằng $IJ//\left( SAB \right).$ |
Lời giải chi tiết
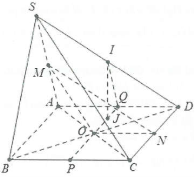
a) Ta có N và O lần lượt là trung điểm của CD và AC nên NO là đường trung bình trong $\Delta BCD\Rightarrow NO//BC$.
Tương tự MO là đường trung bình trong tam giác SAC nên $MO//SC$.
Lại có: $\left\{ \begin{array} {} NO//BC \\ {} MO//SC \\ {} OM\cap ON=O \\ {} BC\cap SC=S\text{ } \\ \end{array} \right.\Rightarrow \left( OMN \right)//\left( SBC \right)$
b) Ta có P và Q lần lượt là trung điểm của BC và AD thì PQ là đường thẳng cách đều AB và CD do vậy điểm $J\in PQ$. Do IQ là đường trung bình của $\Delta SAD$ nên $IQ//SA$.
Ta có: $PQ//\left( SAB \right);IQ//\left( SAB \right)\Rightarrow \left( IPQ \right)//\left( SAB \right)$
Mặt khác $IJ\subset \left( IPQ \right)\Rightarrow IJ//\left( SAB \right).$
| Bài tập 3: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N, P, Q là trung điểm của BC, AB, SB và AD.
a) Chứng minh rằng: $\left( MNP \right)//\left( SAC \right).$ b) Chứng mình rằng: $PQ//\left( SCD \right).$ c) Gọi I là giao điểm của AM và BD; J là điểm thuộc SA sao cho $AJ=2JS.$ Chứng minh $IJ//\left( SBC \right).$ |
Lời giải chi tiết
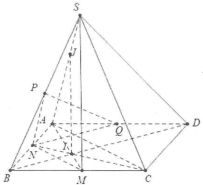
a) Ta có PN là đường trung bình trong $\Delta SAB$
Suy ra $PN//SA.$
Tương tự ta có: $MP//SC\Rightarrow \left( MNP \right)//\left( SAC \right).$
(hai mặt phẳng có cặp cạnh song song cắt nhau).
b) Ta có: $\left\{ \begin{array} {} MQ//CD \\ {} MP//SC \\ \end{array} \right.\Rightarrow \left( MPQ \right)//\left( SCD \right)$
Lại có $PQ\subset \left( MNQ \right)\Rightarrow PQ//\left( SCD \right).$
c) Do $\left\{ \begin{array} {} I=AM\cap BD \\ {} BM//AD \\ \end{array} \right.$
Theo định lý Talet ta có: $\frac{MI}{IA}=\frac{BM}{AD}=\frac{1}{2}$
Mặt khác: $\frac{SJ}{JA}=\frac{1}{2}\Rightarrow \frac{MI}{IA}=\frac{SJ}{JA}\Rightarrow \text{IJ}//SM.$
Do $SM\subset \left( SBC \right)$ suy ra $\text{IJ}//\left( SBC \right).$
| Bài tập 4: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N là trung điểm của SA, CD.
a) Chứng minh rằng $\left( OMN \right)//\left( SBC \right).$ b) Tìm giao điểm I của ON và (SAB). c) Gọi $G=SI\cap BM$, H là trọng tâm của $\Delta SCD$. Chứng minh rằng $GH//\left( SAD \right).$ d) Gọi J là trung điểm AD, $E\in MJ$. Chứng minh rằng $OE//\left( SCD \right)$. |
Lời giải chi tiết
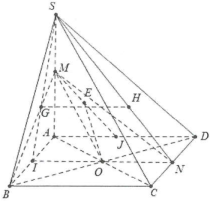
a) Ta có: OM là đường trung bình trong tam giác SAC suy ra $OM//SC.$
Lại có: ON là đường trung bình trong tam giác BCD nên $ON//BC.$
Do vậy $\left( OMN \right)//\left( SBC \right).$
b) Trong mặt phẳng (ABCD), gọi $I=ON\cap AB$ khi đó I chính là giao điểm của ON và (SAB).
c) Dễ thấy G, H lần lượt là trọng tâm tam giác SAB và SCD do đó $\frac{SG}{SI}=\frac{SH}{SN}=\frac{2}{3}$
$\Rightarrow GH//IN//AD\Rightarrow GH//\left( SAD \right).$
d) Do O và J lần lượt là trung điểm của AC và AD nên $OJ//CD$ (tính chất đường trung bình).
Mặt khác O và M lần lượt là trung điểm của AC và SA nên $OM//SC.$
Do vậy $\left( OMJ \right)//\left( SCD \right)\Rightarrow OE//\left( SCD \right).$
| Bài tập 5: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SB, SC; lấy điểm $P\in SA.$
a) Tìm giao tuyến (SAB) và (SCD). b) Tìm giao điểm SD và (MNP). c) Tìm thiết diện hình chóp và mặt phẳng (MNP). Thiết diện là hình gì? d) Gọi $J\in MN$. Chứng minh rằng $OJ//\left( SAD \right).$ |
Lời giải chi tiết
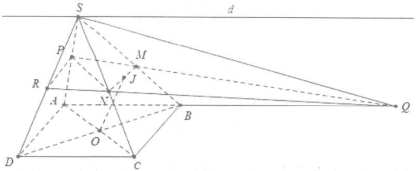
a) Do AB song song với CD nên giao tuyến của (SAB) và (SCD) là đường thẳng d đi qua S và song song với AB và CD.
b) Trong mặt phẳng (SAB), kéo dài PM cắt AB tại Q, trong mặt phẳng (PMQR), kéo dài QN cắt SD tại R, giao điểm của SD và (MNP) là R.
c) Thiết diện hình chóp và mặt phẳng (MNP) là tứ giác MPRN.
Do 3 mặt phẳng (MNP); (ABC); (SAD) cắt nhau theo 3 giao tuyến là PR; MN;AD nên chúng song song hoặc đồng quy.
Mặt khác $MN//AD\Rightarrow MN//AD//PR\Rightarrow $ MPRN là hình thang.
d) Ta có: OM là đường trung bình trong tam giác $SBD\Rightarrow OM//SD.$
Tương tự ta có: $ON//SA\Rightarrow \left( OMN \right)//\left( SAD \right).$
Mặt khác $OJ\subset \left( OMN \right)\Rightarrow OJ//\left( SAD \right)$ (điều phải chứng minh).
| Bài tập 6: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I, J, G, P, Q là trung điểm của DC, AB, SB, BG, BI.
a) Chứng minh rằng $\left( IJG \right)//\left( SAD \right).$ b) Chứng minh rằng $PQ//\left( SAD \right).$ c) Tìm giao tuyến của hai mặt phẳng (SAC) và (IJG). d) Tìm giao tuyến của hai mặt phẳng (ACG) và (SAD). |
Lời giải chi tiết
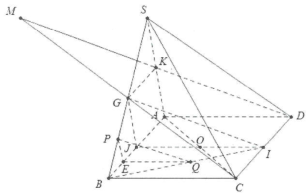
a) Ta có IJ là đường trung bình của hình bình hành ABCD nên $IJ//AD\left( l \right).$
Lại có JG là đường trung bình tam giác $SAB\Rightarrow JG//SA\left( 2 \right).$
Từ (l) và (2) suy ra $\left( IJG \right)//\left( SAD \right).$
b) Gọi E là trung điểm của JB thì $\frac{BE}{BA}=\frac{BP}{BS}=\frac{1}{4}\Rightarrow \text{EP}//AS.$
Mặt khác EQ là đường trung bình cùa tam giác BIJ nên $EQ//IJ\Rightarrow EQ//AD.$
Ta có: $\left\{ \begin{array} {} EP//SA \\ {} EQ//AD \\ \end{array} \right.\Rightarrow \left( EPQ \right)//\left( SAD \right).$
c) Trong mặt phẳng (ABC) gọi $O=IJ\cap AC.$
Ta có: $SA//JG$ nên giao tuyến của hai mặt phẳng (SAC) và (IJG) song song với SA
Khi đó giao tuyến của hai mặt phẳng (SAC) và (IJG) là đường thẳng đi qua O và song song với SA.
d) Gọi K là trung điểm của SA thì $GK//AB$ (tính chất đường trung bình)
Suy ra $GK//CD\Rightarrow G,K,C,D$ đồng phẳng.
Trong mặt phẳng (GKCD) gọi $M=DK\cap CG\Rightarrow \left\{ \begin{array} {} M\in \left( ACG \right) \\ {} M\in \left( SAD \right) \\ \end{array} \right..$
Do đó giao tuyến của hai mặt phẳng (ACG) và (SAD) là AM.
| Bài tập 7: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của BC, CD, SC.
a) Chứng minh rằng $\left( MNP \right)//\left( SBD \right).$ b) Tìm giao tuyến (SAB) và (SCD). c) Tìm giao tuyến của (MNP) và (SAD). Suy ra giao điểm của SA và (MNP). d) Gọi $I=AP\cap SO,\text{ }J=AM\cap BD$ Chứng minh rằng $IJ//\left( MNP \right).$ |
Lời giải chi tiết
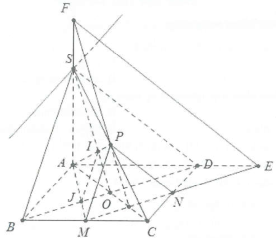
a) Ta có MN là đường trung bình trong tam giác BCD nên $MN//BD.$
Tương tự NP là đường trung bình trong tam giác SCD nên $NP//SD.$
Do vậy $\left( MNP \right)//\left( SBD \right).$
b) Do $AB//CD$ nên giao tuyến của (SAB) và (SCD) đi qua S và song song với AB và CD.
c) Gọi $E=MN\cap AD.$
Do $NP//SD$ nên giao tuyến $\Delta $ của (MNP) và (SAD) đi qua E và song song với SD.
Trong mặt phẳng (SAD) gọi $F=\Delta \cap SA\Rightarrow F=SA\cap \left( MNP \right).$
d) Ta có: $J=AM\cap BO;J=SO\cap AP$ do đó I, J lần lượt là trọng tâm tam giác SAC và ABC
Khi đó $\frac{AI}{AP}=\frac{\text{AJ}}{AM}=\frac{2}{3}\Rightarrow \text{IJ}//MP\Rightarrow IJ//\left( MNP \right).$
