Bài tập ứng dụng của tích phân tính thể tích khối tròn xoay có đáp án chi tiết
Bài tập trắc nghiệm ứng dụng tích phân tính thể tích khối tròn xoay có lời giải
| Ví dụ 1: Cho hình phẳng $\left( H \right)$ giới hạn bởi các đường $y={{x}^{2}};\,\,y=0;\,\,x=2$. Tính thể tích $V$ của khối tròn xoay thu được khi quay $\left( H \right)$ quanh trục $Ox.$
A. $V=\frac{8}{3}.$ B. $V=\frac{32}{5}.$ C. $V=\frac{8\pi }{3}.$ D. $V=\frac{32\pi }{5}.$ |
Lời giải:
Thể tích cần tính là $V=\pi \int\limits_{0}^{2}{{{x}^{4}}dx}=\pi .\left. \frac{{{x}^{5}}}{5} \right|_{0}^{2}=\frac{32\pi }{5}.$ Chọn D.
| Ví dụ 2: Cho hình phẳng $D$ giới hạn bởi đường cong $y=\sqrt{{{x}^{2}}+1}$, trục hoành và các đường thẳng $x=0,\,\,x=1.$ Khối tròn xoay tạo thành khi quay $D$ quanh trục hoành có thể tích $V$ bằng bao nhiêu?
A. $V=\frac{4\pi }{3}.$ B. $V=2\pi .$ C. $V=\frac{4}{3}.$ D. $V=2.$ |
Lời giải:
Thể tích cần tính bằng $V=\pi \int\limits_{0}^{1}{{{\left( \sqrt{{{x}^{2}}+1} \right)}^{2}}}dx=\frac{4\pi }{3}.$ Chọn A.
| Ví dụ 3: Cho hình phẳng $D$ giới hạn bởi đường cong $y=\sqrt{2+\cos x}$, trục hoành và các đường thẳng $x=0;\,\,x=\frac{\pi }{2}$. Khối tròn xoay tạo thành khi quay $D$ quanh trục hoành có thể tích $V$ bằng:
A. $V=\left( \pi +1 \right)\pi .$ B. $V=\pi -1.$ C. $V=\pi +1.$ D. $V=\left( \pi -1 \right)\pi .$ |
Lời giải:
Thể tích cần tính bằng $V=\pi \int\limits_{0}^{\frac{\pi }{2}}{{{\left( \sqrt{2+\cos x} \right)}^{2}}}dx=\pi \int\limits_{0}^{\frac{\pi }{2}}{\left( 2+\cos x \right)}\,dx=\pi \left. \left( 2x+sinx \right) \right|_{0}^{\frac{\pi }{2}}=\left( \pi +1 \right)\pi .$ Chọn A.
| Ví dụ 4: Cho $\left( H \right)$ là hình phẳng giới hạn bởi đường cong $\left( C \right):y=-{{x}^{2}}+4x$ và đường thẳng $d:y=x.$ Tính thể tích $V$ của vật thể tròn xoay do hình phẳng $\left( H \right)$ quay xung quanh trục hoành.
A. $V=\frac{81\pi }{10}.$ B. $V=\frac{81\pi }{5}.$ C. $V=\frac{108\pi }{5}.$ D. $V=\frac{108\pi }{10}.$ |
Lời giải:
Phương trình hoành độ giao điểm là: $-{{x}^{2}}+4x=x\Leftrightarrow -{{x}^{2}}+3x=0\Leftrightarrow \left[ \begin{array} {} x=0 \\ {} x=3 \\ \end{array} \right.$
Thể tích cần tìm là: $V=\pi \int\limits_{0}^{3}{\left| {{\left( 4x-{{x}^{2}} \right)}^{2}}-{{x}^{2}} \right|dx}=\frac{108\pi }{5}.$ Chọn C.
| Ví dụ 5: Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các đường $y=x\sqrt{\ln \left( 1+{{x}^{3}} \right)};\,\,y=0;\,\,x=1$ khi xoay quanh trục $Ox.$
A. $V=\pi \left( \frac{2\ln 2}{3}-\frac{1}{3} \right).$ B. $V=\pi \left( \frac{\ln 2}{3}-\frac{1}{3} \right).$ C. $V={{\pi }^{2}}\left( \frac{2\ln 2}{3}-\frac{1}{3} \right).$ D. $V={{\pi }^{2}}\left( \frac{\ln 2}{3}-\frac{1}{3} \right).$ |
Lời giải:
Phương trình hoành độ giao điểm là: $x\sqrt{\ln \left( 1+{{x}^{3}} \right)}=0\Leftrightarrow x=0$
Gọi $V$ là thể tích khối tròn xoay cần tìm ta có: $V=\pi \int\limits_{0}^{1}{{{x}^{2}}\ln \left( 1+{{x}^{3}} \right)dx}$
Đặt $\left\{ \begin{array} {} u=\ln \left( 1+{{x}^{3}} \right) \\ {} dv={{x}^{2}}dx \\ \end{array} \right.\Rightarrow \left\{ \begin{array} {} du=\frac{3{{x}^{2}}}{1+{{x}^{3}}} \\ {} v=\frac{{{x}^{3}}+1}{3} \\ \end{array} \right.\Rightarrow V=\pi \left( \left. \frac{{{x}^{3}}+1}{3}\left. \ln \left( 1+{{x}^{3}} \right) \right| \right|_{0}^{1}-\int\limits_{0}^{1}{{{x}^{2}}dx} \right)$
$=\pi \left( \frac{2\ln 2}{3}-\frac{1}{3} \right)\,\,\,\left( vtt \right).$ Chọn A.
| Ví dụ 6: Thể tích $V$ của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường $y=0,\,\,y=x\sqrt{\ln \left( x+1 \right)};\,\,x=1$ xung quanh trục $Ox$ là
A. $V=\frac{5\pi }{6}.$ B. $V=\frac{\pi }{6}\left( 12\ln 2-5 \right).$ C. $V=\frac{5\pi }{18}.$ D. $V=\frac{\pi }{18}\left( 12\ln 2-5 \right).$ |
Lời giải:
Phương trình hoành độ giao điểm của $\left( C \right)$ và $Ox$ là $x\sqrt{\ln \left( x+1 \right)}=0\Leftrightarrow x=0$
Thể tích khối tròn xoay cần tính là$\pi \int\limits_{0}^{1}{{{x}^{2}}\ln \left( x+1 \right)dx}$. Đặt $\left\{ \begin{array} {} u=\ln \left( x+1 \right) \\ {} dv={{x}^{2}}dx \\ \end{array} \right.\Rightarrow \left\{ \begin{array} {} du=\frac{dx}{x+1} \\ {} dv=\frac{{{x}^{3}}+1}{3} \\ \end{array} \right.$
Ta có: $\int\limits_{0}^{1}{{{x}^{2}}\ln \left( x+1 \right)dx}=\left. \frac{{{x}^{3}}+1}{3}\left. \ln \left( x+1 \right) \right| \right|_{0}^{1}-\int\limits_{0}^{1}{\left( {{x}^{2}}-x+1 \right)dx}=\frac{1}{18}\left( 12\ln 2-5 \right)$
Do đó $V=\frac{\pi }{18}\left( 12\ln 2-5 \right)$. Chọn D.
| Ví dụ 7: Tính thể tích hình khối do hình phẳng giới hạn bởi các đường $x={{y}^{2}}+5;\,\,x=3-y$ quay quanh $Oy.$
A. $V=\frac{153}{3}\pi .$ B. $V=\frac{9}{2}\pi .$ C. $V=\frac{81}{10}\pi .$ D. $V=\frac{153}{5}\pi .$ |
Lời giải:
Tung độ giao điểm là: $-{{y}^{2}}+5=3-y\Leftrightarrow \left[ \begin{array} {} y=-1 \\ {} y=2 \\ \end{array} \right.$
$\Rightarrow V=\pi \int\limits_{-1}^{2}{\left| {{\left( -{{y}^{2}}+5 \right)}^{2}}-{{\left( 3-y \right)}^{2}} \right|dy}\xrightarrow{CASIO}V=\frac{153}{5}\pi $
Vậy $V=\frac{153}{5}\pi $ (đvtt). Chọn D.
| Ví dụ 8: Gọi $\left( H \right)$ là hình phẳng giới hạn bởi $\left( C \right):y={{2}^{x}},\,\,\left( d \right):y=-x+a$ và trục $Oy.$ Biết rằng $\left( C \right)$ và $\left( d \right)$ cắt nhau tại một điểm duy nhất có hoành độ bằng 1. Tính thể tích $V$ của khối tròn xoay sinh bởi $\left( H \right)$ khi nó quay quanh trục $Ox.$
A. $V=\left( \frac{19}{3}-\frac{3}{\ln 4} \right)\pi .$ B. $V=\left( \frac{19}{3}+\frac{3}{\ln 4} \right)\pi .$ C. $V=\left( \frac{35}{3}-\frac{3}{\ln 4} \right)\pi .$ D. $V=\left( \frac{35}{3}+\frac{3}{\ln 4} \right)\pi .$ |
Lời giải:
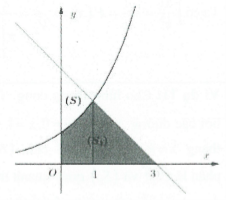
Theo đề bài ta có $2=-1+a\Rightarrow a=3\Rightarrow (d):y=-x+3$.
Gọi ${{V}_{1}}$ là thể tích khối tròn xoay thu được khi quay hình phẳng $\left( {{S}_{1}} \right)$ được giới hạn bởi các đường $\left( C \right),\,\,\,\left( d \right),\,\,Oy,\,\,Ox$ như hình bên quanh trục $Ox$ $\Rightarrow {{V}_{1}}=\pi \int\limits_{0}^{1}{{{\left( {{2}^{x}} \right)}^{2}}dx}+\pi \int\limits_{1}^{3}{{{\left( 3-x \right)}^{2}}dx}$
$\Rightarrow {{V}_{1}}=\pi \left( \frac{8}{3}-\frac{3}{\ln 4} \right).$
Gọi ${{V}_{2}}$ là thể tích khối tròn xoay thu được khi quay hình phẳng được giới hạn bởi các đường $\left( d \right),\,\,Ox$ như hình bên quanh trục hoành,
Suy ra ${{V}_{2}}=\pi \int\limits_{0}^{3}{{{\left( 3-x \right)}^{2}}dx}=9\pi .$ Khi đó $V={{V}_{2}}-{{V}_{1}}=\left( \frac{19}{3}-\frac{3}{\ln 4} \right)\pi .$ Chọn A.
| Ví dụ 9: Để tạo ra những chiếc chậu hoa hình quả lê, người ta dùng một chiếc khuôn là đường cong có phương trình trong hệ trục tọa độ là $y=\sqrt{{{x}^{3}}\left( k-x \right)}\,\,\left( k>0 \right).$ Biết rằng mỗi đơn vị trong hệ trục tọa độ $Oxy$ tương ứng với chiều dài 1 dm. Hãy xác định $k$ để thể tích chậu hoa là $12,15\pi $ dm3.
A. k = 2. B. k = 4. C. k = 3. D. $k=\sqrt[4]{243}$. |
Lời giải:
Ta có: ${{y}^{2}}={{x}^{3}}\left( k-x \right)\Rightarrow $ đồ thị cắt trục $Ox$ tại điểm $\left( 0;k \right).$
Thể tích của chậu hoa là: $V=\pi \int\limits_{0}^{k}{{{x}^{3}}\left( k-x \right)dx}=\left. \pi \left( k\frac{{{x}^{4}}}{4}-\frac{{{x}^{5}}}{5} \right) \right|_{0}^{k}=\pi \left( \frac{{{k}^{5}}}{4}-\frac{{{k}^{5}}}{5} \right)=12,15\pi $
$\Leftrightarrow {{k}^{5}}=243\Leftrightarrow k=3$. Chọn C.
| Ví dụ 10: Cho hình thang cong $\left( H \right)$ giới hạn bởi các đường $y=\frac{1}{x};\,\,y=0;\,\,x=1;\,\,x=5$. Đường thẳng $x=k$ với $1<k<5$ chia $\left( H \right)$ thành hai phần là $\left( {{S}_{1}} \right)$ và $\left( {{S}_{2}} \right)$ quay quanh trục $Ox$ ta thu được hai khối tròn xoay có thể tích lần lượt là ${{V}_{1}}$ và ${{V}_{2}}.$ Xác đinh $k$ để ${{V}_{1}}=2{{V}_{2}}.$ 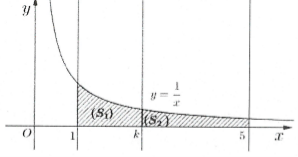
A. $k=\frac{5}{3}.$ B. $k=\frac{15}{7}.$ C. $k=\ln 5.$ D. $k=\sqrt[3]{25}.$ |
Lời giải:
Ta có $\int{\frac{dx}{{{x}^{2}}}}=-\frac{1}{x}=F\left( x \right)\Rightarrow \frac{{{V}_{1}}}{{{V}_{2}}}=\frac{\pi \int\limits_{1}^{k}{{{\left( \frac{1}{x} \right)}^{2}}dx}}{\pi \int\limits_{k}^{5}{{{\left( \frac{1}{x} \right)}^{2}}dx}}=\frac{F\left( k \right)-F\left( 1 \right)}{F\left( 5 \right)-F\left( k \right)}=2\Leftrightarrow k=\frac{15}{7}.$ Chọn B.
| Ví dụ 11: Cho hình thang cong $\left( H \right)$ giới hạn bởi các đường $y=\sqrt{x};\,\,y=0;\,\,x=1;\,\,x=7$. Đường thẳng $x=k$ với $1<k<7$ chia $\left( H \right)$ thành hai phần là $\left( {{S}_{1}} \right)$ và $\left( {{S}_{2}} \right)$ quay quanh trục $Ox$ ta thu được hai khối tròn xoay có thể tích lần lượt là ${{V}_{1}}$ và ${{V}_{2}}.$ Xác đinh $k$ để ${{V}_{1}}=2{{V}_{2}}.$ 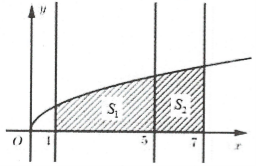 A. $k=33.$ B. $k=\sqrt{33}.$ C. $k=\frac{33}{2}.$ D. $k=\sqrt[3]{33}.$ |
Lời giải:
Ta có $\int{x}=\frac{{{x}^{2}}}{2}=F\left( x \right)\Rightarrow \frac{{{V}_{1}}}{{{V}_{2}}}=\frac{\pi \int\limits_{1}^{k}{{{\left( \sqrt{x} \right)}^{2}}dx}}{\pi \int\limits_{k}^{7}{{{\left( \sqrt{x} \right)}^{2}}dx}}=\frac{F\left( k \right)-F\left( 1 \right)}{F\left( 7 \right)-F\left( k \right)}=2\Leftrightarrow F\left( k \right)-\frac{1}{2}=2\left( \frac{49}{2}-F\left( k \right) \right)$
$\Rightarrow F\left( k \right)=\frac{33}{2}\Rightarrow k=\sqrt{33}.$ Chọn B.
| Ví dụ 12: [Đề Tham khảo Bộ Giáo dục và Đào tạo 2017] Tính thể $V$ của phần vật thể giới hạn bởi hai mặt phẳng $x=1$ và $x=3,$ biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục $Ox$ tại điểm có hoành độ $x\,\,\left( 1\le x\le 3 \right)$ thì được một thiết diện là một hình chữ nhật có độ dài hai cạnh là $3x$ và $\sqrt{3{{x}^{2}}-2}$?
A. $V=32+2\sqrt{15}.$ B. $V=\frac{124\pi }{3}.$ C. $V=\frac{124}{3}.$ D. $V=\left( 32+2\sqrt{15} \right)\pi .$ |
Lời giải:
Ta có: $S\left( x \right)={{S}_{HCN}}=3x\sqrt{3{{x}^{2}}-2}\Rightarrow V=\int\limits_{1}^{3}{S\left( x \right)dx}=\int\limits_{1}^{3}{3x\sqrt{3{{x}^{2}}-2}\,dx}=\frac{1}{2}\int\limits_{1}^{3}{\sqrt{3{{x}^{2}}-2}\,d\left( 3{{x}^{2}}-2 \right)}$
$=\frac{1}{3}\left. \sqrt{{{\left( 3{{x}^{2}}-2 \right)}^{3}}} \right|_{1}^{3}=\frac{124}{3}.$ Chọn C.
| Ví dụ 13: Tính thể tích của vật thể nằm giữa hai mặt phẳng $x=0$ và $x=1,$ biết thiết diện của vật thể cắt bởi mặt phẳng $\left( P \right)$ vuông góc với trục $Ox$ tại điểm có hoành độ $x\,\,\left( 0\le x\le 1 \right)$ là một hình chữ nhật có độ dài hai cạnh là $x$ và $\ln \left( {{x}^{2}}+1 \right)$.
A. $\ln 2-1.$ B. $\frac{1}{2}\left( \ln 2-1 \right).$ C. $\ln 2-\frac{1}{2}.$ D. $\frac{1}{2}\ln 2-1.$ |
Lời giải:
Do thiết diện là hình chữ nhật nên diện tích thiết diện là: $S\left( x \right)=x\ln \left( {{x}^{2}}+1 \right)$
Ta có thể tích cần tính là $V=\int\limits_{0}^{1}{x\ln \left( {{x}^{2}}+1 \right)dx}$
$V=\frac{1}{2}\int\limits_{0}^{1}{\ln \left( {{x}^{2}}+1 \right)d\left( {{x}^{2}}+1 \right)=\frac{1}{2}}\left( {{x}^{2}}+1 \right)\left. \ln \left( {{x}^{2}}+1 \right) \right|_{0}^{1}-\frac{1}{2}\int\limits_{0}^{1}{\left( {{x}^{2}}+1 \right)d\left( \ln \left( {{x}^{2}}+1 \right) \right)}$
$\ln 2-\frac{1}{2}\int\limits_{0}^{1}{2xdx=\ln 2-\frac{1}{2}}.$ Chọn C.
| Ví dụ 14: Tính thể tích của vật thể nằm giữa hai mặt phẳng $x=0$ và $x=\pi ,$ biết thiết điện của vật thể cắt bởi mặt phẳng $\left( P \right)$ vuông góc với trục $Ox$ tại điểm có hoành độ $x\,\,\left( 0\le x\le \pi \right)$ là một tam giác đều có cạnh bằng $2\sqrt{\sin x}$.
A. $V=8\sqrt{3}.$ B. $V=2\pi \sqrt{3}.$ C. $V=2\sqrt{3}.$ D. $V=\sqrt{3}.$ |
Lời giải:
Diện tích thiết diện là $S\left( x \right)=\frac{{{\left( 2\sqrt{\sin x} \right)}^{2}}.\sqrt{3}}{4}=\sqrt{3}\sin x$
Ta có thể tích cần tính là $V=\int\limits_{0}^{\pi }{\sqrt{3}\sin xdx=-\left. \sqrt{3}\,\cos x \right|}_{0}^{\pi }=2\sqrt{3}.$ Chọn C.
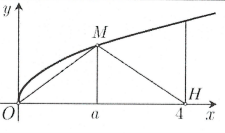
| Ví dụ 15: [Đề Chuyên Đại học Vinh 2017] Gọi $V$ là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường $y=\sqrt{x};\,\,y=0;\,\,x=4$ quanh trục $Ox.$ Đường thẳng $x=a\,\,\left( 0<a<4 \right)$ cắt đồ thị hàm số $y=\sqrt{x}$ tại $M$ (hình vẽ bên). Gọi ${{V}_{1}}$ là thể tích khối tròn xoay tạo thành khi quay tam giác $OMH$ quanh trục $Ox.$ Biết rằng $V=2{{V}_{1}}$. Khi đó
A. $a=2\sqrt{2}.$ B. $a=\frac{5}{2}.$ C. $a=2.$ D. $a=3.$ |
Lời giải:
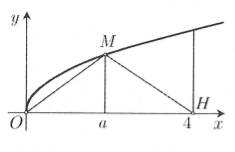
Ta có $V=\pi \int\limits_{0}^{4}{xdx=8\pi \Rightarrow }\,\,{{V}_{1}}=4\pi .$
Gọi $N$ là giao điểm của đường thẳng $x=a$ và trục hoành. Khi đó ${{V}_{1}}$ là thể tích tạo được khi xoay hai tam giác $OMN$ và $MNH$ quanh trục $Ox$ với $N$ là hình chiếu của $M$ trên $OH.$
Ta có ${{V}_{1}}=\frac{1}{3}\pi a{{\left( \sqrt{a} \right)}^{2}}+\frac{1}{3}\pi \left( 4-a \right){{\left( \sqrt{a} \right)}^{2}}=\frac{4}{3}\pi a=4\pi \Leftrightarrow a=3.$
Chọn D.
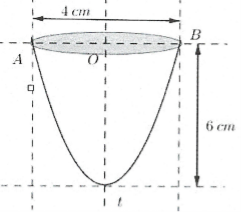
| Ví dụ 16: Có một vật thể là hình tròn xoay có dạng giống như một cái ly như hình vẽ dưới đây: Người ta đo được đường kính của miệng ly là $4\,\,cm$ và chiều cao là $6\,\,cm.$ Biết rằng thiết diện của chiếc ly cắt bởi mặt phẳng qua trục đối xứng là một parabol. Tính thể tích $V\,\,\left( c{{m}^{3}} \right)$ của vật thể đã cho?
A. $V=\frac{72\pi }{5}.$ B. $V=12.$ C. $V=12\pi .$ D. $V=\frac{72}{5}.$ |
Lời giải:
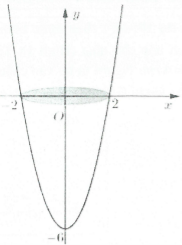
Chọn hệ trục tọa độ như hình suy ra phương trình Parabol là: $y=\frac{3{{x}^{2}}-12}{2}\Rightarrow {{x}^{2}}=\frac{2y+12}{3}.$
Thể tích của vật là thể tích khối tròn xoay khi quay hình $\left( H \right)$ giới hạn bởi các đường $x=\sqrt{\frac{2y+12}{3}},\,\,x=0,\,\,y=-6;\,\,y=0$ quanh trục tung.
Khi đó $V=\pi \int\limits_{-6}^{0}{\frac{2y+12}{3}dy=\left. \pi \left( \frac{1}{3}{{y}^{2}}+4y \right) \right|}_{-6}^{0}=12\pi .$ Chọn C.
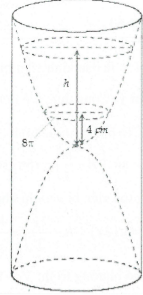
| Ví dụ 17: Một chiếc đồng hồ cát như hình vẽ, gồm hai phần đối xứng nhau qua mặt nằm ngang và đặt trong một hình trụ. Thiết diện thẳng đứng qua trục của nó là hai parabol chung đỉnh và đối xứng nhau qua mặt nằm ngang. Ban đầu lượng cát dồn hết ở phần trên của đồng hồ thì chiều cao h của mực cát bằng $\frac{3}{4}$chiều cao của bên đó (xem hình). Cát chảy từ trên xuống dưới với lưu lượng không đổi 2,90 cm3/ phút. Khi chiều cao của cát còn 4 cm thì bề mặt trên cùng của cát tạo thành một đường tròn chu vi 8$\pi $ cm (xem hình). Biết sau 30 phút thì cát chảy hết xuống phần bên dưới của đồng hồ. Hỏi chiều cao của khối trụ bên ngoài là bao nhiêu cm? (Kết quả làm tròn đến hàng đơn vị)
A. 8 cm. B. 12 cm. C. 9 cm. D. 10 cm. |
Lời giải:
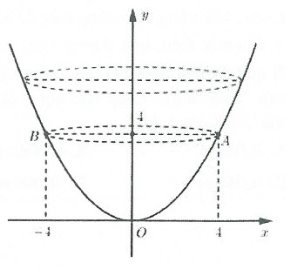
Gọi (α) là mặt phẳng song song với đáy của hình trụ và cắt đồng hồ cát.
Khi đó mặt cắt là một hình tròn có bán kính là $x$ nên diện tích hình tròn là ${{S}_{t}}=\pi {{R}^{2}}=\pi {{x}^{2}}$.
Chọn hệ trục tọa độ $Oxy$ như hình vẽ, gọi phương trình của parabol $\left( P \right)$ là $y=a{{x}^{2}}+bx+c$.
Vì $\left( P \right)$ đi qua điểm $O\left( 0;0 \right),\,\,A\left( 4;4 \right),\,\,B\left( 4;-4 \right)$
Nên phương trình $\left( P \right):$ $y=\frac{{{x}^{2}}}{4}\Rightarrow {{x}^{2}}=4y\Rightarrow S=4\pi y.$
→ Thể tích cát ban đầu là $V=\int\limits_{0}^{h}{{{S}_{t}}dy}$ vì mặt cắt vuông góc với $Oy.$ Suy ra $V=\int\limits_{0}^{h}{\left( 4\pi y \right)dy}$ mà thể tích khối cát ${{V}_{c}}=2,9.30=87\,\,c{{m}^{3}}.$
$\Rightarrow \int\limits_{0}^{h}{\left( 4\pi y \right)dy=}\,87\Leftrightarrow \left. 2\pi {{y}^{2}} \right|_{0}^{h}=87\Rightarrow 2\pi {{h}^{2}}=87\Rightarrow h=\sqrt{\frac{87}{2\pi }}.$
Vậy chiều cao của khối trụ bên ngoài là $2.\frac{4}{3}.h=2.\frac{4}{3}.\sqrt{\frac{87}{2\pi }}\approx 9,92\,\,cm$. Chọn D.
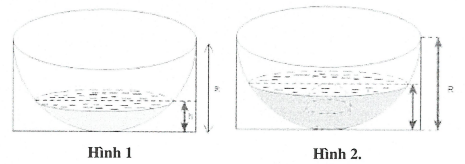
| Ví dụ 18: Một chậu nước hình bán cầu băng nhôm có bán kính $R=10\,\,cm,$ đặt trong một khung hình hộp chữ nhật (Hình 1). Trong chậu có chứa sẵn một khối nước hình chỏm cầu có chiều cao $h=4\,\,cm.$ Người ta bỏ vào chậu một viên bi hình cầu bằng kim loại thì mặt nước dâng lên vừa phủ kín viên bi (Hình 2). Bán kính của viên bi gần bằng:
A. 9,63. B. 2,09. C. 1,72. D. 4,01. |
Lời giải:
Gọi $x$ là bán kính viên bi hình cầu. Điều kiện: $0<2x<10\Leftrightarrow 0<x<5$
Chú ý: Công thức thể tích chỏm cầu: $V=\pi {{h}^{2}}\left( R-\frac{h}{3} \right).$
Thể tích khối nước hình chỏm cầu khi chưa thả viên bi vào:
${{V}_{1}}=\pi {{h}^{2}}\left( R-\frac{h}{3} \right)=16\pi \left( 10-\frac{4}{3} \right)=\frac{416}{3}\pi $
Khi thả viên bi vào thì khối chỏm cầu gồm khối nước và viên bi có thể tích là:
${{V}_{2}}=\pi {{\left( 2x \right)}^{2}}\left( R-\frac{2x}{3} \right)=\frac{4\pi {{x}^{2}}\left( 30-2x \right)}{3}$
Ta có phương trình: ${{V}_{2}}-{{V}_{1}}=\frac{4}{3}\pi {{x}^{3}}\Leftrightarrow 4\pi {{x}^{2}}\left( 30-2x \right)-416\pi =4\pi {{x}^{3}}$
$\Leftrightarrow 3{{x}^{3}}-30{{x}^{2}}+104=0\Leftrightarrow \left[ \begin{align} & x\approx 9,626>5\,\,\,(lo{}^\text{1}i) \\ & x\approx 2,0940<5 \\ & x=-1,72\,\,(lo{}^\text{1}i) \\ \end{align} \right..$ Chọn B.