Bài tập Góc giữa cạnh bên và mặt đáy – có đáp án chi tiết
Phương pháp tính góc giữa cạnh bên và mặt đáy
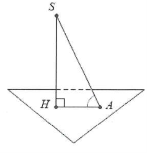
Tìm góc giữa cạnh bên SA và mặt đáy (ABC)
Gọi H là hình chiếu vuông góc của S trên mặt phẳng đáy (ABC).
Như vậy HA là hình chiếu vuông góc của SA trên (ABC).
Vậy $\left( \widehat{SA;\left( ABC \right)} \right)=\widehat{\left( SA;HA \right)}=\widehat{SAH}.$
Bài tập tính góc giữa cạnh bên và mặt đáy có Lời giải chi tiết
| Bài tập 1: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, có $AB=a;BC=a\sqrt{3}$. Biết $SA\bot \left( ABC \right)$, SB tạo với đáy một góc $60{}^\circ $ và M là trung điểm của BC.
a) Tính cosin góc giữa SC và mặt phẳng (ABC). b) Tính cosin góc giữa SM và mặt phẳng (ABC). |
Lời giải chi tiết
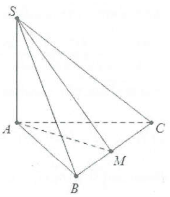
a) Do $SA\bot \left( ABC \right)\Rightarrow \left( \widehat{SB;\left( ABC \right)} \right)=\widehat{SBA}=60{}^\circ .$
Do đó $SA=AB\tan \widehat{SBA}=a\tan 60{}^\circ =a\sqrt{3}.$
Ta có: $AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=2a;\widehat{\left( SC;\left( ABC \right) \right)}=\widehat{SCA}.$
Khi đó: $\cos \widehat{SCA}=\frac{AC}{SC}=\frac{AC}{\sqrt{S{{A}^{2}}+A{{C}^{2}}}}=\frac{2a}{\sqrt{3{{a}^{2}}+4{{a}^{2}}}}=\frac{2}{\sqrt{7}}.$
b) Do $SA\bot \left( ABC \right)\Rightarrow \widehat{\left( SM;\left( ABC \right) \right)}=\widehat{SMA}=\varphi .$
Ta có: $AM=\sqrt{A{{B}^{2}}+B{{M}^{2}}}=\sqrt{{{a}^{2}}+{{\left( \frac{a\sqrt{3}}{2} \right)}^{2}}}=\frac{a\sqrt{7}}{2}.$
Khi đó $\cos \varphi =\frac{AM}{SM}=\frac{AM}{\sqrt{S{{A}^{2}}+A{{M}^{2}}}}=\frac{\sqrt{133}}{19}.$
| Bài tập 2: Cho hình chóp S.ABCD, đáy là hình chữ nhật có $AB=2a;AD=a$. Tam giác (SAB) đều và thuộc mặt phẳng vuông góc với đáy.
a) Tính góc giữa SB, SC và mặt phẳng (ABCD). b) Gọi I là trung điểm của BC. Tính tan góc giữa SI và mặt phẳng (ABCD). |
Lời giải chi tiết
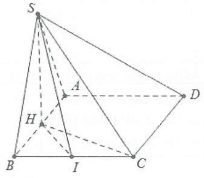
a) Gọi H là trung điểm của AB ta có: $SH\bot AB$
Mặt khác $\left\{ \begin{array} {} \left( SAB \right)\bot \left( ABCD \right) \\ {} AB=\left( SAB \right)\cap \left( ABCD \right) \\ \end{array} \right.\Rightarrow SH\bot \left( ABCD \right).$
Tam giác SAB đều cạnh 2a nên $SH=a\sqrt{3},$
$HC=\sqrt{H{{B}^{2}}+B{{C}^{2}}}=a\sqrt{2}.$
Do $SH\bot \left( ABCD \right)\Rightarrow \left( \widehat{SB;\left( ABCD \right)} \right)=\widehat{SBH}=60{}^\circ $
$\left( \widehat{SC;\left( ABCD \right)} \right)=\widehat{SCH}$ và $\tan \widehat{SCH}=\frac{SH}{HC}=\sqrt{\frac{3}{2}}.$
b) Ta có: $HI=\sqrt{H{{B}^{2}}+B{{I}^{2}}}=\sqrt{{{a}^{2}}+{{\left( \frac{a}{2} \right)}^{2}}}=\frac{a\sqrt{5}}{2}.$
Mặt khác $\left( \widehat{SI;\left( ABCD \right)} \right)=\widehat{SIH}$ và $\widehat{SIH}=\frac{SH}{SI}=a\sqrt{3}:\frac{a\sqrt{5}}{2}=\frac{2\sqrt{15}}{5}.$
| Bài tập 3: Cho hình chóp S.ABCD, có đáy là nửa lục giác đều cạnh a, $AD=2a$. Biết $SA\bot \left( ABCD \right)$ và đường thẳng SB tạo với đáy một góc $45{}^\circ .$
a) Tính cosin góc tạo bởi các cạnh SC, SD và mặt đáy (ABCD). b) Gọi I là trung điểm của CD, tính tan góc tạo bởi SI và mặt phẳng (ABCD). |
Lời giải chi tiết
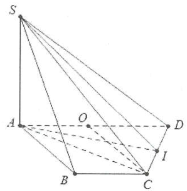
a) Gọi O là trung điểm của AD $\Rightarrow $ OABC là hình thoi cạnh a $\Rightarrow CO=a=\frac{1}{2}AD\Rightarrow \Delta ACD$ vuông tại C.
Do $SA\bot \left( ABCD \right)\Rightarrow \widehat{\left( SB;\left( ABCD \right) \right)}=\widehat{SBA}=45{}^\circ .$
Do đó $SA=AB\tan 45{}^\circ =a.$
$AC=\sqrt{A{{D}^{2}}-C{{D}^{2}}}=a\sqrt{3}\Rightarrow \cos \widehat{\left( SC;\left( ABC \right) \right)}=\cos \widehat{SCA}$
$=\frac{AC}{SC}=\frac{AC}{\sqrt{S{{A}^{2}}+A{{C}^{2}}}}=\frac{a\sqrt{3}}{\sqrt{{{a}^{2}}+3{{a}^{2}}}}=\frac{\sqrt{3}}{2}.$
$\cos \left( \widehat{SD;\left( ABCD \right)} \right)=\cos \widehat{SDA}=\frac{AD}{\sqrt{S{{A}^{2}}+A{{D}^{2}}}}=\frac{2}{\sqrt{5}}.$
b) Ta có: $AI=\sqrt{A{{C}^{2}}+C{{I}^{2}}}=\sqrt{3{{a}^{2}}+{{\left( \frac{a}{2} \right)}^{2}}}=\frac{a\sqrt{13}}{2}.$
Do đó $\tan \widehat{\left( SI;\left( ABCD \right) \right)}=\tan \widehat{SIA}=\frac{SA}{AI}=\frac{2}{\sqrt{13}}.$