Tính Khoảng cách từ một điểm trên mặt phẳng đáy tới mặt phẳng chứa đường cao
Xét bài toán khoảng cách trong không gian.
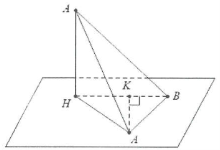
Cho hình chóp có đỉnh S có hình chiếu vuông góc lên mặt đáy là H. Tính khoảng cách từ điểm A bất kì đến mặt bên $\left( SHB \right)$.
Kẻ $AH\bot HB$ ta có:
$\left\{ \begin{array} {} AK\bot HB \\ {} AK\bot SH \\ \end{array} \right.\Rightarrow AK\bot \left( SHB \right)$
Suy ra $d\left( A;\left( SHB \right) \right)=AK$.
Cách tính:
Ta có: $d\left( A;\left( SHB \right) \right)=AK=\frac{2{{S}_{AHB}}}{HB}$
$=AB\sin \widehat{ABK}=AH.\sin \widehat{AHK}$.
Bài tập tính khoảng cách từ một điểm có đáp án chi tiết
| Bài tập 1: Cho hình chóp S.ABC có đáy là tam giác ABC có $AB=3a,BC=2a,\widehat{ABC}=60{}^\circ $. Biết $SA\bot \left( ABC \right)$.
a) Tính khoảng cách từ C đến mặt phẳng $\left( SAB \right)$. b) Tính khoảng cách từ B đến mặt phẳng $\left( SAC \right)$. |
Lời giải chi tiết
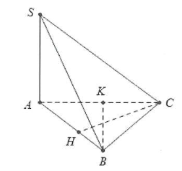
a) Dựng $CH\bot AB$ ta có: $\left\{ \begin{array} {} CH\bot AB \\ {} CH\bot SA \\ \end{array} \right.\Rightarrow CH\bot \left( SAB \right)$
Do đó
$d\left( C;\left( SAB \right) \right)=CH=CB\sin \widehat{ABH}=2a\sin 60{}^\circ =a\sqrt{3}$.
b) Dựng $CK\bot AC\Rightarrow CK\bot \left( SAC \right)$.
Ta có: $d\left( B;\left( SAC \right) \right)=CH=\frac{2{{S}_{ABC}}}{AC}=\frac{AB.BC\sin \widehat{ABC}}{AC}$
Trong đó $A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}-2BA.BC\cos \widehat{B}$
$\Rightarrow AC=a\sqrt{7}\Rightarrow d\left( B;\left( SAC \right) \right)=\frac{3a.2a.\sin 60{}^\circ }{a\sqrt{7}}=\frac{3a\sqrt{21}}{7}$.
| Bài tập 2: Cho hình chóp S.ABCD có đáy là hình chữ nhật với $B=a,AD=a\sqrt{3}$. Tam giác SAB cân tại S và thuộc mặt phẳng vuông góc với đáy. Gọi H là trung tâm của AB.
a) Tính khoảng cách từ A đến mặt phẳng $\left( SHD \right)$. b) Tính khoảng cách từ D đến mặt phẳng $\left( SHC \right)$. |
Lời giải chi tiết
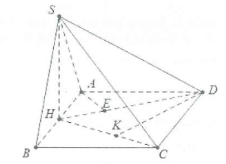
a) Do tam giác SAB cân tại S nên $SH\bot AB$.
Ta có: $HA=HD=\frac{a}{2}$.
Mặt khác $\left( SAB \right)\bot \left( ABCD \right)\Rightarrow SH\bot \left( ABCD \right)$.
Dựng $AE\bot DH\Rightarrow AE\bot \left( SHD \right)\Rightarrow d\left( A;\left( SHD \right) \right)=AE$.
Mặt khác $AE=\frac{AH.AD}{\sqrt{A{{H}^{2}}+A{{D}^{2}}}}=\frac{a\sqrt{39}}{13}$.
b) Dựng $DK\bot CH\Rightarrow d\left( D;\left( SHC \right) \right)=DK$.
Ta có: $CH=\sqrt{H{{B}^{2}}+B{{C}^{2}}}=\frac{a\sqrt{13}}{2}$, ${{S}_{HCD}}=\frac{1}{2}CD.d\left( H;CD \right)=\frac{1}{2}\text{.}a\text{.}a\sqrt{3}=\frac{{{a}^{2}}\sqrt{3}}{2}$.
Do đó $d\left( D;\left( SHC \right) \right)=\frac{2{{S}_{HCD}}}{CH}=\frac{2a\sqrt{39}}{13}$.
| Bài tập 3: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B có $AD=3a$, $AB=BC=2a$. Biết $SA\bot \left( ABCD \right)$.
a) Tính khoảng cách từ C đến mặt phẳng $\left( SAD \right)$. b) Tính khoảng cách từ D đến mặt phẳng $\left( SAC \right)$. |
Lời giải chi tiết
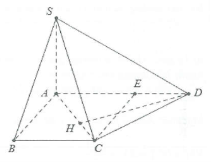
a) Dựng $CE\bot AD\Rightarrow CE\bot \left( SAD \right)$.
Khi đó $d\left( C;\left( SAD \right) \right)=CE$, do ABCE là hình vuông cạnh $2a$ nên $CE=AE=2a\Rightarrow d\left( C;\left( SAD \right) \right)=2a$.
b) Dựng $DH\bot AC\Rightarrow DH\bot \left( SAC \right)$.
Khi đó $d\left( D;\left( SAC \right) \right)=DH$.
Ta có: ABCE là hình vuông nên $\widehat{CAD}=45{}^\circ $.
Do đó $DH=ADsin45{}^\circ =3a.\frac{\sqrt{2}}{2}=\frac{3a\sqrt{2}}{2}$.
| Bài tập 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh $5a$. Hình chiếu vuông góc của đỉnh S trên mặt phẳng $\left( ABCD \right)$ trùng với trọng tâm H của tam giác ABD.
a) Tính khoảng cách từ B đến mặt phẳng $\left( SAC \right)$. b) Tính khoảng cách từ C đến mặt phẳng $\left( SHD \right)$. |
Lời giải chi tiết
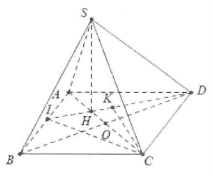
a) Do H là trọng tâm tam giác ABD $\Rightarrow H\in AC$.
Gọi O là tâm của hình vuông ABCD $\Rightarrow BO\bot AC$.
Mặt khác $BO\bot SH\Rightarrow BO\bot \left( SAC \right)$
Khi đó $d\left( B;\left( SAC \right) \right)=BO=\frac{5a\sqrt{2}}{2}$.
b) Dựng $CK\bot HD\Rightarrow CK\bot \left( SHD \right)\Rightarrow d\left( C;\left( SHD \right) \right)=CK$.
Gọi I là trung điểm của AB thì $H=DI\cap AO$.
Khi đó: $CK=\frac{2{{S}_{ICD}}}{DI}=\frac{2.\frac{1}{2}{{S}_{ABCD}}}{DI}=\frac{25{{a}^{2}}}{\sqrt{D{{A}^{2}}+A{{I}^{2}}}}=\frac{25{{a}^{2}}}{\sqrt{25{{a}^{2}}+{{\left( \frac{5a}{2} \right)}^{2}}}}=2a\sqrt{5}$.
| Bài tập 5: Cho hình chóp S.ABCD có đáy ABCD nửa lục giác đều cạnh $a$, với $AB=2a$. Biết $SA\bot \left( ABCD \right)$ và mặt phẳng $\left( SBC \right)$ tạo với đáy một góc $60{}^\circ $.
a) Tính khoảng cách từ C đến mặt phẳng $\left( SAB \right)$. b) Tính khoảng cách từ D đến mặt phẳng $\left( SAC \right)$. |
Lời giải chi tiết
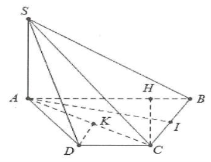
a) Tứ giác ABCD là nửa lục giác đều cạnh $a$ nên nó nội tiếp đường tròn đường kính $AB=2a$.
Dựng $CH\bot AB\Rightarrow CH\bot \left( SAB \right)\Rightarrow d\left( C;\left( SAB \right) \right)=CH$.
Mặt khác $\widehat{ABC}=60{}^\circ \Rightarrow CH=BC\sin 60{}^\circ =\frac{a\sqrt{3}}{2}$.
Vậy $d\left( C;\left( SAB \right) \right)=\frac{a\sqrt{3}}{2}$.
b) Dựng $DK\bot AC\Rightarrow DK\bot \left( SAC \right)\Rightarrow d\left( D;\left( SAC \right) \right)=DK$.
Do $\widehat{DCB}=120{}^\circ ,\widehat{ACB}=90{}^\circ \Rightarrow \widehat{ACD}=30{}^\circ \Rightarrow DK=CD\sin \widehat{DCK}=a\sin 30{}^\circ =\frac{a}{2}$.
| Bài tập 6: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có diện tích bằng 2, $AB=\sqrt{2},BC=2$. Gọi M là trung điểm của CD, hai mặt phẳng $\left( SBD \right)$ và $\left( SAM \right)$ cùng vuông góc với đáy. Tính khoảng cách từ B đến mặt phẳng $\left( SAM \right)$. |
Lời giải chi tiết
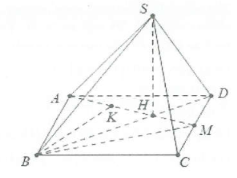
Ta có ${{S}_{ABCD}}=2{{S}_{\Delta ABC}}=2{{S}_{\Delta MAB}}=2\Rightarrow {{S}_{\Delta ABC}}={{S}_{\Delta MAB}}=1$.
$\Rightarrow {{S}_{\Delta ABC}}=\frac{1}{2}.AB.BC.\sin \widehat{ABC}=1\Rightarrow \sin \widehat{ABC}=\frac{1}{\sqrt{2}}$.
Do đó $\widehat{ABC}=45{}^\circ \Rightarrow \widehat{ADM}=45{}^\circ $.
Áp dụng định lý Cosin trong tam giác ADM, ta có:
$AM=\sqrt{A{{D}^{2}}+D{{M}^{2}}-2.AD.DM.cos\widehat{ADM}}=\frac{\sqrt{10}}{2}$
Gọi H là giao điểm của AM và BD $\Rightarrow SH\bot \left( ABCD \right)$.
Kẻ BK vuông góc với AM, $K\in AM\Rightarrow BK\bot AM$ $\left( 1 \right)$.
Ta có $\left( SAM \right)\cap \left( SBD \right)=SH\Rightarrow SH\bot \left( ABCD \right)\Rightarrow SH\bot BK$ $\left( 2 \right)$.
Từ $\left( 1 \right)$,$\left( 2 \right)$$\Rightarrow BK\bot \left( SAM \right)\Rightarrow d\left( B;\left( SAM \right) \right)=BK$.
Mặt khác ${{S}_{\Delta MAB}}=\frac{1}{2}.BK.AM\Rightarrow BK=\frac{2.{{S}_{\Delta MAB}}}{AM}=\frac{4}{\sqrt{10}}=\frac{2\sqrt{10}}{5}$.
| Bài tập 7: Cho hình lăng trụ $ABCD.A’B’C’D’$ có đáy là hình chữ nhật ABCD có hai đường chéo $AC=BD=2a$. Tam giác A’BD vuông cân tại A’ và nằm trong mặt phẳng vuông góc với đáy. Mặt phẳng $\left( A’AB \right)$ tạo với đáy một góc $60{}^\circ $. Tính khoảng cách $d\left( B’;\left( A’BD \right) \right)$. |
Lời giải chi tiết
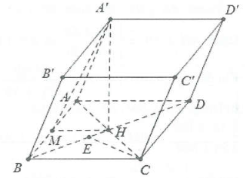
Gọi H là tâm hình chữ nhật ABCD
$\Rightarrow $$HA=HC\Rightarrow A’H\bot BD$ (Do $\Delta A’BD$ cân tại A’).
Do $\left( A’BD \right)\bot \left( ABCD \right)\Rightarrow A’H\bot \left( ABCD \right)$.
Ta có: $A’H=\frac{1}{2}BD=a$ (trong tam giác vuông đường trung tuyến ứng cạnh huyền bằng nửa cạnh ấy).
Dựng $HM\bot AB\Rightarrow AB\bot \left( A’HM \right)\Rightarrow \overset\frown{A’MH}=60{}^\circ $
+) Khi đó: $HM\tan 60{}^\circ =A’H\Rightarrow HM=\frac{a}{\sqrt{3}}$
$\Rightarrow AD=2HM=\frac{2a}{\sqrt{3}}\Rightarrow AB=2a\sqrt{\frac{2}{3}}$
Do: $A’D//B’C\Rightarrow B’C//\left( A’BD \right)\Rightarrow d\left( B’;\left( A’BD \right) \right)=d\left( C;\left( A’BD \right) \right)$.
Ta có: $CE=\frac{CD.CB}{BD}=\frac{2a\sqrt{2}}{3}$. Vậy $d\left( B’;\left( A’BD \right) \right)=\frac{2a\sqrt{2}}{3}$.