BÀI TẬP QUỸ TÍCH CỰC ĐẠI, CỰC TIỂU GIAO THOA ÁNH SÁNG CÓ ĐÁP ÁN CHI TIẾT
| Bài tập 1: Để khảo sát giao thoa sóng cơ, người ta bố trí trên mặt nước nằm ngang hai nguồn kết hợp ${{S}_{1}}$ và ${{S}_{2}}$. Hai nguồn này dao động điều hòa theo phương thẳng đứng, cùng pha. Xem biên độ sóng không thay đổi trong quá trình truyền sóng. Các điểm thuộc mặt nước và nằm trên đường trung trực của đoạn ${{S}_{1}}{{S}_{2}}$ sẽ:
A. dao động với biên độ bằng nửa biên độ cực đại B. dao động với biên độ cực tiểu. C. dao động với biên độ cực đại. D. không dao động. |
Lời giải chi tiết:
Hai nguồn dao động cùng pha do đó khi xảy ra giao thoa sóng cơ, các điểm nằm trên đường trung trực của đoạn ${{S}_{1}}{{S}_{2}}$ sẽ dao động với biên độ cực đại. Chọn C.
| Bài tập 2: Tại hai điểm M và N trong một môi trường truyền sóng có hai nguồn sóng kết hợp cùng phương và cùng pha dao động. Biết biên độ, vận tốc của sóng không đổi trong quá trình truyền, tần số của sóng bằng 40 Hz và có sự giao thoa sóng trong đoạn MN. Trong đoạn MN, hai điểm dao động có biên độ cực đại gần nhau nhất cách nhau 1,5 cm. Vận tốc truyền sóng trong môi trường này bằng:
A. 2,4 m/s B. 1,2 m/s C. 0,3 m/s D. 0,6 m/s |
Lời giải chi tiết:
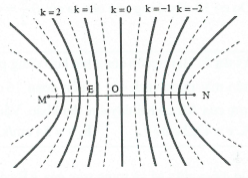
Do 2 nguồn ta xét là hai nguồn cùng pha. Ta có điểm O là trung điểm của MN dao động với biên độ cực đại.
Xét điểm E thuộc dãy cực đại với $k=1$.
Ta có: $EN=ON+OE,ME=OM-OE$
Suy ra $EN-EM=2\text{O}E=\lambda \Rightarrow OE=\frac{\lambda }{2}$
Như vậy $\frac{\lambda }{2}=1,5\Rightarrow \lambda =3cm\Rightarrow v=\lambda .f=1,2m/s$. Chọn B.
| Bài tập 3: Trong một thí nghiệm về giao thoa sóng trên mặt nước, hai nguồn kết hợp A và B dao động với tần số 20 Hz và cùng pha. Tại một điểm M cách nguồn A và B những khoảng ${{d}_{1}}=20cm$ và ${{d}_{2}}=26cm$, sóng có biên độ cực tiểu. Giữa M và đường trung trực của AB có hai dãy cực đại. Tốc độ truyền sóng trên mặt nước là
A. 36 cm/s B. 48 cm/s C. 40 cm/s D. 20 cm/s |
Lời giải chi tiết:
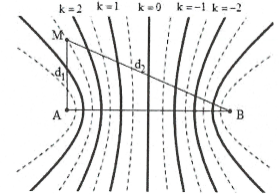
Do giữa M và trung trực của AB có 2 dãy cực đại khác nên M thuộc dãy cực tiểu số 3.
Khi đó ${{d}_{2}}-{{d}_{1}}=2,5\lambda \Rightarrow \lambda =2,4cm$.
Do đó $v=\lambda f=48cm/s$. Chọn B.
| Bài tập 4: Trên mặt một chất lỏng có hai nguồn kết hợp ${{S}_{1}}$ và ${{S}_{2}}$ dao động với cùng pha, cùng tần số $f=50$ Hz. Giữa ${{S}_{1}}$, ${{S}_{1}}$ có 10 hypebol là quỹ tích của các điểm đứng yên. Khoảng cách giữa đỉnh của hai hypebol ngoài cùng là 45cm. Tốc độ truyền sóng trên mặt nước là:
A. v = 4,5 m/s B. v = 5 m/s C. v = 1 m/s D. v = 1 m/s |
Lời giải chi tiết:
Khoảng cách giữa hai đỉnh Hypebol liên tiếp là $\frac{\lambda }{2}$.
Do có 10 dãy đứng yên nên ta có: $9\frac{\lambda }{2}=45\Rightarrow \gamma =10\Rightarrow v=\lambda f=5m/s$. Chọn B.
| Bài tập 5: Hai nguồn sóng kết hợp cùng pha A và B trên mặt nước có tần số f = 24 Hz. Tại điểm M trên mặt nước cách các nguồn đoạn 16 cm và 20,5 cm sóng có biên độ cực đại. Giữa M và trung trực của AB có hai dãy cực đại khác. Vận tốc truyền sóng trên mặt nước là
A. v = 43,2 cm/s B. v = 54 cm/s C. v = 36 cm/s D. v = 20 cm/s |
Lời giải chi tiết:
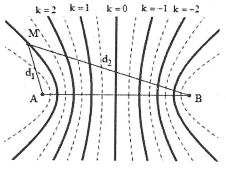
Do điểm giữa M và trung trực của AB có hai dãy cực đại khác nên M thuộc dãy cực đại số 3.
Khi đó ${{d}_{2}}-{{d}_{1}}=3\lambda \Rightarrow \lambda =\frac{20,5-16}{3}=1,5cm$.
Do đó $v=\lambda f=1,5.24=36cm/s$. Chọn C.
| Bài tập 6: Hai nguồn kết hợp A, B cách nhau 45mm ở trên mặt thoáng chất lỏng dao động theo phương trình ${{u}_{1}}={{u}_{2}}=2\cos 100\pi t$ (mm). Trên mặt thoáng chất lỏng có hai điểm M và ${M}’$ ở cùng một phía của đường trung trực của AB thỏa mãn $MA-MB=15mm$ và ${M}’A-{M}’B=35mm$. Hai điểm đó đều nằm trên các vân giao thoa cùng loại và giữa chúng chỉ có một vân loại đó. Vận tốc truyền sóng trên mặt chất lỏng là:
A. 0,5 cm/s B. 0,5 m/s C. 1,5 m/s D. 0,25 m/s |
Lời giải chi tiết:
Giả sử M và ${M}’$ thuộc vân cực đại. Khi đó: $MA-MB=15mm=k\lambda $.
${M}’A-{M}’B=35mm=\left( k+2 \right)\lambda \Rightarrow \frac{k+2}{k}=\frac{35}{15}\Rightarrow k=\frac{3}{2}$ (loại).
Do đó M và ${M}’$ không thuộc vân cực đại.
Nếu M, ${M}’$ thuộc vân cực tiểu thì: $MA-MB=15mm=\left( k+0,5 \right)\lambda $
Và ${M}’A-{M}’B=35mm=\left( k+2,5 \right)\lambda \Rightarrow \frac{k+2,5}{k+0,5}=\frac{35}{15}\Rightarrow k=1\Rightarrow \lambda =\frac{15}{1,5}=10mm$.
$\Rightarrow v=\lambda f=0,5m/s$. Chọn B.
| Bài tập 7: [Trích đề thi Chuyên ĐH Vinh – 2017]. Trên mặt chất lỏng, tại hai điểm ${{S}_{1}}$ và ${{S}_{2}}$, người ta đặt hai nguồn sóng cơ kết hợp dao động điều hòa theo phương thẳng đứng với phương trình ${{u}_{A}}={{u}_{B}}=5\cos 40\pi t$ (${{u}_{A}}$và ${{u}_{B}}$ tính bằng mm, t tính bằng s). Coi biên độ sóng không đổi khi truyền đi. Điểm M trên mặt chất lỏng cách đều hai nguồn S1, S2 dao động với biên độ
A. 5 mm B. 0 mm C. 10 mm D. 5 mm |
Lời giải chi tiết:
Hai nguồn dao động cùng pha cùng biên độ nên điểm thuộc trung trực dao động cực đại với biên độ là $A=2.5=10mm$. Chọn C.
| Bài tập 8: [Trích đề thi Chuyên Lam Sơn – Thanh Hóa 2017]. Trong thí nghiệm về giao thoa sóng mặt nước, hai nguồn kết hợp ${{S}_{1}}$, ${{S}_{2}}$ giống nhau dao động với tần số 13 Hz. Tại điểm M cách A 21 cm cách B 19 cm sóng có biên độ cực đại. Giữa M và đường trung trực của ${{S}_{1}}{{S}_{2}}$ không có cực đại nào khác. Tốc độ truyền sóng trên mặt nước là
A. 28 cm/s B. 46 cm/s C. 40 cm/s D. 26 cm/s |
Lời giải chi tiết:
Giữa M và đường trung trực của ${{S}_{1}}{{S}_{2}}$ không có cực đại nào khác nên M thuộc cực đại thứ nhất ứng với $k=1\Rightarrow MA-MB=2=\lambda \Rightarrow v=26cm/s$. Chọn D.
| Bài tập 9: [Trích đề thi chuyên Lê Hồng Phong – Nam Định]. Tại mặt nước có hai nguồn kết hợp A, B cách 12 cm, dao động cùng pha với tần số 20 Hz. Điểm M cách A, B lần lượt là 4,2 cm và 9 cm. Biết tốc độ sóng truyền trên mặt nước là 32 cm/s. Để điểm M thuộc vân cực tiểu giao thoa thì phải dịch chuyển B theo phương AB ra xa A một khoảng tối thiểu bằng bao nhiêu?
A. 1,62 cm B. 4,8 cm C. 0,83 cm D. 0,45 cm |
Lời giải chi tiết:
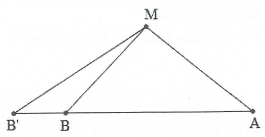
Hai nguồn dao động cùng pha.
Ta có: $\lambda =\frac{v}{f}=1,6cm$.
Khi dịch chuyển B theo phương AB ra xa A một khoảng x ta có: $M{B}’-MA=\left( k+0,5 \right)\lambda $.
$\Rightarrow M{B}’=4,2+1,6\left( k+0,5 \right)$.
Khi đó $M{B}’=9,8cm$.
Lại có: $\cos \widehat{MBA}=\frac{24}{25}\Rightarrow \cos \widehat{MB{B}’}=\frac{-24}{25}$.
Khi đó ${{x}^{2}}+{{9}^{2}}+2.x.9.\frac{24}{25}=9,{{8}^{2}}\Rightarrow x=0,83cm$. Chọn C.
| Bài tập 10: [Trích đề thi chuyên Lê Hồng Phong – Nam Định]. Ở mặt thoáng của một chất lỏng có hai nguồn kết hợp A và B dao động điều hòa cùng pha với nhau và theo phương thẳng đứng. Biết tốc độ truyền sóng không đổi trong quá trình lan truyền, bước sóng do mỗi nguồn phát ra bằng 12 cm. Khoảng cách ngắn nhất giữa hai điểm dao động với biên độ cực đại nằm trên đoạn thẳng AB là:
A. 9 cm B. 12 cm C. 6 cm D. 3 cm |
Lời giải chi tiết:
Gọi M là điểm trên AB dao động với biên độ cực đại.
Khi đó $\left\{ \begin{array}{} MA+MB=AB \\ {} MA-MB=k\lambda \\ \end{array} \right.\Rightarrow MA=\frac{AB+k\lambda }{2}$.
Khoảng cách ngắn nhất giữa hai điểm dao động với biên độ cực đại là: $\Delta d=\frac{\lambda }{2}=6cm$. Chọn C.
| Bài tập 11: [Trích đề thi chuyên Thoại Ngọc Hầu – An Giang]. Hai nguồn sóng kết hợp cùng pha A và B trên mặt nước có tần số 15 Hz. Tại điểm M trên mặt nước cách các nguồn đoạn 14,5 cm và 17,5 cm có biên độ cực đại. Giữa M và đường trung trực của AB có hai dãy cực đại khác. Vận tốc truyền sóng trên mặt nước là:
A. 22,5 cm/s B. 15 cm/s C. 5 cm/s D. 20 cm/s |
Lời giải chi tiết:
Giữa M và đường trung trực của AB có hai dãy cực đại khác nên M thuộc cực đại số 3.
Khi đó ${{d}_{1}}-{{d}_{2}}=3\lambda \Rightarrow \lambda =1cm\Rightarrow v=f\lambda =15cm/s$. Chọn B.
| Bài tập 12: Trong một thí nghiệm về giao thoa sóng trên mặt nước, hai nguồn kết hợp A, B dao động với tần số f = 14 Hz và dao động cùng pha. Tại điểm M cách nguồn A, B những khoảng ${{d}_{1}}=19cm$, ${{d}_{2}}=21cm$, sóng có biên độ cực đại. Giữa M và đường trung trực của AB chỉ có duy nhất một cực đại. Tốc độ truyền sóng trên mặt nước có giá trị là
A. v = 28 m/s B. v = 7 cm/s C. v = 14 cm/s D. v = 56 cm/s |
Lời giải chi tiết:
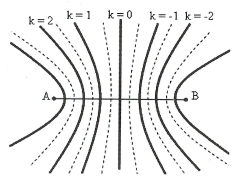
Do 2 nguồn dao động cùng pha và điểm M dao động với biên độ cực đại. Suy ra ${{d}_{2}}-{{d}_{1}}=2=k\lambda $. Giữa M và trung trực của AB có 1 dãy cực đại khác nên M thuộc vân cực đại thứ 2 suy ra k = 2.
Khi đó $\lambda =1cm$.
Tốc độ truyền sóng là $v=f.\lambda =14cm/s$. Chọn B.
| Bài tập 13: Trong thí nghiệm giao thoa sóng, hai nguồn kết hợp A, B dao động ngược pha với cùng tần số $f=15$ Hz. Tại điểm M cách nguồn A, B những khoảng ${{d}_{1}}=22cm,{{d}_{2}}=25cm$, sóng có biên độ cực đại. Giữa M và đường trung trực của AB có hai đường dao động với biên độ cực tiểu. Tốc độ truyền sóng trên mặt nước có giá trị là
A. v = 24 m/s B. v = 22,5 cm/s C. v = 15 cm/s D. v = 30 cm/s |
Lời giải chi tiết:
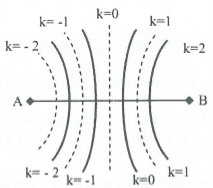
Do 2 nguồn dao động ngược pha và điểm M dao động với biên độ cực đại. Suy ra ${{d}_{1}}-{{d}_{2}}=-3=\left( k+\frac{1}{2} \right)\lambda $. Giữa M và trung trực của AB có 2 dãy cực tiểu nên M thuộc vân cực đại thứ 2 suy ra $k=-2$.
Khi đó $-3\left( -2+0,5 \right)\lambda \Rightarrow \lambda =2cm$.
Vận tốc truyền sóng là $v=f.\lambda =30cm/s$. Chọn D.
| Bài tập 14: Sóng trên mặt nước tạo thành do 2 nguồn kết hợp A và M dao động với tần số 15 Hz. Người ta thấy sóng có biên độ cực đại thứ nhất kể từ đường trung trực của AM tại những điểm có hiệu khoảng cách từ A và M bằng 2 cm. Tính tốc độ truyền sóng trên mặt nước
A. 13 cm/s B. 15 cm/s C. 30 cm/s D. 45 cm/s |
Lời giải chi tiết:
Ta có: ${{d}_{1}}-{{d}_{2}}=k.\lambda $. Biên độ cực đại thứ nhất kể từ đường trung trực của AM
$\Rightarrow k=1\Rightarrow \lambda =2\Rightarrow v=f.\lambda =30cm/s$. Chọn C.
| Bài tập 15: Trong thí nghiệm giao thoa ánh sáng trên mặt nước hai nguồn kết hợp A, B dao động cùng pha với tần số f = 16 Hz tại M cách các nguồn những khoảng 30 cm và 25,5 cm thì dao động với biên động cực đại, giữa M và đường trung trực của AB có 2 dãy cực đại khác. Tốc độ truyền sóng bằng:
A. 13 cm/s B. 26 cm/s C. 52 cm/s D. 24 cm/s |
Lời giải chi tiết:
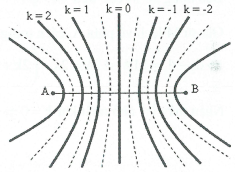
Do 2 nguồn cùng pha và điểm M dao động với biên độ cực đại.
Do đó ${{d}_{1}}-{{d}_{2}}=4,5=k\lambda $. Giữa M và trung trực của AB có 2 dãy cực đại khác nên M thuộc vân cực đại thứ 3 suy ra k = 3.
Khi đó $4,5=3\lambda \Rightarrow \lambda =1,5$cm.
Vận tốc truyền sóng là $v=f.\lambda =24cm/s$. Chọn D.
| Bài tập 16: Hai nguồn sóng kết hợp A và B dao động theo phương trình ${{u}_{A}}={{a}_{1}}\cos \left( \omega t \right)$ và ${{u}_{B}}={{a}_{2}}\cos \left( \omega t+\varphi \right)$. Trên đường thẳng nối hai nguồn, điểm M dao động với biên độ cực tiểu gần trung trực của AB nhất, cách trung trực $\lambda /8$ và lệch về phía A. Giá trị của $\varphi $ có thể bằng
A. $\frac{\pi }{3}$ B. $-\frac{\pi }{3}$ C. $\frac{\pi }{2}$ D. $-\frac{\pi }{2}$ |
Lời giải chi tiết:
M là điểm cực tiểu gần trung trực của AB nhất cách trung trực $\frac{\lambda }{8}$ và lệch về phía A
Ta có $MB-MA=\frac{AB}{2}+\frac{\lambda }{8}-\left( \frac{AB}{2}-\frac{\lambda }{8} \right)=\frac{\lambda }{4}\Rightarrow \left( k+0,5 \right)\lambda +\frac{\varphi \lambda }{2\pi }=\frac{\lambda }{4}\Leftrightarrow \varphi =2\pi \left( -k-\frac{1}{4} \right)$.
Với $k=0\Rightarrow \varphi =-\frac{\pi }{2}\left( ra\text{d} \right)$. Chọn D.
| Bài tập 17: Hai nguồn sóng kết hợp A và B dao động theo phương trình ${{u}_{A}}={{a}_{1}}\cos \left( 100\pi t \right)$cm và ${{u}_{B}}={{a}_{2}}\cos \left( 100\pi t+\frac{\pi }{3} \right)$cm. Điểm M cách các nguồn A, B lần lượt 24 cm và 11 cm có biên độ dao động cực đại. Biết rằng, giữa M và trung trực của AB có 2 cực đại khác. Tính tốc độ truyền sóng?
A. 214,6 cm/s B. 144,6 cm/s C. 123,4 cm/s D. 229,4 cm/s |
Lời giải chi tiết:
Giữa M và trung trực M có 2 cực đại khác $\Rightarrow $ M là cực đại thứ 3
$\Rightarrow AM-MB=\frac{{{\varphi }_{1}}-{{\varphi }_{2}}}{2\pi }\lambda +k\lambda {} \Leftrightarrow 13=-\frac{\lambda }{6}+3\lambda \Leftrightarrow \lambda =4,59cm\Rightarrow v=\frac{\lambda }{T}=229,41\left( cm/s \right)$. Chọn D.
| Bài tập 18: Hai nguồn sóng kết hợp A và B dao động theo phương trình ${{u}_{A}}={{a}_{1}}\cos \left( \omega t \right)$ và ${{u}_{B}}={{a}_{2}}\cos \left( \omega t+\varphi \right)$. Trên đường thẳng nối hai nguồn, điểm M dao động với biên độ cực tiểu gần trung trực của AB nhất, cách trung trực $\lambda /6$ và lệch về phía A. Giá trị của $\varphi $ có thể bằng
A. $\frac{\pi }{3}$ B. $-\frac{\pi }{3}$ C. $\frac{\pi }{2}$ D. $-\frac{\pi }{2}$ |
Lời giải chi tiết:
Độ lệch pha tại điểm M: $\Delta \varphi ={{\varphi }_{1}}-{{\varphi }_{2}}+\frac{2\pi \left( {{d}_{2}}-{{d}_{1}} \right)}{\lambda }=-\varphi +\frac{2\pi \left( {{d}_{2}}-{{d}_{1}} \right)}{\lambda }$
Dao động tại M cực tiểu $\Leftrightarrow -\varphi +\frac{2\pi \left( {{d}_{2}}-{{d}_{1}} \right)}{\lambda }=\left( 2k+1 \right)\pi \Leftrightarrow {{d}_{2}}-{{d}_{1}}=\left( 2k+1+\frac{\varphi }{\pi } \right)\frac{\lambda }{2}$.
Giả sử M lệch về phía A, cách trung điểm AB một đoạn x
$\Rightarrow {{d}_{2}}-{{d}_{1}}=MB-MA=2\text{x}=\left( 2k+1+\frac{\varphi }{\pi } \right)\frac{\lambda }{2}\Rightarrow x=\left( 2k+1+\frac{\varphi }{\pi } \right)\frac{\lambda }{4}$.
Nhận thấy $\left| x \right|$ nhỏ nhất khi $k=0\Rightarrow {{x}_{\min }}=\left( 1+\frac{\varphi }{\pi } \right)\frac{\lambda }{4}=\frac{\lambda }{6}\Rightarrow \varphi =-\frac{\pi }{3}$. Chọn B.
