BÀI TẬP CON LẮC ĐƠN (CLĐ) VỚI LỰC QUÁN TÍNH, LỰC AC-SI-MÉT CÓ ĐÁP ÁN CHI TIẾT
| Bài tập 1: Một con lắc đơn có chu kì $\text{T = 2s}$khi treo vào thang máy đứng yên. Khi thang máy đi lên nhanh dần đều với gia tốc 2${\text{m}}/{{{\text{s}}^{2}}}\;$thì chu kì dao động của con lắc là (lấy g = 10${\text{m}}/{{{\text{s}}^{2}}}\;$).
A. T=2,24 s. B. T=1,83 s. C. T=1,67 s. D. T=2,5 s |
Lời giải chi tiết:
Thang máy lên nhanh dần đều nên $\overrightarrow{\text{a}}\uparrow \Rightarrow \overrightarrow{{{\text{F}}_{\text{qt}}}}\downarrow .$
Ta có: $\text{{g}’=g + a}\Rightarrow \frac{{\text{{T}’}}}{\text{T}}=\sqrt{\frac{\text{g}}{\text{g + a}}}=\sqrt{\frac{10}{12}}\Rightarrow \text{{T}’}=1,83s.$ Chọn B.
| Bài tập 2: [Trích đề thi đại học năm 2007]. Một con lắc đơn treo ở trần một thang máy. Khi thang máy đứng yên, con lắc dao động điều hòa với chu kì T. Khi thang máy đi lên thằng đứng, chậm dần đều với gia tốc có độ lớn bằng một nửa gia tốc trọng trường tại nơi đặt thang máy thì con lắc dao động điều hòa với chu kỳ $\text{{T}’}$bằng
A. $2\text{T}$. B. $\frac{\text{T}}{2}$. C. $\text{T}\sqrt{2}$. D. $\frac{\text{T}}{\sqrt{2}}$. |
Lời giải chi tiết:
Khi thang máy đứng yên. Chu kì dao động của nó là $\text{T = 2 }\!\!\pi\!\!\text{ }\sqrt{\frac{\ell }{\text{g}}}.$
Khi thang máy đi lên thẳng đứng chậm dần đều $\Rightarrow \overrightarrow{\text{a}}\downarrow \Rightarrow \overrightarrow{{{\text{F}}_{\text{qt}}}}\uparrow \Rightarrow \text{{g}’ = g}-\text{a}$
Khi đó $\text{{g}’ = g}-\frac{\text{g}}{\text{2}}=\frac{\text{g}}{\text{2}}\Rightarrow \frac{{\text{{T}’}}}{\text{T}}=\sqrt{\frac{\text{g}}{{\text{{g}’}}}}=\sqrt{2}\Rightarrow \text{{T}’}=\text{T}\sqrt{2}$. Chọn C.
| Bài tập 3: Một con lắc đơn có chiều dài $\ell $ dao động điều hòa với chu kì T = 1,2s. Người ta cắt bỏ $\text{75}%$ chiều dài của nó rồi đặt trong thang máy đi lên thẳng đứng nhanh dần đều với gia tốc có độ lớn bằng một nửa gia tốc trọng trường tại nơi đặt thang máy thì con lắc dao động điều hòa với chu kì $\text{{T}’}$bằng
A. $\text{{T}’}$=2,94 s. B. $\text{{T}’}$=1,7 s. C. $\text{{T}’}$=0,49 s. D. $\text{{T}’}$=0,85 s. |
Lời giải chi tiết:
Khi thang máy đứng yên. Chu kì dao động của nó là $\text{T = 2 }\!\!\pi\!\!\text{ }\sqrt{\frac{\ell }{\text{g}}}.$
Sau khi cắt bỏ $\text{75}%$ chiều dài ta có: ${\ell }’=0,25\ell .$
Khi thang máy đi lên thẳng đứng nhanh dần đều $\Rightarrow \overrightarrow{\text{a}}\uparrow \Rightarrow \overrightarrow{{{\text{F}}_{\text{qt}}}}\downarrow \Rightarrow \text{{g}’ = g + a=g +}\frac{\text{g}}{\text{2}}=\frac{\text{3g}}{\text{2}}.$
Ta có: $\text{{T}’ = 2 }\!\!\pi\!\!\text{ }\sqrt{\frac{0,25\ell }{\text{1,5g}}}=\sqrt{\frac{0,25}{1,5}}\text{T}=\frac{\text{T}}{\sqrt{6}}=0,49\text{s}.$Chọn C.
| Bài tập 4: [Trích đề thi đại học năm 2011]. Một con lắc đơn được treo vào trần một thang máy. Khi thang máy chuyển động thẳng đứng đi lên nhanh dần đều với gia tốc có độ lớn a thì chu kì dao động điều hòa của con lắc là 2,52 s. Khi thang máy chuyển động thẳng đứng đi lên chậm dần đều với gia tốc cũng có độ lớn a thì chu kì dao động điều hòa của con lắc là 3,15 s. Khi thang máy đứng yên thì chu kì dao động điều hòa của con lắc là
A. 2,84 s. B. 2,96 s. C. 2,61 s. D. 2,78 s. |
Lời giải chi tiết:
Khi thang máy chuyển động thẳng đứng đi lên nhanh dần đều ta có: $\overrightarrow{\text{a}}\uparrow \Rightarrow \overrightarrow{\text{F}}\downarrow .$
Do đó ${{\text{g}}_{1}}\text{ = g + a}\Rightarrow {{\text{T}}_{1}}\text{ = 2 }\!\!\pi\!\!\text{ }\sqrt{\frac{\ell }{\text{g + a}}}.$
Khi thang máy chuyển động thẳng đứng đi lên chậm dần đều ta có: $\overrightarrow{\text{a}}\downarrow \Rightarrow \overrightarrow{\text{F}}\uparrow .$
Do đó ${{\text{g}}_{2}}\text{ = g}-\text{a}\Rightarrow {{\text{T}}_{2}}\text{ = 2 }\!\!\pi\!\!\text{ }\sqrt{\frac{\ell }{\text{g}-\text{a}}}.$
Mặt khác $\text{T = 2 }\!\!\pi\!\!\text{ }\sqrt{\frac{\ell }{\text{g}}}\Rightarrow \frac{2}{{{\text{T}}^{2}}}=\frac{\text{1}}{\text{T}_{1}^{2}}+\frac{\text{1}}{\text{T}_{2}^{2}}=\frac{\text{1}}{\text{4}{{\text{ }\!\!\pi\!\!\text{ }}^{2}}}.\frac{\text{g}}{\ell }\Rightarrow \text{T}=2,78\text{s}\text{.}$Chọn D.
| Bài tập 5: Một con lắc đơn cho chiều dài dây treo là $\ell $ và vật nặng có khối lượng m, khối lượng riêng của vật là $\text{D}=8{\text{g}}/{\text{c}{{\text{m}}^{3}}}\;$. Khi đặt trong chân không con lắc đơn dao động với chu kì T = 2 s. Lấy $\text{g}=9,8{\text{m}}/{{{\text{s}}^{2}}}\;$. Tìm chu kì dao động của con lắc khi nó dao động trong nước. Biết khối lượng riêng của nước là ${{\text{D}}_{\text{n}}}={{10}^{3}}{\text{kg}}/{{{\text{m}}^{3}}}\;$.
A. 2,309 s. B. 2,138 s. C. 1,87 s. D. 1,67 s. |
Lời giải chi tiết:
Lực đẩy Acsimet hướng lên tác dụng lên vật là ${{\text{F}}_{\text{ }\!\!\Alpha\!\!\text{ }}}=\text{DVg}$
Ta có: $\text{{P}’}=\text{P}-{{\text{F}}_{\text{ }\!\!\Alpha\!\!\text{ }}}\Rightarrow \text{{g}’}=\text{g}-\frac{\text{DVg}}{\text{ }\!\!\rho\!\!\text{ V}}=\left( 1-\frac{\text{D}}{\text{ }\!\!\rho\!\!\text{ }} \right)\text{g}\Rightarrow \frac{{\text{{T}’}}}{\text{T}}=\sqrt{\frac{1}{1-\frac{\text{D}}{\text{ }\!\!\rho\!\!\text{ }}}}\Rightarrow \text{{T}’}=\text{T}\sqrt{\frac{1}{1-\frac{\text{D}}{\text{ }\!\!\rho\!\!\text{ }}}}.$
Do đó: $\text{{T}’}=2\sqrt{\frac{1}{1-\frac{{{10}^{3}}}{{{8.10}^{3}}}}}=2,138\text{s}.$Chọn B.
| Bài tập 6: Một con lắc đơn được treo trên trần một toa xe, khi xe chuyển động đều con lắc dao động với chu kì T = 0,5 s, cho $\text{g}=10{\text{m}}/{{{\text{s}}^{2}}}\;$. Khi xe chuyển động nhanh dần đều theo phương ngang với gia tốc $3{\text{m}}/{{{\text{s}}^{2}}}\;$thì con lắc dao động với chu kì là
A. 0,489 s. B. 0,978 s. C. 1,957 s. D. 0,510 s. |
Lời giải chi tiết:
Do con lắc đơn đặt trong xe chạy theo phương ngang nên lực quán tính tác dụng lên vật theo phương nằm ngang. Khi đó $\text{{g}’}=\sqrt{{{\text{g}}^{\text{2}}}+{{\text{a}}^{\text{2}}}}.$
Ta có: $\frac{{\text{{T}’}}}{\text{T}}=\sqrt{\frac{\text{g}}{{\text{{g}’}}}}=\sqrt{\frac{\text{g}}{\sqrt{{{\text{g}}^{\text{2}}}+{{\text{a}}^{\text{2}}}}}}\Rightarrow \text{{T}’}=0,489\text{s}.$Chọn A.
| Bài tập 7: Một con lắc đơn được treo trên trần một toa xe, khi xe chuyển động đều con lắc dao động với chu kì 2 s, khi xe chuyển động nhanh dần đều với gia tốc a thì chu kì dao động của nó là 1,55 s. Lấy $\text{g}=10{\text{m}}/{{{\text{s}}^{2}}}\;$. Gia tốc của xe là
A. $13,3{\text{m}}/{{{\text{s}}^{2}}}\;$. B. $8,15{\text{m}}/{{{\text{s}}^{2}}}\;$. C. $2,90{\text{m}}/{{{\text{s}}^{2}}}\;$. D. $6,68{\text{m}}/{{{\text{s}}^{2}}}\;$. |
Lời giải chi tiết:
Do con lắc đơn đặt trong xe chạy theo phương ngang nên lực quán tính tác dụng lên vật theo phương nằm ngang. Khi đó $\text{{g}’}=\sqrt{{{\text{g}}^{\text{2}}}+{{\text{a}}^{\text{2}}}}.$
Ta có: $\frac{{\text{{T}’}}}{\text{T}}=\sqrt{\frac{\text{g}}{{\text{{g}’}}}}=\sqrt{\frac{\text{g}}{\sqrt{{{\text{g}}^{\text{2}}}+{{\text{a}}^{\text{2}}}}}}=\frac{31}{40}\Rightarrow \frac{{{\text{g}}^{2}}}{{{\text{g}}^{\text{2}}}+{{\text{a}}^{\text{2}}}}\text{=}{{\left( \frac{31}{40} \right)}^{4}}\Leftrightarrow \text{a}=13,3{\text{m}}/{\text{s}}\;.$ Chọn A.
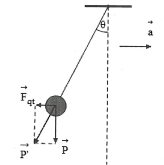
Bài tập 8: Một con lắc đơn có chu kì dao động T = 2 s. Nếu trong con lắc vào trần một toa xe đang chuyển động nhanh dần đều trên mặt đường nằm ngang thì thấy rằng ở vị trí cân bằng mới, dây treo con lắc hợp với phương thằng đứng một góc $\alpha =30{}^\circ $. $\text{g}=10{\text{m}}/{{{\text{s}}^{2}}}\;$. Tìm chu kì dao động mới của con lắc trong toa xe và gia tốc của toa xe?
|
Lời giải chi tiết:
| Ta có: $\text{{P}’}=\frac{\text{P}}{\text{cos }\!\!\theta\!\!\text{ }}\Rightarrow \text{{g}’}=\frac{\text{g}}{\text{cos }\!\!\theta\!\!\text{ }}\Rightarrow \text{{T}’}=\text{2 }\!\!\pi\!\!\text{ }\sqrt{\frac{\ell }{{\text{{g}’}}}}$
$=\text{2 }\!\!\pi\!\!\text{ }\sqrt{\frac{\ell \cos \text{ }\!\!\alpha\!\!\text{ }}{\text{g}}}=\text{T}\sqrt{\cos \text{ }\!\!\alpha\!\!\text{ }}=1,86\text{s}$ Lại có: $\text{tan }\!\!\alpha\!\!\text{ = }\frac{\text{a}}{\text{g}}\Rightarrow \text{a}=5,77{\text{m}}/{{{\text{s}}^{2}}}\;$. Chọn A. |
 |
| Bài tập 9: Một con lắc đơn treo ở trần một thang máy. Khi thang máy đứng yên, con lắc dao động với tần số 0,25 Hz. Khi thang máy đi xuống thằng đứng, chậm dần đều với gia tốc bằng một phần ba gia tốc trọng trường tại nơi đặt thang máy thì con lắc đơn dao động với chu kỳ bằng
A. $\sqrt{3}$s. B. $2\sqrt{3}$s. C. $3\sqrt{2}$s. D. 3$\sqrt{3}$s. |
Lời giải chi tiết:
Khi thang máy đứng yên. Chu kì dao động của nó là $\text{T}=\text{2 }\!\!\pi\!\!\text{ }\sqrt{\frac{\ell }{\text{g}}}=\frac{1}{\text{f}}=4\text{s}\text{.}$
Khi thang máy đi xuống thẳng đứng, chậm dần đều $\overrightarrow{\text{a}}\uparrow \Rightarrow \overrightarrow{{{\text{F}}_{\text{qt}}}}\downarrow \Rightarrow \text{{g}’ = g + a}$
Khi đó $\text{{g}’}=\text{g +}\frac{\text{g}}{3}=\frac{\text{4g}}{3}\Rightarrow \frac{{\text{{T}’}}}{\text{T}}=\sqrt{\frac{\text{g}}{{\text{{g}’}}}}=\frac{3}{4}\Rightarrow \text{{T}’}=\text{T}\frac{\sqrt{3}}{2}=2\sqrt{3}\text{s}\text{.}$Chọn B.
| Bài tập 10: Một tên lửa bắt đầu bay lên theo phương thẳng đứng với gia tốc a = 3g. Trong tên lửa có treo một con lắc đơn dài $\ell $=1m, khi bắt đầu bay thì đồng thời kích thích cho con lắc thực hiện dao động nhỏ. Bỏ qua sự thay đổi gia tốc rơi tự do theo độ cao. Lấy $\text{g}={{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}=10{\text{m}}/{{{\text{s}}^{2}}}\;$. Đến khi đạt độ cao h = 1500 m thì con lắc đã thực hiện được số dao động là
A. 20. B. 14. C. 10. D. 18. |
Lời giải chi tiết:
Chu kì của con lắc là $\text{T = 2 }\!\!\pi\!\!\text{ }\sqrt{\frac{\ell }{\text{g + a}}}=\text{2 }\!\!\pi\!\!\text{ }\sqrt{\frac{\ell }{\text{4g}}}=1$s.
Mặt khác ta có: $\text{h}=\frac{\text{a}{{\text{t}}^{2}}}{2}\Rightarrow \text{t}=\sqrt{\frac{2\text{h}}{\text{a}}}=10$s.
Do đó số dao động vật thực hiện được là $\text{N=}\frac{\text{t}}{\text{T}}=10$. Chọn C.
| Bài tập 11: Một con lắc đơn dao động điều hòa trong một thang máy đứng yên tại nơi có gia tốc $\text{g}=9,8{\text{m}}/{{{\text{s}}^{2}}}\;$với năng lượng dao động 150 mJ. Thang máy bắt đầu chuyển động nhanh dần đều lên trên với gia tốc $2,5{\text{m}}/{{{\text{s}}^{2}}}\;$. Biết thời điểm thang máy bắt đầu chuyển động là lúc con lắc có vận tốc bằng 0. Con lắc sẽ tiếp tục dao động trong thang máy với năng lượng
A. 144 mJ. B. 188mJ. C. 112 mJ. D. 150 mJ. |
Lời giải chi tiết:
Lúc con lắc có $\text{v = 0}$(ở vị trí biên), thang máy bắt đầu chuyển động nhanh dần đều lên trên với gia tốc $2,5{\text{m}}/{{{\text{s}}^{2}}}\;$ $\left( \text{{g}’ = g + a = 12,3}{\text{m}}/{{{\text{s}}^{2}}}\; \right)$thì không làm thay đổi biên độ góc $\left( {{{\text{{ }\!\!\alpha\!\!\text{ }’}}}_{\max }}={{\text{ }\!\!\alpha\!\!\text{ }}_{\max }} \right)$ nên tỉ số cơ năng bằng tỉ số thế năng cực đại và bằng tỉ số gia tốc trọng trường hiệu dụng:
$\frac{{\text{{W}’}}}{\text{W}}=\frac{{{{\text{{W}’}}}_{\text{t}}}}{{{\text{W}}_{\text{t}}}}=\frac{{\text{{g}’}}}{\text{g}}\Rightarrow \text{{W}’}=150.\frac{12,3}{9,8}=188\left( \text{mJ} \right).$ Chọn B.
| Bài tập 12: Một con lắc đơn dao động điều hòa trong một thang máy đứng yên tại nơi có gia tốc $\text{g}=9,8{\text{m}}/{{{\text{s}}^{2}}}\;$với năng lượng dao động 150 mJ. Thang máy bắt đầu chuyển động nhanh dần đều lên trên với gia tốc $2,5{\text{m}}/{{{\text{s}}^{2}}}\;$. Biết thời điểm thang máy bắt đầu chuyển động là lúc con lắc có li độ bằng nửa li độ cực đại. Con lắc sẽ tiếp tục dao động trong thang máy với năng lượng
A. 140,4 mJ. B. 188 mJ. C. 112 mJ. D. 159,6 mJ. |
Lời giải chi tiết:
$\text{{g}’ = g}-\text{a = 7,3}\left( {\text{m}}/{{{\text{s}}^{2}}}\; \right)$
$\Delta {{\text{W}}_{\text{t}}}=\frac{\text{m}\Delta \text{g}\ell }{2}{{\text{a}}^{2}}=\frac{\text{m}\left( \text{{g}’}-\text{g} \right)\ell }{2}\frac{{{\text{a}}^{2}}_{\max }}{4}=\frac{\text{mg}\ell }{2}{{\text{a}}^{2}}_{\max }\left( \frac{{\text{{g}’}}}{\text{g}}-1 \right).\frac{\ell }{4}=-\frac{25}{392}$
$\text{{W}’}=\text{W+}\Delta {{\text{W}}_{\text{t}}}=150-\frac{25}{392}.150=140,4\left( \text{mJ} \right).$ Chọn A.
Bài tập 13: Con lắc đơn treo ở trần một thang máy, đang dao động điều hòa. Khi con lắc về đúng tới vị trí cân bằng thì thang máy bắt đầu chuyển động nhanh dần đều lên trên thì
|
|
Lời giải chi tiết:
Lúc con lắc qua VTCB $\left( \text{ }\!\!\alpha\!\!\text{ }=0 \right)$thang máy bắt đầu chuyển động nhanh dần đều lên trên $\left( \text{{g}’}=\text{g}+\text{a g} \right)$thì không làm thay đổi tốc độ cực đại $\left( {{{\text{{v}’}}}_{\max }}={{\text{v}}_{\max }} \right)$nên không làm thay đổi động năng cực đại, tức là không làm thay đổi cơ năng dao động.
$\frac{\text{m{g}’}\ell }{2}\text{a}_{\max }^{‘2}=\frac{\text{mg}\ell }{2}\text{a}_{\max }^{2}\Rightarrow {{\text{{a}’}}_{\max }}={{\text{a}}_{\max }}\sqrt{\frac{\text{g}}{{\text{{g}’}}}}<{{\text{a}}_{\max }}.$ Chọn A.
| Bài tập 14: Một thang máy đứng yên tại nơi có gia tốc trọng trường $\text{g}=10{\text{m}}/{{{\text{s}}^{2}}}\;$có treo một con lắc đơn và một con lắc lò xo. Kích thích cho các con lắc dao động điều hòa (con lắc lò xo theo phương thẳng đứng) thì thấy chúng đều có tần số góc bằng $10{\text{rad}}/{\text{s}}\;$và biên độ dài đều bằng A = 1cm. Đúng lúc các vật dao động cùng đi qua vị trí cân bằng thì thang máy bắt đầu chuyển động nhanh dần đều xuống phía dưới với gia tốc $2,5{\text{m}}/{{{\text{s}}^{2}}}\;$. Tỉ số biên độ dài giữa con lắc đơn và con lắc lò xo sau khi thang máy chuyển động là
A. 0,53. B. 0,43. C. 1,5. D. 2. |
Lời giải chi tiết:
+) Đối với con lắc lò xo
Tại vị trí cân bằng con lắc lò xo có tốc độ $\text{v = }\!\!\omega\!\!\text{ }\!\!\Alpha\!\!\text{ }$
Khi thang máy đi xuống nhanh dần đều thì vị trí cân bằng của dao động sẽ dịch chuyển lên phía trên vị trí cân bằng cũ một đoạn $\Delta \text{l=}\frac{\mathrm{ma}}{\text{k}}=\frac{\mathrm{a}}{{{\text{ }\!\!\omega\!\!\text{ }}^{2}}}=2,5\text{cm}$
Biên độ dao động mới ${{\text{ }\!\!\Alpha\!\!\text{ }}_{1}}=\sqrt{\Delta {{\text{l}}^{2}}+{{\left( \frac{\text{v}}{\text{ }\!\!\omega\!\!\text{ }} \right)}^{2}}}=\frac{\sqrt{29}}{2}\text{cm}$
+)Đối với con lắc đơn, ta xét bài toán tổng quát hơn
Một con lắc đơn đang dao động điều hòa trong thang máy với biên độ góc ${{\text{ }\!\!\alpha\!\!\text{ }}_{\text{0}}}$ tại vị trí con lắc có li độ góc $\text{ }\!\!\alpha\!\!\text{ }$ thì thang máy đi lên (hoặc đi xuống) nhanh dần đều với gia tốc a. Xác định biên độ góc của con lắc sau đó
Một cách hình thức ta xem con lắc chuyển động trong trường trọng lực biểu kiến với gia tốc biểu kiến $\overrightarrow{{{\text{g}}_{\text{bk}}}}=\overrightarrow{\text{g}}-\overrightarrow{\mathrm{a}}$
Định luật bảo toàn cơ năng cho con lắc (với ${{\text{{ }\!\!\alpha\!\!\text{ }’}}_{\text{0}}}$là biên độ góc lúc sau của dao động)
$\frac{1}{2}\text{m}{{\text{v}}^{2}}+\text{m}{{\text{g}}_{\text{bk}}}\text{l}\left( 1-\cos \text{ }\!\!\alpha\!\!\text{ } \right)=\text{m}{{\text{g}}_{\text{bk}}}\text{l}\left( 1-\cos {{{\text{{ }\!\!\alpha\!\!\text{ }’}}}_{\text{0}}} \right)$
Với ${{\text{v}}^{2}}=2\text{gl}\left( \cos \text{ }\!\!\alpha\!\!\text{ }-\cos {{\text{ }\!\!\alpha\!\!\text{ }}_{\text{0}}} \right)$
Trong khai triển gần đúng: $\cos \text{ }\!\!\alpha\!\!\text{ }\approx 1-\frac{{{\text{ }\!\!\alpha\!\!\text{ }}^{2}}}{2}$ ta thu được $\text{g}\left( \frac{\text{ }\!\!\alpha\!\!\text{ }_{0}^{2}}{2}-\frac{{{\text{ }\!\!\alpha\!\!\text{ }}^{2}}}{2} \right)+{{\text{g}}_{\text{bk}}}\frac{{{\text{ }\!\!\alpha\!\!\text{ }}^{2}}}{2}={{\text{g}}_{\text{bk}}}\frac{{{{\text{{ }\!\!\alpha\!\!\text{ }’}}}_{\text{0}}}}{2}$
Rút gọn biểu thức: ${{\text{{ }\!\!\alpha\!\!\text{ }’}}_{\text{0}}}^{2}=\frac{\text{g}}{{{\text{g}}_{\text{bk}}}}\text{ }\!\!\alpha\!\!\text{ }_{0}^{2}+\left( \frac{{{\text{g}}_{\text{bk}}}-\text{g}}{{{\text{g}}_{\text{bk}}}} \right){{\text{ }\!\!\alpha\!\!\text{ }}^{2}}$
Từ phương trình trên ta thấy rằng
+) Nếu thang máy chuyển động có gia tốc tại vị trí biên $\text{ }\!\!\alpha\!\!\text{ }={{\text{ }\!\!\alpha\!\!\text{ }}_{0}}$thì biên độ góc của con lắc không đổi
+) Nếu thang máy chuyển động có gia tốc tại vị trí cân bằng $\text{ }\!\!\alpha\!\!\text{ }=0$thì biên độ góc của con lắc tỉ lệ với căn bậc hai gia tốc trọng trường trong các trường hợp ${{\text{{ }\!\!\alpha\!\!\text{ }’}}_{\text{0}}}^{2}=\frac{\text{g}}{{{\text{g}}_{\text{bk}}}}\text{ }\!\!\alpha\!\!\text{ }_{0}^{2}$
Áp dụng cho bài toán ${{\text{{ }\!\!\alpha\!\!\text{ }’}}_{\text{0}}}^{2}=\frac{\text{g}}{{{\text{g}}_{\text{bk}}}}\text{ }\!\!\alpha\!\!\text{ }_{0}^{2}\Rightarrow {\Alpha }’=\sqrt{\frac{\text{g}}{{{\text{g}}_{\text{bk}}}}}\Alpha =\frac{2}{\sqrt{3}}\text{cm}\Rightarrow \frac{{{\Alpha }’}}{{{\Alpha }_{1}}}\approx 0,43.$ Chọn B.
