BÀI TẬP NĂNG LƯỢNG CON LẮC LÒ XÒ (CLLX) CÓ LỜI GIẢI CHI TIẾT
| Bài tập 1: Một con lắc lò xo dao động điều hoà. Lò xo có độ cứng $k=80N/m$. Khi vật m của con lắc lò xo đang qua vị trí có li độ $x=-2cm$thì thế năng của con lắc là:
A. 32 J. B. 0,032 J. C. 0,016 J. D. 16 J. |
Lời giải chi tiết
Thế năng của con lắc là ${{E}_{t}}=\frac{k{{\text{x}}^{2}}}{2}=0,016$J. Chọn C.
| Bài tập 2: [Trích đề thi THPT QG năm 2017]. Một con lắc lò xo gồm vật nhỏ, đang dao động điều hoà trên mặt phẳng nằm ngang. Động năng của con lắc đạt giá trị cực tiểu khi:
A. lò xo không biến dạng . B. vật có vận tốc cực đại . C. vật đi qua vị trí cân bằng. D. lò xo có chiều dài cực đại. |
Lời giải chi tiết
Ta có: Động năng của con lắc là${{E}_{}}=\frac{1}{2}m{{v}^{2}}$ cực tiểu khi v = 0 vật đi qua VTCB. Chọn C.
| Bài tập 3: Một con lắc lò xo có độ cứng $k=100N/m$. Vật nặng dao động với biên độ $A=20cm$, khi vật đi qua li độ $x=12cm$thì động năng của vật bằng:
A. 1,28J. B. 2,56J. C. 0,72J. D. 1,44J. |
Lời giải chi tiết
Ta có: ${{E}_{}}=E-{{E}_{t}}=\frac{1}{2}k\left( {{A}^{2}}-{{x}^{2}} \right)=1,28$J. Chọn A.
| Bài tập 4: Một con lắc lò xo gồm vật nhỏ có khối lượng m và lò xo có độ cứng 40N/m đang dao động điều hoà với biên độ 5cm. Khi vật đi qua vị trí có li độ 3cm, con lắc lò xo có động năng bằng:
A. 0,024J. B. 0,032J. C. 0,018J. D. 0,050J. |
Lời giải chi tiết
Ta có: ${{E}_{}}=E-{{E}_{t}}=\frac{1}{2}k\left( {{A}^{2}}-{{x}^{2}} \right)=0,032$J. Chọn B.
| Bài tập 5: Con lắc lò xo gồm vật nặng khối lượng 300g, dao động điều hoà trên quỹ đạo dài 20cm. Trong khoảng thời gian 6 phút, vật thực hiện được 720 dao động. Lấy ${{\pi }^{2}}=10$. Mốc thế năng ở vị trí cân bằng. Cơ năng dao động của vật bằng:
A. 0,024J. B. 0,24J. C. 4,8J. D. 0,96J. |
Lời giải chi tiết
Biên độ giao động của vật là: $A=\frac{\ell }{2}=0,1$cm.
Cơ năng của con lắc: $\text{W}=\frac{1}{2}k{{\text{A}}^{2}}=\frac{1}{2}m{{\omega }^{2}}{{A}^{2}}=\frac{1}{2}m{{\left( 2\pi f \right)}^{2}}{{A}^{2}}=\frac{1}{2}m{{\left( 2\pi .\frac{N}{t} \right)}^{2}}{{A}^{2}}$
Thay số ta được: $\text{W=}\frac{1}{2}0,3.{{\left( 2\pi .\frac{720}{6.60} \right)}^{2}}0,{{1}^{2}}=0,24$J. Chọn B.
| Bài tập 6: Một chất điểm dao động điều hoà trên trục Ox nằm ngang với động năng cực đại ${{\text{W}}_{0}}$, lực kéo về có độ lớn cực đại ${{F}_{0}}$. Vào thời điểm lực kéo về có độ lớn bằng một nửa ${{F}_{0}}$ thì động năng của vật bằng:
A. $\frac{2{{W}_{0}}}{3}$. B. $\frac{3{{W}_{0}}}{4}$. C. $\frac{{{\text{W}}_{0}}}{4}$. D. $\frac{{{\text{W}}_{0}}}{2}$. |
Lời giải chi tiết
Độ lớn lực kéo về $F=m\left| a \right|=m{{\omega }^{2}}\left| x \right|=\frac{1}{2}{{F}_{0}}\Leftrightarrow \left| x \right|=\frac{A}{2}.$
Suy ra $\frac{\text{W}}{{{\text{W}}_{0}}}=\frac{{{v}^{2}}}{v_{0}^{2}}=\frac{{{A}^{2}}-{{x}^{2}}}{{{A}^{2}}}=\frac{3}{4}$. Chọn B.
| Bài tập 7: Một con lắc lò xo dao động điều hoà với biên độ A trên mặt phẳng nằm ngang. Khi thế năng của vật gấp đôi động năng thì vận tốc của vật là 10cm/s. Vận tốc cực đại của vật trong quá trình dao động là:
A. ${{v}_{\text{max}}}=10\sqrt{3}cm/s$. B. ${{v}_{\text{max}}}=20cm/s$. C. ${{v}_{\text{max}}}=\frac{20}{\sqrt{3}}cm/s$. D. ${{v}_{\text{max}}}=5\sqrt{6}cm/s$. |
Lời giải chi tiết
Ta có: ${{E}_{}}=\frac{1}{2}{{E}_{t}}\Rightarrow x=\frac{\pm A}{\sqrt{\frac{1}{2}+1}}=\pm A\sqrt{\frac{2}{3}}$
Mặt khác ${{\left( \frac{x}{A} \right)}^{2}}+{{\left( \frac{v}{{{v}_{\text{max}}}} \right)}^{2}}=1\Rightarrow v=\frac{\pm {{v}_{\text{max}}}}{\sqrt{3}}\Rightarrow {{v}_{\text{max}}}=10\sqrt{3}cm/s$. Chọn A.
| Bài tập 8: [Trích đề thi THPT QG năm 2015]. Một con lắc lò xo có khối lượng vật nhỏ là m dao động điều hoà theo phương ngang với phương trình $x=A\cos \omega t$. Mốc thế năng ở vị trí cân bằng. Cơ năng của con lắc là:
A. $\frac{1}{2}m\omega {{A}^{2}}$. B. $m\omega {{A}^{2}}$. C.$\frac{1}{2}m{{\omega }^{2}}{{A}^{2}}$. D. $m{{\omega }^{2}}{{A}^{2}}$. |
Lời giải chi tiết
Cơ năng của con lắc là: $E=\frac{1}{2}k{{\text{A}}^{2}}=\frac{1}{2}m{{\omega }^{2}}{{A}^{2}}$. Chọn C.
| Bài tập 9: [Trích đề thi THPT QG năm 2008]. Một con lắc lò xo dao động điều hoà. Biết lò xo có độ cứng 36N/m và vật nhỏ có khối lượng 100g. Lấy ${{\pi }^{2}}=10$. Động năng của con lắc lò xo biến thiên theo thời gian với tần số:
A. 6Hz. B. 3Hz. C. 12Hz. D. 1Hz. |
Lời giải chi tiết
Ta có: $\omega ‘=2\omega \Rightarrow f’=2f=2.\frac{1}{2\pi }.\sqrt{\frac{k}{m}}=6$(Hz). Chọn A.
| Bài tập 10: [Trích đề thi THPT QG năm 2009]. Một con lắc lò xo có khối lượng vật nhỏ là 50g, con lắc dao động điều hoà theo một trục nằm ngang cố định với phương trình $x=A\cos \omega t$ cứ sau khoảng thời gian 0,05s thì động năng của vật lại bằng nhau. Lấy ${{\pi }^{2}}=10$ lò xo của con lắc có độ cứng bằng:
A. 25 N/m. B. 200 N/m. C. 100 N/m. D. 50 N/m. |
Lời giải chi tiết
Khi động năng bằng thế năng ${{E}_{}}={{E}_{t}}\Rightarrow x=\frac{\pm A}{\sqrt{1+1}}=\frac{\pm A}{\sqrt{2}}$.
Khoảng thời gian 2 lần liên tiếp động năng và thế năng của vật lại bằng nhau là ${{t}_{\left( \frac{A\sqrt{2}}{2}\to \frac{A\sqrt{2}}{2} \right)}}=\frac{T}{8}+\frac{T}{8}=\frac{T}{4}=0,05\Rightarrow T=0,2=2\pi \sqrt{\frac{m}{k}}=50N/m$. Chọn D.
| Bài tập 11: Một con lắc lò xo dao động điều hoà theo phương nằm ngang. Biết rằng khi tốc độ của vật là $48\pi $cm/s thì động năng bằng n lần thế năng, còn khi vật có li độ x=4cm thì thế năng bằng n lần động năng. Chu kỳ dao động của con lắc là:
A. T=0,52 s. B. T=0,6 s. C. T=0,167 s. D. T=0,256 s. |
Lời giải chi tiết
Khi động năng bằng n lần thế năng ta có: $x=\frac{\pm A}{\sqrt{n+1}}\Rightarrow v=\pm \sqrt{\frac{n}{n+1}}{{v}_{\text{max}}}$
Do đó ${{\left( \frac{v}{{{v}_{\text{max}}}} \right)}^{2}}=\frac{n}{n+1}\Rightarrow {{\left( \frac{48\pi }{\omega A} \right)}^{2}}=\frac{n}{n+1}.$
Khi ${{E}_{t}}=n{{E}_{}}\Rightarrow x=\pm \sqrt{\frac{n}{n+1}}A\Rightarrow {{\left( \frac{4}{A} \right)}^{2}}=\frac{n}{n+1}.$
Do đó ${{\left( \frac{48\pi }{\omega A} \right)}^{2}}={{\left( \frac{4}{A} \right)}^{2}}\Rightarrow \omega =12\pi ra\text{d}/s\Rightarrow T=0,167$s Chọn C.
| Bài tập 12: [Trích đề thi THPT QG năm 2017]. Một con lắc lò xo gồm một vật nhỏ có độ cứng 20 N/m dao động điều hoà với chu kỳ 2s. Sau khi pha của dao động là $\frac{\pi }{2}$ thì vận tốc của vật là $-20\sqrt{3}$cm/s. Lấy ${{\pi }^{2}}=10$, khi vật đi qua vị trí có li độ $3\pi $(cm) thì động năng của con lắc là:
A. 0,36J. B. 0,72J. C. 0,03J. D. 0,18J. |
Lời giải chi tiết
Ta có: $\omega =\frac{2\pi }{T}=\pi $(rad/s), Khi $\varphi =\frac{\pi }{2}\Rightarrow v=-\omega A\sin \frac{\pi }{2}=-20\sqrt{3}\Rightarrow A=\frac{20\sqrt{3}}{\pi }$
Khi $x=3\pi \Rightarrow {{E}_{}}=\frac{1}{2}k\left( {{A}^{2}}-{{x}^{2}} \right)=0,03$J. Chọn C.
| Bài tập 13: [Trích đề thi đại học năm 2009]. Một con lắc lò xo nhẹ và vật nhỏ dao động điều hoà theo phương nằm ngang với tần số 10 rad/s. Biết rằng khi động năng và thế năng (mốc ở vị trí cân bằng của vật) bằng nhau thì vận tốc của vật có độ lớn bằng 0,6m/s. Biên độ dao dộng của con lắc là:
A. 12cm. B. $12\sqrt{2}$cm. C. 6cm. D. $6\sqrt{2}$cm. |
Lời giải chi tiết
Ta có khi động năng bằng thế năng: ${{E}_{}}={{E}_{t}}\Rightarrow x=\frac{\pm A}{\sqrt{1+1}}=\frac{\pm A}{\sqrt{2}}$.
Do $\overrightarrow{x}\bot \overrightarrow{v}\Rightarrow {{\left( \frac{x}{A} \right)}^{2}}+{{\left( \frac{v}{{{v}_{\text{max}}}} \right)}^{2}}=1\Rightarrow {{\left( \frac{v}{{{v}_{\text{max}}}} \right)}^{2}}=1-\frac{1}{2}=\frac{1}{2}$.
Do đó ${{v}_{\text{max}}}=\left| v \right|\sqrt{2}=60\sqrt{2}=\omega A\Rightarrow A=6\sqrt{2}$cm. Chọn D.
| Bài tập 14: [Trích đề thi đại học năm 2009]. Vật nhỏ của một con lắc lò xo dao động điều hoà theo phương ngang, mốc thế năng tại vị trí cân bằng. Khi gia tốc của vật có độ lớn bằng một nửa gia tốc cực đại thì tỉ số giữa động năng và thế năng của vật là:
A. $\frac{1}{2}$. B. 3. C. 2. D. $\frac{1}{3}$. |
Lời giải chi tiết
Ta có: Khi $\left| a \right|=\frac{{{a}_{\text{max}}}}{2}\Rightarrow \left| \omega x \right|=\frac{\omega A}{2}\Rightarrow \left| \frac{x}{A} \right|=\frac{1}{2}$
Suy ra $\frac{{{E}_{}}}{{{E}_{t}}}=\frac{\frac{1}{2}k\left( {{A}^{2}}-{{x}^{2}} \right)}{\frac{1}{2}k{{\text{x}}^{2}}}=\frac{{{A}^{2}}-{{x}^{2}}}{{{\text{x}}^{2}}}=\frac{{{\left( 2\text{x} \right)}^{2}}-{{x}^{2}}}{{{x}^{2}}}=3$. Chọn B.
| Bài tập 15: [Trích đề thi đại học năm 2011]. Khi nói về vật dao động điều hoà. Khẳng định nào sau đây là sai:
A. Động năng của vật biến thiên tuần hoàn theo thời gian. B. Lực kéo về tác dụng biến thiên điều hoà theo thời gian. C. Cơ năng của vật biến thiên tuần hoàn theo thời gian. D. Vận tốc của vật bién thiên điều hoà theo thời gian. |
Lời giải chi tiết
Trong dao động điều hoà, cơ năng của vật là hằng số nên C sai. Chọn C.
| Bài tập 16: [Trích đề thi đại học năm 2011]. Dao động của một chất điẻm có khối lượng 100g là tổng hợp của hai dao động điều hoà cùng phương, có phương trình li độ lần lượt là ${{x}_{1}}=5\cos 10t$và ${{x}_{2}}=10\cos 10t$(${{x}_{1}}$ và ${{x}_{2}}$tính bằng cm, t tính bằng s). Mốc thế năng ở vị trí cân bằng. Cơ năng của chất diểm bằng:
A. 225J. B. 0,225J. C.112,5J. D. 0,1125J. |
Lời giải chi tiết
Ta có: $x={{x}_{1}}+{{x}_{2}}=15\cos 10t\Rightarrow E=\frac{1}{2}k{{\text{A}}^{2}}=\frac{1}{2}m{{\omega }^{2}}{{A}^{2}}=0,1125$J. Chọn D.
| Bài tập 17: [Trích đề thi đại học năm 2017]. Một con lắc lò xo dao động theo phương ngang với cơ năng dao động là 1J và lực đàn hồi cực đại là 10N. Mốc thế năng tại vị trí cân bằng. Gọi Q là đầu cố định của lò xo, khoảng thời gian ngắn nhất giữa 2 lần liên tiếp Q chịu tác dụng lực kéo của lò xo có độ lớn là $5\sqrt{3}$(N) là 0,1s. Quãng đường lớn nhất mà vật nhỏ con lắc đi được trong 0,4s là?
A. 60 cm. B. 115 cm. C. 80 cm. D. 40 cm. |
Lời giải chi tiết
Ta có: ${{F}_{\text{max}}}=k\text{A}=10N$, $E=\frac{1}{2}k{{\text{A}}^{2}}=1J\Rightarrow A=\frac{2\text{E}}{{{F}_{\text{max}}}}=20cm\Rightarrow k=50N/m$.
Khi đó: $\left| F \right|=5\sqrt{3}N\Rightarrow \left| x \right|=10\sqrt{3}cm=\frac{A\sqrt{3}}{2}$
Khoảng thời gian ngắn nhất giữa 2 lần $\left| x \right|=\frac{A\sqrt{3}}{2}$ là $\Delta t={{t}_{\left( \frac{A\sqrt{3}}{2}\to A \right)}}+{{t}_{\left( A\to \frac{A\sqrt{3}}{2} \right)}}=\frac{T}{12}+\frac{T}{12}$
Suy ra $\frac{T}{6}=0,1\Rightarrow T=0,6\text{s}$
Lại có: $\frac{0,4}{0,6}=\frac{2T}{3}=\frac{T}{2}+\frac{T}{6}=\frac{T}{2}+\frac{T}{12}+\frac{T}{12}$ suy ra ${{S}_{\text{max}}}=2\text{A+}\frac{A}{2}+\frac{A}{2}=3\text{A}=60cm$. Chọn A.
| Bài tập 18:[Trích đề thi đại học năm 2011]. Một chất điểm dao động điều hoà trên trục Ox với biên độ 10cm, chu kỳ 2s. Mốc thế năng ở vị trí cân bằng. Tốc độ trung bình của chất điểm trong khoảng thời gian ngắn nhất khi chất điểm đi từ vị trí có động năng bằng 3 lần thế năng đến vị trí có động năng bằng $\frac{1}{3}$ lần thế năng là:
A. 26,12 cm/s. B. 21,96 cm/s. C. 7,32 cm/s. D. 14,64 cm/s. |
Lời giải chi tiết
Khi động năng bằng 3 lần thế năng: ${{E}_{}}=3{{E}_{t}}\Rightarrow x=\frac{\pm A}{\sqrt{3+1}}=\frac{\pm A}{2}$
Khi động năng bằng $\frac{1}{3}$ lần thế năng: ${{E}_{}}=\frac{1}{3}{{E}_{t}}\Rightarrow x=\frac{\pm A}{\sqrt{\frac{1}{3}+1}}=\frac{\pm A\sqrt{3}}{2}.$
Suy ra $\Delta {{t}_{\min }}={{t}_{\left( \frac{A}{2}\to \frac{A\sqrt{3}}{2} \right)}}=\frac{T}{6}-\frac{T}{12}=\frac{T}{12}=\frac{1}{6}$(s), $s=\frac{A\sqrt{3}-A}{2}=5\sqrt{3}-5$(cm)
Do đó tốc độ trung bình là $\frac{s}{\Delta t}=21,96$cm/s. Chọn B.
| Bài tập 19:[Trích đề thi THPT QG năm 2016]. Một chất điểm dao động điều hoà có vận tốc cực đại 60 cm/s và gia tốc cực đại là $2\pi $( $m/{{s}^{2}}$). Chọn mốc thế năng tại vị trí cân bằng. Thời điểm ban đầu (t=0), chất điểm có vận tốc 30 cm/s và thế năng đang tăng. Chất điểm có gia tốc $\pi $( $m/{{s}^{2}}$) lần đầu tiên ở thời điểm:
A. 0,35 s. B. 0,15 s. C. 0,10 s. D. 0,25 s. |
Lời giải chi tiết
Ta có: $\omega =\frac{{{a}_{\text{max}}}}{{{v}_{\text{max}}}}=\frac{10}{3}\pi \Rightarrow T=\frac{2\pi }{\omega }=0,6$(s)
Lại có: ${{\left( \frac{v}{{{v}_{\text{max}}}} \right)}^{2}}+{{\left( \frac{x}{A} \right)}^{2}}=1\Rightarrow v=30cm/s=\frac{{{v}_{\text{max}}}}{2}\Rightarrow \left| x \right|=\frac{A\sqrt{3}}{2}.$.
Do $t=0$, ${{E}_{t}}\nearrow \Rightarrow \frac{k{{\text{x}}^{2}}}{2}\nearrow \Rightarrow \left| x \right|\nearrow \xrightarrow{v>0}\left\{ \begin{array}{} x=\frac{A\sqrt{3}}{2} \\ {} v>0 \\ \end{array} \right..$
Khi $a=\pi (m/{{s}^{2}})=\frac{{{a}_{\text{max}}}}{2}\Rightarrow x=-\frac{A}{2}\Rightarrow \Delta t={{t}_{\left( \frac{A\sqrt{3}}{2}\to A \right)}}+{{t}_{\left( A\to \frac{-A}{2} \right)}}=\frac{T}{12}+\frac{T}{4}+\frac{T}{12}=0,25\text{s}$. Chọn D.
| Bài tập 20:[Trích đề thi đại học năm 2014]. Một con lắc lò xo gồm lò xo nhẹ và vật nhỏ có khối lượng 100g đang dao động điều hoà theo phương ngang, mốc tính thế năng tại vị trí cân bằng. Từ thời điểm ${{t}_{1}}=0$ đến ${{t}_{2}}=\frac{\pi }{48}s$, động năng của con lắc tăng từ 0,096J đến giá trị cực đại rồi giảm về 0,064J. Ở thời điểm ${{t}_{2}}$, thế năng của con lắc bằng 0,064J. Biên độ dao động của con lắc là:
A. 5,7 cm. B. 7,0 cm. C. 8,0 cm. D. 3,6 cm. |
Lời giải chi tiết
Tại thời điểm ${{t}_{2}}$có ${{E}_{}}={{E}_{t}}=0,064$J, nên bằng kiến thức đã học ta tính được:
+) Cơ năng của hệ: $E={{E}_{}}+{{E}_{t}}=0,128$J
+) Vật đang qua li độ: ${{x}_{2}}=\pm \frac{A\sqrt{2}}{2}$
Tại thời điểm ${{t}_{1}}=0$ ta có ${{E}_{t1}}=E-{{E}_{1}}=0,032J=\frac{0,128}{4}=\frac{E}{4}$ nên ${{x}_{1}}=\pm \frac{A}{2}$
Thời gian ngắn nhất để vật đi từ ${{x}_{1}}=\pm \frac{A}{2}$ qua gốc O rồi đến ${{x}_{2}}=\pm \frac{A\sqrt{2}}{2}$ sẽ là
$t=\frac{T}{12}+\frac{T}{8}=\frac{5T}{24}$, mặt khác theo đề ra $t={{t}_{2}}-{{t}_{1}}=\frac{\pi }{48}$ nên ta có: $\frac{5T}{24}=\frac{\pi }{48}$
$\Rightarrow T=\frac{1}{10}(s)\Rightarrow \omega =20$rad/s.
Từ biểu thức cơ năng $E=\frac{k{{\text{A}}^{2}}}{2}=\frac{m{{\omega }^{2}}{{A}^{2}}}{2}$ suy ra biên độ:
$A=\sqrt{\frac{2\text{E}}{m{{\omega }^{2}}}}=\sqrt{\frac{2.0,128}{0,1.400}}=0,08m=8cm$. Chọn C.
| Bài tập 21: [Trích đề thi THPT QG năm 2016]. Hai con lắc lò xo giống hệt nhau đặt trên cùng một mặt phẳng nằm ngang. Con lắc thứ nhất và con lắc thứ hai dao động điều hoà cùng pha với biên độ lần lượt là 3A và A. Chọn mốc thế năng của mỗi con lắc tại vị trí cân bằng của nó. Khi động năng của con lắc thứ nhất là 0,72J thì thế năng của con lắc thứ hai là 0,24J. Khi thế năng của con lắc thứ nhất là 0,09J thì động năng của con lắc thứ hai là:
A. 0,31J. B. 0,01J. C. 0,08J. D. 0,32J. |
Lời giải chi tiết
Hai con lắc giống hệt nhau dao động cùng pha nên ${{m}_{1}}={{m}_{2}};{{k}_{1}}={{k}_{2}}\Rightarrow {{\omega }_{1}}={{\omega }_{2}}$
Khi đó ${{x}_{1}}=A\cos \left( \omega t+\varphi \right);{{x}_{2}}=3A\cos \left( \omega t+\varphi \right)\Rightarrow \left\{ \begin{array}{} \frac{{{x}_{1}}}{{{x}_{2}}}=\frac{{{v}_{1}}}{{{v}_{2}}}=\frac{{{A}_{1}}}{{{A}_{2}}}=3 \\ {} \frac{{{E}_{1}}}{{{E}_{2}}}={{\left( \frac{{{A}_{1}}}{{{A}_{2}}} \right)}^{2}}=9 \\ \end{array} \right..$
Do đó $\frac{{{E}_{{{t}_{1}}}}}{{{E}_{{{t}_{2}}}}}={{\left( \frac{{{x}_{1}}}{{{x}_{2}}} \right)}^{2}}=9;\frac{{{E}_{{{}_{1}}}}}{{{E}_{{{}_{2}}}}}={{\left( \frac{{{v}_{1}}}{{{v}_{2}}} \right)}^{2}}=9\Rightarrow \frac{{{E}_{{{t}_{1}}}}}{{{E}_{{{t}_{2}}}}}=\frac{{{E}_{{{}_{1}}}}}{{{E}_{{{}_{2}}}}}=\frac{{{E}_{1}}}{{{E}_{2}}}=9$.
Thời điểm 1 ta có: $\frac{{{E}_{{{t}_{1}}}}}{0,24}=\frac{0,72}{{{E}_{{{}_{2}}}}}=\frac{{{E}_{1}}}{{{E}_{2}}}=9\Rightarrow \left\{ \begin{array}{} {{E}_{1}}=2,88 \\ {} {{E}_{2}}=0,32 \\ \end{array} \right..$
Khi ${{E}_{{{t}_{1}}}}=0,09\Rightarrow {{E}_{{{t}_{2}}}}=0,01\Rightarrow {{E}_{{{}_{2}}}}=0,32-0,01=0,31$J. Chọn A.
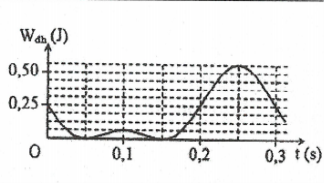
| Bài tập 22: [Trích đề thi THPT QG năm 2017]. Một con lắc lò xo treo vào một điểm cố định ở nơi có gia tốc trọng trường $g={{\pi }^{2}}\left( m/{{s}^{2}} \right)$ cho con lắc dao động điều hoà theo phương thẳng đứng. Hình bên là đồ thị biểu diễn sự phụ thuộc của thế năng đàn hồi ${{\text{W}}_{h}}$ của lò xo vào thời gian t. Khối lượng của con lắc gần nhất với giá trị nào sau đây:
A. 0,65 kg. B. 0,35 kg. C.0,55 kg. D. 0,45 kg. |
Lời giải chi tiết
Dựa vào đồ thị ta suy ra thế năng đàn hồi ở vị trí thấp nhất và cao nhất là $\frac{9}{16}$ và $\frac{1}{16}$ (ứng với mỗi ô là $\frac{0,25}{4}$ mà cao nhất là 9 ô thấp nhất là 1 ô):
Ta có: $\frac{{{\text{W}}_{1}}}{{{\text{W}}_{2}}}=\frac{k{{\left( \Delta \ell +A \right)}^{2}}}{k{{\left( \Delta \ell -A \right)}^{2}}}=9\Rightarrow \Delta \ell +A=3\left( A-\Delta \ell \right)\Rightarrow A=2\Delta \ell \Rightarrow \Delta \ell =\frac{A}{2}.$
Mặt khác thời gian giữa 2 lần liên tiếp ${{\text{W}}_{h}}=0$ là $\Delta t={{t}_{\left( -\frac{A}{2}\to A\to \frac{A}{2} \right)}}=\frac{T}{6}+\frac{T}{6}=\frac{T}{3}=0,1\text{s}$.
Do đó $T=0,3s=2\pi \sqrt{\frac{\Delta \ell }{g}}\Rightarrow \Delta \ell =\frac{9}{400}\left( m \right)\Rightarrow A=\frac{9}{200}\left( m \right).$
Lại có: $\frac{1}{2}k{{\left( \Delta \ell +A \right)}^{2}}=\frac{9}{16}\Rightarrow k=246,91\Rightarrow T=2\pi \sqrt{\frac{m}{k}}\Rightarrow m=0,563$kg. Chọn C.
| Bài tập 23: Hai con lắc lò xo treo thẳng đứng, con lắc thứ nhất có độ cứng k = 50 N/m treo vật nặng có khối lượng m. Con lắc thứ 2 treo vật nặng có khối lượng 2m. Tại thời điểm ban đầu đưa các vật về vị trí lò xo không bị biến dạng rồi thả nhẹ cho hai vật dao động điều hoà. Biết cơ năng của hai con lắc bằng nhau. Độ cứng của con lắc thứ 2 là:
A. 50 N/m. B. 100 N/m. C. 200 N/m. D. 25 N/m. |
Ta có: ${{\text{W}}_{1}}={{\text{W}}_{2}}\Rightarrow \frac{1}{2}{{k}_{1}}A_{1}^{2}=\frac{1}{2}{{k}_{2}}A_{2}^{2}.$
Mặt khác ${{A}_{1}}=\Delta {{\ell }_{1}}=\frac{mg}{{{k}_{1}}};{{A}_{2}}=\Delta {{\ell }_{2}}=\frac{mg}{{{k}_{2}}}\Rightarrow \frac{{{A}_{1}}}{{{A}_{2}}}=\frac{{{k}_{2}}}{2{{k}_{1}}}$
$\Rightarrow \frac{{{\text{W}}_{1}}}{{{\text{W}}_{2}}}=\frac{{{k}_{1}}}{{{k}_{2}}}.{{\left( \frac{{{A}_{1}}}{{{A}_{2}}} \right)}^{2}}=\left( \frac{{{k}_{1}}}{{{k}_{2}}} \right).{{\left( \frac{{{k}_{2}}}{2{{k}_{1}}} \right)}^{2}}=1\Rightarrow \frac{{{k}_{2}}}{4{{k}_{1}}}=1\Rightarrow {{k}_{2}}=4{{k}_{1}}=200N/m.$ Chọn C.
|
Ví dụ 24: [Chuyên ĐH Vinh năm 2013]. Hai con lắc lò xo treo thẳng đứng, vật treo có khối lượng lần lượt là 2m và m. Tại thời điểm ban đầu đưa các vật về vị trí lò xo không bị biến dạng rồi thả nhẹ cho hai vật dao động điều hoà. Biết tỉ số cơ năng dao động của hai con lắc bằng 4. Tỉ số độ cứng của hai con lắc là: A. 4. B. 2. C. 8. D. 1. |
Lời giải
Ta có: ${{A}_{1}}=\Delta {{\ell }_{1}}=\frac{mg}{{{k}_{1}}};{{A}_{2}}=\Delta {{\ell }_{2}}=\frac{mg}{{{k}_{2}}}\Rightarrow \frac{{{A}_{1}}}{{{A}_{2}}}=\frac{2{{k}_{2}}}{{{k}_{1}}}$
$\Rightarrow \frac{{{\text{W}}_{1}}}{{{\text{W}}_{2}}}=\frac{{{k}_{1}}}{{{k}_{2}}}.{{\left( \frac{{{A}_{1}}}{{{A}_{2}}} \right)}^{2}}=\left( \frac{{{k}_{1}}}{{{k}_{2}}} \right).{{\left( \frac{2{{k}_{2}}}{{{k}_{1}}} \right)}^{2}}=4\Rightarrow \frac{{{k}_{2}}}{{{k}_{1}}}=1$. Chọn D.
|
Ví dụ 25: Con lắc lò xo thẳng đứng, lò xo có độ cứng k = 100 N/m, vật nặng có khối lượng m = 1 kg. Nâng vật lên cho lò xo có chiều dài tự nhiên rồi thả nhẹ để con lắc dao động. Bỏ qua mọi lực cản. Khi vật m tới vị trí thấp nhất thì nó tự động được gắn thêm vật ${{m}_{0}}$= 500g một cách nhẹ nhàng. Chọn gốc thế năng là vị trí cân bằng. Lấy g = 10 $m/{{s}^{2}}$. Hỏi năng lương dao động của hệ thay đổi một lượng bằng bao nhiêu? A. Giảm 0,375J. B. Tăng 0,125J. C. Giảm 0,225J. D. Tăng 0,25J. |
Lời giải
Vị trí cân bằng khi có một vật là: $\Delta {{\ell }_{1}}=A=\frac{mg}{k}=10\left( cm \right)$.
Vị trí cân bằng mới gắn thêm vào là: $\Delta {{\ell }_{2}}=\frac{\left( m+{{m}_{0}} \right)g}{k}=15\left( cm \right)$.
Vị trí thấp nhất lò xo dãn $\Delta {{\ell }_{\text{max}}}=2\Delta {{\ell }_{1}}=20\left( cm \right)$.
Do đó biên độ sau khi gắn vật ${{m}_{0}}$vào là $A’=20-15=5\left( cm \right)$.
Năng lượng ban đầu là: ${{E}_{1}}=\frac{1}{2}k{{A}^{2}}=0,5J$.
Năng lượng lúc sau là: ${{E}_{2}}=\frac{1}{2}kA{{‘}^{2}}=0,0125J$.
Độ giảm năng lượng là ${{E}_{1}}-{{E}_{2}}=0,0375.$ Chọn A.
|
Ví dụ 26: [Trích đề thi đại học năm 2012]. Hai chất điểm M và N có cùng khối lượng, dao động điều hoà cùng tần số dọc theo hai đường thẳng song song kề nhau và song song với trục toạ độ Ox. Vị trí cân bằng của M và N đều trên một đường thẳng qua gốc toạ độ và vuông góc với Ox. Biên độ của M là 6 cm, của N là 8 cm. Trong quá trình dao động, khoảng cách lớn nhất giữa M và N theo phương Ox là 10 cm. Mốc thế năng tại vị trí cân bằng. Ở thời điểm mà M có động năng bằng thế năng, tỉ số động năng của m và động năng của N là: A. $\frac{9}{16}$. B. $\frac{4}{3}$. C. $\frac{3}{4}$. D. $\frac{16}{9}$. |
Lời giải
Ta có: ${{x}_{M}}=6\cos \left( \omega t+{{\varphi }_{1}} \right);{{x}_{N}}=8\cos \left( \omega t+{{\varphi }_{2}} \right)\left( cm \right)$.
Suy ra $d=\left| {{x}_{M}}-{{x}_{N}} \right|=\left| 10\cos \left( \omega t+\varphi \right) \right|.$ (Vì ${{d}_{\text{max}}}=10cm$)
Do $A_{1}^{2}+A_{2}^{2}={{10}^{2}}$ nên ${{x}_{M}}\bot {{x}_{N}}$ Khi M có động năng bằng thế năng thì
${{\text{W}}_{M}}=\frac{1}{2}{{\text{W}}_{M}}\Rightarrow {{x}_{M}}=\pm \frac{{{A}_{1}}}{\sqrt{2}}\Rightarrow \left[ \begin{array}{} {{\varphi }_{M}}=\frac{\pi }{4}\Rightarrow {{\varphi }_{N}}=-\frac{\pi }{4} \\ {} {{\varphi }_{M}}=\frac{3\pi }{4}\Rightarrow {{\varphi }_{N}}=\frac{\pi }{4} \\ \end{array} \right.$ nên lúc này N cũng có động năng bằng thế năng. Vậy ${{\text{W}}_{N}}=\frac{1}{2}{{\text{W}}_{N}}$ suy ra $\frac{{{\text{W}}_{M}}}{{{\text{W}}_{N}}}=\frac{{{\text{W}}_{M}}}{{{\text{W}}_{N}}}=\frac{A_{M}^{2}}{A_{N}^{2}}=\frac{9}{16}.$ Chọn A.
|
Ví dụ 27: [Trích đề thi Chuyên Hạ Long – Quảng Ninh 2017]. Một vật nhỏ khối lượng 100g dao động điều hoà với chu kỳ 0,2s và có cơ năng 0,18J. Chọn mốc thế năng tại vị trí cân bằng, lấy ${{\pi }^{2}}=10$ . Tại li độ $3\sqrt{2}$cm , tỉ số động năng và thế năng là: A. 1. B. 7. C. $\frac{5}{3}$. D. $\frac{1}{7}$. |
Lời giải
Cơ năng: $\frac{1}{2}k{{\text{A}}^{2}}=\frac{1}{2}m{{\left( \frac{2\pi }{T} \right)}^{2}}{{A}^{2}}=\frac{1}{2}.0,1.{{\left( \frac{2\pi }{0,2} \right)}^{2}}{{A}^{2}}=0,18\Rightarrow A=6cm$
Tại $x=3\sqrt{2}=\frac{A}{\sqrt{2}}=\frac{A}{\sqrt{1+1}}\Rightarrow {{\text{W}}_{}}={{\text{W}}_{t}}$. Chọn A.
|
Ví dụ 29: Vật dao động điều hoà với vận tốc cực đại bằng 3 m/s và gia tốc cực đại bằng $30\pi \left( m/{{s}^{2}} \right)$ . Lúc t = 0 vật có vận tốc ${{v}_{1}}=-1,5$m/s và thế năng đang tăng. Hỏi sau thời gian ngắn nhất là bao lâu thì vật có gia tốc bằng $-15\pi \left( m/{{s}^{2}} \right)$? A. 0,05s. B. 1/12s. C. 0,10s. D. 0,20s. |
Lời giải
$\omega =\frac{{{a}_{\text{max}}}}{{{v}_{\text{max}}}}=\frac{30\pi }{3}=10\pi $ rad/s $\Rightarrow T=0,2\text{s}$.
Tại thời điểm ban đầu $\left\{ \begin{array}{} v=\frac{-{{v}_{\text{max}}}}{2} \\ {} {{\text{W}}_{t}}=\frac{1}{2}k{{\text{x}}^{2}}\nearrow \Rightarrow \left| x \right|\nearrow \\ \end{array} \right.\Rightarrow \left\{ \begin{array}{} v\text{ }<\text{ }0 \\ {} x=\frac{-A\sqrt{3}}{2} \\ \end{array} \right..$
Khi $a=-15\pi \left( m/{{s}^{2}} \right)=\frac{-{{a}_{\text{max}}}}{2}\Rightarrow x=\frac{A}{2}.$
Thời gian ngắn nhất vật đi từ vị trí ban đầu đến vị trí $x=\frac{A}{2}$ là $\Delta t=\frac{T}{12}+\frac{T}{4}+\frac{T}{12}=\frac{5T}{12}=\frac{1}{12}s.$
Chọn B.
|
Ví dụ 28: [Trích đề thi Chuyên Vĩnh Phúc 2017]. Một chất điểm dao động điều hoà không ma sát trên trục Ox, mốc thế năng ở vị trí cân bằng O; Biết trong quá trình khảo sát chất điểm không đổi chiều chuyển động. Khi vừa rời khỏi vị trí cân bằng môt đoạn s thì động năng của chất điểm là 13,95 mJ, đi tiếp một đoạn s nữa thì động năng của chất điểm chỉ còn 12,60 mJ. Nếu chất điểm đi tiếp một đoạn s nữa thì động năng của chất điểm khi đó bằng: A. 11,25 mJ. B. 10,35mJ. C. 8,95 mJ. D. 6,68 mJ. |
Lời giải
Theo giả thiết ta có: ${{\text{W}}_{{{}_{1}}}}=\text{W}-\frac{1}{2}k{{\text{s}}^{2}}=13,95$ (1) (với W là cơ năng của chất điểm).
Lại có: ${{\text{W}}_{2}}=\text{W}-\frac{1}{2}k{{\left( 2\text{s} \right)}^{2}}=12,6$ (2).
Giải (1) và (2) suy ra $\left\{ \begin{array}{} \text{W=14,4mJ} \\ {} \text{k}{{\text{S}}^{2}}=0,9mJ \\ \end{array} \right.$.
Ta cần tìm: ${{\text{W}}_{}}=\text{W}-\frac{1}{2}k{{\left( \text{3s} \right)}^{2}}=14,4-\frac{9}{4}.0,9=10,35mJ$. Chọn B.
|
Ví dụ 30: Một chất điểm dao động điều hoà không ma sát theo trục Ox với biên độ A, mốc thế năng tại vị trí cân bằng. Khi vừa rời khỏi vị trí cân bằng một đoạn S thì động năng của chất điểm là 9,6 mJ. Đi tiếp một đoạn S nữa thì động năng của chất điểm chỉ còn 8,4 mJ, nếu vật tiếp tục đi một đoạn 2S nữa thì động năng của chất điểm bằng bao nhiêu, biết A > 4S? A. 10 mJ. B. 4,5 mJ. C. 6,4 mJ. D. 3,6 mJ. |
Lời giải
Khi vật đi một đoạn S thì $E={{E}_{t}}+{{E}_{}}\Leftrightarrow \frac{1}{2}k{{\text{A}}^{2}}=\frac{1}{2}k{{S}^{2}}+{{9.6.10}^{-3}}$ (1)
Khi vật đi một đoạn 2S thì $E={{E}_{t}}+{{E}_{}}\Leftrightarrow \frac{1}{2}k{{\text{A}}^{2}}=\frac{1}{2}k4{{S}^{2}}+8,{{4.10}^{-3}}$ (2)
Từ (1) và (2) $\Rightarrow \left\{ \begin{array}{} \frac{1}{2}k{{\text{A}}^{2}}=0,01 \\ {} \frac{1}{2}k{{S}^{2}}={{4.10}^{-4}} \\ \end{array} \right.$.
Khi vật đi một đoạn 4S $\Rightarrow {{E}_{}}=\frac{1}{2}k{{\text{A}}^{2}}-\frac{1}{2}k.16{{S}^{2}}=3,{{6.10}^{-3}}$mJ. Chọn D.
|
Ví dụ 31: Một chất điểm dao động điều hoà không ma sát theo trục Ox với biên độ A, mốc thế năng tại vị trí cân bằng. Khi vừa rời khỏi vị trí cân bằng một đoạn S thì động năng của chất điểm là 10,92 J. Đi tiếp một đoạn S nữa thì động năng của chất điểm chỉ còn 7,68 J, nếu vật tiếp tục đi một đoạn S/2 nữa thì động năng của chất điểm bằng bao nhiêu, biết vật chưa đổi chiều chuyển động? A. 5,75 J. B. 5,50 J. C. 5,25 J. D. 7,25 J. |
Lời giải
Khi vật đi một đoạn S thì $E={{E}_{}}+{{E}_{t}}\Leftrightarrow \frac{1}{2}k{{\text{A}}^{2}}=\frac{1}{2}k{{S}^{2}}+10,09$ (1)
Khi vật đi một đoạn 2S thì $E={{E}_{}}+{{E}_{t}}\Leftrightarrow \frac{1}{2}k{{\text{A}}^{2}}=\frac{1}{2}k4{{S}^{2}}+7,68$ (2)
Từ (1) và (2) $\Rightarrow \left\{ \begin{array}{} \frac{1}{2}k{{\text{A}}^{2}}=12 \\ {} \frac{1}{2}k{{S}^{2}}=1,08 \\ \end{array} \right.$
Khi vật tiếp tục đi một đoạn S/2 nữa thì $\Rightarrow {{E}_{}}=E-{{E}_{t}}\Leftrightarrow {{E}_{}}=\frac{1}{2}k{{\text{A}}^{2}}-\frac{1}{2}k\frac{25}{4}{{S}^{2}}=5,25$J. Chọn C.
|
Ví dụ 32: Một vật dao động điều hoà với biên độ A, đang đi tới vị trí cân bằng ($t$ = 0, vật ở vị trí biên), sau đó một khoảng thời gian $t$ thì vật có thế năng bằng 30J, đi tiếp một khoảng thời gian $3t$ nữa thì chỉ còn cách vị trí cân bằng một khoảng bằng $\frac{A}{7}$. Biết $4t<\frac{T}{4}$ . Hỏi khi tiếp tục đi một thời gian $\frac{T}{4}$ thì thế năng của vật bằng bao nhiêu? A. 33,5 J. B. 0,8 J. C. 45,1 J. D. 0,7 J. |
Lời giải
Ta có $\cos \left( 4\omega t \right)=\pm \frac{1}{7}\Rightarrow \cos \left( \omega t \right)=0,937\Rightarrow \frac{{{E}_{t1}}}{E}={{\left( \frac{x}{A} \right)}^{2}}=0,878\Rightarrow E=34,17$J.
Khi $x=\frac{A}{7}\Rightarrow {{E}_{t}}=0,679J\Rightarrow {{E}_{}}=33,5$J.
Sau khoảng thời gian $\frac{T}{4}$ thì ${{E}_{\left( 2 \right)}}={{E}_{t\left( 3 \right)}}=33,5$J. Chọn A.
|
Ví dụ 33: Một chất điểm dao động điều hoà không ma sát theo trục Ox với biên độ A, mốc thế năng tại vị trí cân bằng. Khi vừa rời khỏi vị trí cân bằng một đoạn S thì động năng của chất điểm là 10,92 J. Đi tiếp một đoạn S nữa thì động năng của chất điểm chỉ còn 7,68 J, nếu vật tiếp tục đi một đoạn $\frac{2S}{3}$ … nữa thì động năng của chất điểm bằng bao nhiêu, biết vật chưa đổi chiều chuyển động? A. 5,75 J. B. 4,32 J. C. 5,25 J. D. 4,84 J. |
Lời giải
Khi vật vừa đi qua vị trí cân bằng đoạn S: ${{E}_{t}}=E-10,92=\frac{1}{2}k{{S}^{2}}.$
Khi vật đi thêm một đoạn S nữa, tương tự ta có: ${{E}_{t}}’=E-7,68=\frac{1}{2}k{{\left( 2S \right)}^{2}}.$
$\Rightarrow \frac{{{E}_{t}}’}{{{E}_{t}}}=\frac{E-7,68}{E-10,92}=4\Rightarrow E=12\left( J \right)\Rightarrow \frac{S}{A}=\sqrt{\frac{E-{{E}_{1}}}{E}}=0,3\Rightarrow \frac{8}{3}S<A.$
Khi vật đi tiếp $\frac{2\text{S}}{3}$: ${{E}_{t3}}={{\left( \frac{8}{3} \right)}^{2}}{{E}_{t1}}={{\left( \frac{8}{3} \right)}^{2}}\left( 12-10,92 \right)=7,68(J)\Rightarrow {{E}_{3}}=12-7,68=4,32(J).$
Chọn B.
|
Ví dụ 34: Một vật dao động điều hoà dọc theo trục Ox, gọi $\Delta t$ là khoảng thời gian giữa hai lần liên tiếp vật có động năng bằng thế năng. Tại thời điểm t vật đi qua trị trí có tốc độ $15\pi \sqrt{3}$ cm/s với độ lớn gia tốc 22,5$m/{{s}^{2}}$, sau đó một khoảng thời gian đúng bằng $\Delta t$ vật đi qua vị trí có độ lớn vận tốc $45\pi $cm/s. Lấy ${{\pi }^{2}}=10$. Quãng đường mà vật có thể đi được tối đa trong 0,1s là: A. $6\sqrt{3}$cm. B. $6\sqrt{6}$cm. C. $6\sqrt{2}$cm. D. 6 cm. |
Lời giải
Khoảng thời gian giữa hai lần liên tiếp vật có động năng bằng thế năng là: $\Delta t=\frac{T}{4}$
Tại thời điểm t: ${{\left( \frac{{{v}_{1}}}{{{v}_{\text{max}}}} \right)}^{2}}+{{\left( \frac{{{a}_{1}}}{{{a}_{\text{max}}}} \right)}^{2}}=1\left( 1 \right)$.
Sau thời gian $\Delta t=\frac{T}{4}\Rightarrow v_{1}^{2}+v_{2}^{2}=v_{\text{max}}^{2}\Leftrightarrow {{v}_{\text{max}}}=30\sqrt{3}\pi (cm/s)$
$\Rightarrow v_{1}^{2}+v_{2}^{2}=v_{\text{max}}^{2}\Leftrightarrow {{v}_{\text{max}}}=30\sqrt{3}\pi (cm/s)$.
(1) $\Leftrightarrow {{\left( \frac{15\pi \sqrt{3}}{30\pi \sqrt{3}} \right)}^{2}}+{{\left( \frac{22,5}{{{a}_{\text{max}}}} \right)}^{2}}=1\Leftrightarrow {{a}_{\text{max}}}=15\sqrt{3}\left( m/{{s}^{2}} \right)$.
Mặt khác $\frac{{{a}_{\text{max}}}}{{{v}_{\text{max}}}}=\omega =5\pi (ra\text{d}/s)\Rightarrow A=6\sqrt{3}cm$.
Quãng đường tối đa mà vật có thể đi trong 0,1s là ${{S}_{\text{max}}}=2\text{A}\sin \frac{\pi \Delta t}{T}=6\sqrt{6}cm.$ Chọn B.