Viết phương trình tiếp tuyến khi biết hệ số góc – cách giải {} bài tập
Phương pháp giải bài toán viết phương trình tiếp tuyến khi biết hệ số góc
Để viết phương trình tiếp tuyến của đồ thị hàm số $y=f\left( x \right)\left( C \right)$ khi biết hệ số góc là k
Giải phương trình $k={f}’\left( x \right)\Rightarrow \left[ \begin{array} {} x={{x}_{01}} \\ {} x={{x}_{02}} \\ {} ………. \\ {} x={{x}_{i}} \\ \end{array} \right.\Rightarrow y\left( {{x}_{i}} \right)\Rightarrow $ Phương trình tiếp tuyến.
Chú ý: Cho 2 đường thẳng ${{d}_{1}}:y={{k}_{1}}x+{{b}_{1}}$ và ${{d}_{2}}:y={{k}_{2}}x+{{b}_{2}}$
Khi đó ${{k}_{1}},{{k}_{2}}$ lần lượt là hệ số góc của các đường thẳng ${{d}_{1}}$ và ${{d}_{2}}$.
▪ Nếu ${{d}_{1}}//{{d}_{2}}\Leftrightarrow \left\{ \begin{array} {} {{k}_{1}}={{k}_{2}} \\ {} {{b}_{1}}\ne {{b}_{2}} \\ \end{array} \right.$
▪ Nếu ${{d}_{1}}\bot {{d}_{2}}\Leftrightarrow {{k}_{1}}.{{k}_{2}}=-1$
▪ Đường thẳng $d:y=k\text{x}+b$ tạo với trục hoành một góc α thì $k=\pm \tan \alpha $.
Bài tập trắc nghiệm viết phương trình tiếp tuyến khi biết hệ số góc có đáp án
| Ví dụ 1: Viết phương trình tiếp tuyến của đồ thị hàm số $y=\frac{x-1}{x-2}$ biết:
a) Tiếp tuyến có hệ số góc là $k=-1$. b) Tiếp tuyến song song với đường thẳng $y=-4\text{x}+5$. c) Tiếp tuyến vuông góc với đường thẳng $y=9\text{x}+2$. |
Lời giải
Ta có: ${y}’=\frac{-1}{{{\left( x-2 \right)}^{2}}}$
a) Do tiếp tuyến có hệ số góc $k=-1$ nên ta có: $\frac{-1}{{{\left( x-2 \right)}^{2}}}=-1\Leftrightarrow \left[ \begin{array} {} x=3 \\ {} x=1 \\ \end{array} \right.$.
Với ${{x}_{0}}=3\Rightarrow {{y}_{0}}=2\Rightarrow $ phương trình tiếp tuyến là: $y=-1\left( x-3 \right)+2=-x+5$.
Với ${{x}_{0}}=1\Rightarrow {{y}_{0}}=0\Rightarrow $ phương trình tiếp tuyến là: $y=-\left( x-1 \right)=-x+1$.
b) Do tiếp tuyến song song với đường thẳng $y=-4\text{x}+2\Rightarrow {{k}_{u}}=-4\Leftrightarrow \frac{-1}{{{\left( x-2 \right)}^{2}}}=-4$
$\Leftrightarrow {{\left( x-2 \right)}^{2}}=\frac{1}{4}\Leftrightarrow \left[ \begin{array} {} x=\frac{5}{2} \\ {} x=\frac{3}{2} \\ \end{array} \right.$
Với ${{x}_{0}}=\frac{5}{2}\Rightarrow {{y}_{0}}=3\Rightarrow $ phương trình tiếp tuyến là: $y=-4\left( x-\frac{5}{2} \right)+3=-4\text{x}+13$
Với ${{x}_{0}}=\frac{3}{2}\Rightarrow {{y}_{0}}=-1\Rightarrow $ phương trình tiếp tuyến là: $y=-4\left( x-\frac{3}{2} \right)-1=-4\text{x}+5$ (loại vì trùng với đường thẳng đã cho)
Vậy phương trình tiếp tuyến là $y=-4\text{x}+13$.
c) Do tiếp tuyến vuông góc với đường thẳng $y=9\text{x}+2$ suy ra ${{k}_{u}}.{{k}_{d}}=-1\Leftrightarrow \frac{-1}{{{\left( x-2 \right)}^{2}}}=\frac{-1}{{{k}_{d}}}=\frac{-1}{9}$
$\Leftrightarrow {{\left( x-2 \right)}^{2}}=9\Leftrightarrow \left[ \begin{array} {} x=5 \\ {} x=-1 \\ \end{array} \right.$.
Với ${{x}_{0}}=5\Rightarrow {{y}_{0}}=\frac{4}{3}\Rightarrow $ phương trình tiếp tuyến là: $y=-\frac{1}{9}\left( x-5 \right)+\frac{4}{3}=\frac{-1}{9}x+\frac{17}{9}$
Với ${{x}_{0}}=-1\Rightarrow {{y}_{0}}=\frac{2}{3}\Rightarrow $ phương trình tiếp tuyến là $y=-\frac{1}{9}\left( x+1 \right)+\frac{2}{3}=\frac{-1}{9}x+\frac{5}{9}$.
| Ví dụ 2: Cho hàm số: $y=\frac{x-1}{x+1}\left( C \right)$
a) Viết phương trình tiếp tuyến của $\left( C \right)$ biết tiếp tuyến vuông góc với đường thẳng $d:x+2y+1=0$. b) Viết phương trình tiếp tuyến của $\left( C \right)$ biết tiếp tuyến song song với đường thẳng ${{d}_{1}}:x-2y-1=0$. |
Lời giải
Gọi $M\left( {{x}_{0}};{{y}_{0}} \right)\in \left( C \right)$ là tiếp điểm.
a) Ta có: $d:y=\frac{-1}{2}x-\frac{1}{2}\Rightarrow {{k}_{d}}=-\frac{1}{2}\Rightarrow {{k}_{u}}=2$. Khi đó ${y}’\left( {{x}_{0}} \right)=\frac{2}{{{\left( {{x}_{0}}+1 \right)}^{2}}}=2\Leftrightarrow \left[ \begin{array} {} {{x}_{0}}=0 \\ {} {{x}_{0}}=-2 \\ \end{array} \right.$
Với ${{x}_{0}}=0\Rightarrow {{y}_{0}}=-1\Rightarrow $ Phương trình tiếp tuyến là: $y=2\text{x}-1$
Với ${{x}_{0}}=-2\Rightarrow {{y}_{0}}=3\Rightarrow $ Phương trình tiếp tuyến là: $y=2\left( x+2 \right)+3=2\text{x}+7$
b) Ta có: ${{d}_{1}}:y=\frac{1}{2}x-\frac{1}{2}$
Do tiếp tuyến song song với đường thẳng $y=20\text{x}+1\Rightarrow {{k}_{n}}={y}’\left( {{x}_{0}} \right)=\frac{2}{{{\left( {{x}_{0}}+1 \right)}^{2}}}=\frac{1}{2}\Leftrightarrow \left[ \begin{array} {} {{x}_{0}}=1 \\ {} {{x}_{0}}=-3 \\ \end{array} \right.$.
Với ${{x}_{0}}=1\Rightarrow {{y}_{0}}=0\Rightarrow $ Phương trình tiếp tuyến là: $y=\frac{1}{2}\left( x-1 \right)\equiv d$ (loại)
Với ${{x}_{0}}=-3\Rightarrow {{y}_{0}}=2\Rightarrow $ Phương trình tiếp tuyến là: $y=\frac{1}{2}\left( x+3 \right)+2=\frac{1}{2}x+\frac{7}{2}$.
| Ví dụ 3: Phương trình tiếp tuyến của đồ thị hàm số $y={{x}^{3}}-3{{\text{x}}^{2}}+2$ có hệ số góc $k=-3$ là:
A. $y=-3\text{x}+3$ B. $y=-3\text{x}+2$ C. $y=-3\text{x}$ D. $y=-3\text{x}-3$ |
Lời giải
Ta có: ${y}’=3{{\text{x}}^{2}}-6\text{x}$. Giải $3{{x}^{2}}-6\text{x}=-3\Leftrightarrow 3{{\left( x-1 \right)}^{2}}=0\Leftrightarrow x=1$.
Với $x=1\Rightarrow y=0\Rightarrow $ Phương trình tiếp tuyến: $y=-3\left( x-1 \right)$. Chọn A.
| Ví dụ 4: Phương trình tiếp tuyến của đồ thị hàm số $y=\frac{x+1}{x-1}$ biết tiếp tuyến song song với đường thẳng $d:2\text{x}+y-7=0$ là:
A. $y=-2\text{x}-3$ B. $y=-2\text{x}+3$ C. $y=-2\text{x}+1$ D. $y=-2\text{x}-1$ |
Lời giải
Ta có: $d:y=-2\text{x}+7;{y}’=\frac{-2}{{{\left( x-1 \right)}^{2}}}=-2\Leftrightarrow \left[ \begin{array} {} x=2 \\ {} x=0 \\ \end{array} \right.$ .
Với $x=2\Rightarrow y=3\Rightarrow $ Phương trình tiếp tuyến: $y=-2\left( x-2 \right)+3=-2\text{x}+7\equiv d$ (loại).
Với $x=0\Rightarrow y=-1\Rightarrow $ Phương trình tiếp tuyến: $y=-2\text{x}-1$. Chọn D.
| Ví dụ 5: Tiếp tuyến của đồ thị hàm số $y={{x}^{4}}+{{x}^{2}}-5$mà vuông góc với đường thẳng $x+6y+1999=0$ là:
A. $y=6\text{x}-9$ B. $y=6\text{x}-6$ C. $y=-6\text{x}+9$ D. $y=-6\text{x}+6$ |
Lời giải
Ta có: $y=\frac{-1}{6}x-\frac{1999}{6}\left( d \right)$. Do tiếp tuyến vuông góc với d nên ${{k}_{d}}.{{k}_{u}}=-1\Rightarrow {{k}_{u}}=\frac{-1}{{{k}_{d}}}=6$.
Giải ${y}’=6\Leftrightarrow 4{{\text{x}}^{3}}+2\text{x}=6\Leftrightarrow x=1\Rightarrow y=-3\Rightarrow $ Phương trình tiếp tuyến là: $y=6\left( x-1 \right)-3=6\text{x}-9$. Chọn A.
| Ví dụ 6: Tiếp tuyến của đồ thị hàm số $y=\frac{2\text{x}-3}{2-x}$ tại điểm có hoành độ $x=-1$ có hệ số góc là:
A. 1 B. 7 C. $\frac{7}{9}$ D. $\frac{1}{9}$ |
Lời giải
Ta có: ${y}’=\frac{7}{{{\left( 2-x \right)}^{2}}}\Rightarrow {y}’\left( -1 \right)=\frac{7}{9}=k$. Chọn C.
| Ví dụ 7: Tiếp tuyến của đồ thị hàm số $y=\frac{x-m}{x+1}$ tại điểm có hoành độ $x=-2$ có hệ số góc là $k=3$. Giá trị của tham số m là:
A. $m=4$ B. $m=-4$ C. $m=-2$ D. $m=2$ |
Lời giải
Ta có: ${y}’=\frac{1+m}{{{\left( x+1 \right)}^{2}}}\Rightarrow {y}’\left( -2 \right)=1+m=3\Leftrightarrow m=2$. Chọn D.
| Ví dụ 8: Tiếp tuyến của đồ thị hàm số $y={{x}^{3}}-4m{{\text{x}}^{2}}+3\text{x}+2$ tại điểm có hoành độ $x=1$ có hệ số góc $k=-2$. Giá trị của tham số m là:
A. $m=1$ B. $m=-1$ C. $m=-2$ D. $m=2$ |
Lời giải
Ta có: ${y}’\left( 1 \right)=3-8m+3=-2\Leftrightarrow m=1$. Chọn A.
| Ví dụ 9: Cho hàm số $y={{x}^{4}}-2{{\text{x}}^{2}}-3$. Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với đường thẳng $y=24\text{x}-1$.
A. $y=24\text{x}-48$ B. $y=24\text{x}-21$ C. $y=24\text{x}-45$ D. $y=24\text{x}-43$ |
Lời giải
Do tiếp tuyến song song với đường thẳng $y=24\text{x}-1$ suy ra ${{k}_{n}}=24$
Khi đó ${y}’=4{{\text{x}}^{3}}-4\text{x}=24\Leftrightarrow x=2\Rightarrow y=5$.
Phương trình tiếp tuyến là: $y=24\left( x-2 \right)+5=24\text{x}-43$. Chọn D.
| Ví dụ 10: Viết phương trình tiếp tuyến của đồ thị hàm số $y={{x}^{3}}+3{{\text{x}}^{2}}-3$ biết tiếp tuyến vuông góc với đường thẳng $y=\frac{-x}{9}+1$.
A. $y=9\text{x}-8$ B. $y=9\text{x}+24$ C. $y=9\text{x}+10$ D. $\left[ \begin{array} {} y=9\text{x}-8 \\ {} y=9\text{x}+24 \\ \end{array} \right.$ |
Lời giải
Do tiếp tuyến vuông góc với $y=\frac{-x}{9}+1$ nên ${{k}_{u}}=\frac{-1}{{{k}_{d}}}=9$
Giải ${y}’=3{{\text{x}}^{2}}+6\text{x}=9\Leftrightarrow \left[ \begin{array} {} x=1 \\ {} x=-3 \\ \end{array} \right.$
Với $x=1\Rightarrow y=1\Rightarrow $ Phương trình tiếp tuyến là: $y=9\left( x-1 \right)+1=9\text{x}-8$
Với $x=-3\Rightarrow y=-3\Rightarrow $ Phương trình tiếp tuyến là: $y=9\left( x+3 \right)-3=9\text{x}+24$
Vậy có 2 phương trình tiếp tuyến là $y=9\text{x}-8;y=9\text{x}+24$. Chọn D.
| Ví dụ 11: Viết phương trình tiếp tuyến của $\left( C \right):y=\frac{3\text{x}+2}{x-1}$ biết tiếp tuyến song song với đường thẳng $5\text{x}+y+2=0$.
A. $y=-5\text{x}-2$ B. $y=-5\text{x}+18$ C. $y=-5\text{x}+10$ D. $y=-5\text{x}+12$ |
Lời giải
Ta có: $d:y=-5\text{x}-2\Rightarrow {{k}_{u}}=-5$. Giải ${y}’=\frac{-5}{{{\left( x-1 \right)}^{2}}}=-5\Leftrightarrow \left[ \begin{array} {} x=0 \\ {} x=2 \\ \end{array} \right.$
Với $x=0\Rightarrow y=-2\Rightarrow $ Phương trình tiếp tuyến là: $y=-5\text{x}-2$ (loại).
Với $x=2\Rightarrow y=8\Rightarrow $ Phương trình tiếp tuyến là: $y=-5\left( x-2 \right)+8=-5\text{x}+18$. Chọn B.
| Ví dụ 12: Cho hàm số $y={{x}^{3}}+2m\text{x}+2\left( C \right)$. Tìm giá trị của tham số m biết tiếp tuyến của $\left( C \right)$ tại điểm có hoành độ $x=-1$ vuông góc với đường thẳng $y=\frac{1}{2}x+3$.
A. $m=-5$ B. $\frac{-5}{2}$ C. $\frac{5}{2}$ D. 5 |
Lời giải
Ta có: ${{k}_{u}}={y}’\left( -1 \right)=3+2m$. Từ gt $\Rightarrow \left( 3+2m \right).\frac{1}{2}=-1\Leftrightarrow 3+2m=-2\Leftrightarrow m=\frac{-5}{2}$. Chọn B.
| Ví dụ 13: Cho hàm số $y=-{{x}^{3}}+2m{{\text{x}}^{2}}+n\left( C \right)$. Tìm tổng $m+n$ biết tiếp tuyến của $\left( C \right)$ tại điểm $A\left( 1;3 \right)$ có hệ số góc là $k=1$.
A. 2 B. 3 C. 4 D. 5 |
Lời giải
Ta có: ${y}’=-3{{\text{x}}^{2}}+4m\text{x}\Rightarrow {y}’\left( 1 \right)=-3+4m=1\Leftrightarrow m=1$
Mặt khác điểm $A\left( 1;3 \right)\in \left( C \right)$ nên $3=-1+2m+n=n+1\Leftrightarrow n=2$. Vậy $m+n=3$. Chọn B.
| Ví dụ 14: Cho hàm số $y=\frac{x+m}{x+n}\left( C \right)$. Biết tiếp tuyến của $\left( C \right)$ tại điểm $A\left( 2;-4 \right)$ song song với đường thẳng $y=-5x+2017$. Vậy giá trị của $2m-n$ là:
A. 2 B. 3 C. 5 D. 7 |
Lời giải
Giải hệ $\left\{ \begin{array} {} -4=\frac{m+2}{n+2} \\ {} {y}’\left( 2 \right)=\frac{n-m}{{{\left( n+2 \right)}^{2}}}=-5 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} m=-4n-10 \\ {} \frac{5n+10}{{{\left( n+2 \right)}^{2}}}=-5 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} m=-4n-10 \\ {} \frac{1}{n+2}=-1 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} n=-3 \\ {} m=2 \\ \end{array} \right.\Rightarrow 2m-n=7$.
Chọn D.
| Ví dụ 15: Cho hàm số $y=\frac{m\text{x}+n}{x-2}\left( C \right)$. Biết $\left( C \right)$ đi qua điểm $A\left( 1;-3 \right)$ và tiếp tuyến của $\left( C \right)$ tại điểm có hoành độ $x=3$ có hệ số góc $k=-5$. Giá trị của biểu thức ${{m}^{2}}+{{n}^{2}}$ bằng:
A. 5 B. 10 C. 13 D. 25 |
Lời giải
Giải hệ $\left\{ \begin{array} {} -3=\frac{m+n}{1-2} \\ {} {y}’\left( 3 \right)=\frac{-2m-n}{{{\left( 3-2 \right)}^{2}}}=-5 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} m+n=3 \\ {} 2m+n=5 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} m=2 \\ {} n=1 \\ \end{array} \right.\Rightarrow {{m}^{2}}+{{n}^{2}}=5$.
Chọn A.
| Ví dụ 16: Cho hàm số $y={{x}^{3}}+m{{\text{x}}^{2}}+n\text{x}\left( C \right)$. Tìm giá trị của ${{m}^{2}}+{{n}^{2}}$ để đồ thị hàm số đi qua điểm $A\left( -1;5 \right)$ và tiếp tuyến tại điểm có hoành độ $x=1$ vuông góc với đường thẳng $y=\frac{-1}{3}x+2$.
A. 5 B. 10 C. 20 D. 25 |
Lời giải
Giải hệ $\left\{ \begin{array} {} 5=-1+m-n \\ {} {y}’\left( 1 \right).\frac{-1}{3}=-1 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} m-n=6 \\ {} \left( 3+2m+n \right)=3 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} m=2 \\ {} n=-4 \\ \end{array} \right.\Rightarrow {{m}^{2}}+{{n}^{2}}=20$. Chọn C.
| Ví dụ 17: Tìm tất cả các giá trị của tham số m để có 2 tiếp tuyến của đồ thị hàm số $y={{x}^{3}}+3m{{\text{x}}^{2}}+2$ có cùng hệ số góc $k=-3$.
A. $-1<m<1$ B. $-1\le m\le 1$ C. $\left[ \begin{array} {} m>1 \\ {} m<-1 \\ \end{array} \right.$ D. $m=\pm 1$ |
Lời giải
Để có 2 tiếp tuyến thì phải có 2 tiếp điểm phân biệt. Giả sử hoành độ tiếp điểm là $x=a$.
Khi đó ta có: ${y}’\left( a \right)=3{{\text{a}}^{2}}+6ma=-3\Leftrightarrow {{a}^{2}}+2ma+1=0$.
Đk có 2 tiếp tuyến có cùng hệ số góc $k=-3$ là: ${{\Delta }_{\left( 1 \right)}}={{m}^{2}}-1>0\Leftrightarrow \left[ \begin{array} {} m>1 \\ {} m<-1 \\ \end{array} \right.$. Chọn C.
| Ví dụ 18: Gọi d là tiếp tuyến có hệ số góc nhỏ nhất của đồ thị hàm số $y=\frac{2}{3}{{x}^{3}}-4{{\text{x}}^{2}}+9\text{x}-11$. Đường thẳng d đi qua điểm nào dưới đây?
A. $M\left( -5;\frac{2}{3} \right)$ B. $P\left( 5;-\frac{2}{3} \right)$ C. $N\left( 2;-\frac{5}{3} \right)$ D. $Q\left( -2;\frac{5}{3} \right)$ |
Lời giải
Ta có $y=\frac{2}{3}{{x}^{3}}-4{{\text{x}}^{2}}+9\text{x}-11\xrightarrow{{}}{y}’=2{{\text{x}}^{2}}-8\text{x}+9,\forall x\in \mathbb{R}$.
Hệ số góc của tiếp tuyến d của đồ thị hàm số tại $M\left( {{x}_{0}};{{y}_{0}} \right)$ là $k={y}’\left( {{x}_{0}} \right)=2\text{x}_{0}^{2}-8{{\text{x}}_{0}}+9$.
Mặt khác $2\text{x}_{0}^{2}-8{{\text{x}}_{0}}+9=2\left( x_{0}^{2}-4{{\text{x}}_{0}}+4 \right)+1=2{{\left( {{x}_{0}}-2 \right)}^{2}}+1\ge 1\Rightarrow {{k}_{\min }}=1$.
Dấu bằng xảy ra khi ${{\left( {{x}_{0}}-2 \right)}^{2}}=0\Leftrightarrow {{x}_{0}}=2\Rightarrow {{y}_{0}}=-\frac{11}{3}$.
Vậy phương trình d là $y+\frac{11}{3}=x-2\Leftrightarrow y=x-\frac{17}{3}\Rightarrow P\left( 5;-\frac{2}{3} \right)\in d$. Chọn B.
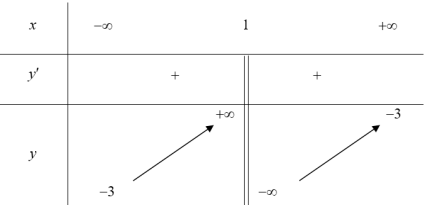
| Ví dụ 19: Cho hàm số $y=\frac{ax+b}{cx-1}\left( C \right)$ có bảng biến thiên như hình vẽ. Biết tiếp tuyến của $\left( C \right)$ tại giao điểm của $\left( C \right)$ với trục tung song song với đường thẳng $y=2\text{x}+2018$.
Giá trị của biể thức $T=a+2b+3c$ là: A. $T=3$ B. $T=1$ C. $T=3$ D. $T=2$ |
Lời giải
Do đồ thị hàm số có tiệm cận đứng $x=1$ và tiệm cận ngang $y=-3$
Do đó hàm số có dạng: $y=\frac{-3\text{x}+b}{x-1}\Rightarrow {y}’=\frac{3-b}{{{\left( x-1 \right)}^{2}}}\Rightarrow {y}’\left( 0 \right)=3-b$
Do tiếp tuyến song song với đường thẳng $y=2\text{x}+2018\Rightarrow 3-b=2\Leftrightarrow b=1$.
Vậy $a=-3;b=1;c=1\Rightarrow T=2$. Chọn D.
| Ví dụ 20: Cho hàm số $y=\frac{x+4}{x-3}\left( C \right)$. Điểm $M\left( {{x}_{0}};{{y}_{0}} \right)$ (với ${{y}_{0}}>0$) thuộc sao $\left( C \right)$ cho tiếp tuyến tại M cắt các trục Ox, Oy lần lượt tại A và B sao cho $AB=5.OA\sqrt{2}$. Giá trị của $2{{\text{x}}_{0}}+{{y}_{0}}$ là:
A. 16 B. 17 C. 18 D. 19 |
Lời giải
Ta có: $\Delta OAB$ vuông tại O ta có: $\tan \widehat{BAO}=\frac{OB}{OA}=\frac{\sqrt{A{{B}^{2}}-O{{A}^{2}}}}{OA}=7$
Gọi k là hệ số góc của tiếp tuyến ta có: $k=\pm 7$.
Gọi $M\left( {{x}_{0}};\frac{{{x}_{0}}+4}{{{x}_{0}}-3} \right)\Rightarrow {y}’\left( {{x}_{0}} \right)=\frac{-7}{{{\left( {{x}_{0}}-3 \right)}^{2}}}=\pm 7\Leftrightarrow {{\left( {{x}_{0}}-3 \right)}^{2}}=1\Leftrightarrow \left[ \begin{array} {} {{x}_{0}}=4 \\ {} {{x}_{0}}=2 \\ \end{array} \right.$
Suy ra $M\left( 4;8 \right)\Rightarrow T=16$. Chọn A.