Bài tập nhận dạng đồ thị hàm số phân thức có đáp án
Dưới đây là một số bài tập trắc nghiệm nhận dạng đồ thị hàm số bậc nhất trên bậc nhất có đáp án chi tiết
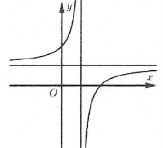
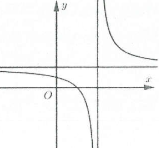
| Bài tập 1: Đường cong hình bên là đồ thị của một hàm số nào trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây.
Hỏi hàm số đó là hàm số nào? A. $y=\frac{x+1}{x-1}$. B. $y=\frac{x-2}{x-1}$. C. $y=\frac{2x-1}{x-1}$. D. $y=\frac{x-3}{x-2}$. |
Lời giải chi tiết
Dựa vào đồ thị hàm số ta thấy đồ thị hàm số có tiệm cận đứng là $x=1$ và tiệm cận ngang là $y=1$ do vậy ta loại hai đáp án là C và D.
Xét đáp án A có $y=\frac{x+1}{x-1}\Rightarrow {y}’=\frac{-2}{{{\left( x-1 \right)}^{2}}}<0$ nên hàm số nghịch biến. Chọn B.
Cách 2: Dựa vào giao điểm của đồ thị hàm số với các trục tọa độ để loại đáp án A.
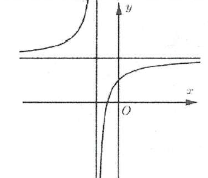
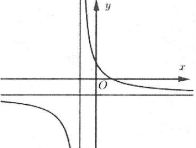
| Bài tập 2: Đường cong hình bên là đồ thị của một hàm số nào trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây.
Hỏi hàm số đó là hàm số nào? A. $y=\frac{2x}{x+1}$. B. $y=\frac{2x+3}{x+1}$. C. $y=\frac{x+2}{x+1}$. D. $y=\frac{2x+1}{x+1}$. |
Lời giải chi tiết
Đồ thị hàm số nhận các đường thẳng $x=-1$ và $y=2$ là đường tiệm cận nên loại đáp án C.
Hàm số đã cho đồng biến trên từng khoảng xác định. Mặt khác với $y=\frac{2x+3}{x+1}$ có ${y}’=\frac{-1}{{{\left( x+1 \right)}^{2}}}<0$
Loại đáp án B. Đồ thị hàm số không đi qua gốc tọa độ nên loại A. Chọn D.
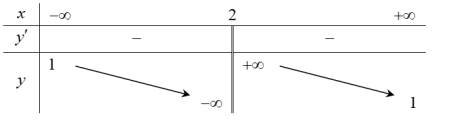
| Bài tập 3: Cho hàm số $y=\frac{ax+b}{cx+d}$ có bảng biến thiên như hình vẽ bên. Hỏi hàm số đã cho là hàm số nào?
A. $y=\frac{x-3}{x-2}$. B. $y=\frac{x+3}{x-2}$. C. $y=\frac{x-3}{x+2}$. D. $y=\frac{-x+3}{x+2}$. |
Lời giải chi tiết
Dựa vào bảng biến thiên ta thấy:
Đồ thị hàm số nhận các đường thẳng $x=2$ và tiệm cận ngang $y=1$ (loại đáp án C và D).
Hàm số đã cho nghịch biến trên mỗi khoảng xác định.
Xét hàm số $y=\frac{x-3}{x-2}\Rightarrow {y}’=\frac{1}{{{\left( x-2 \right)}^{2}}}\Rightarrow $Hàm số đồng biến trên mỗi khoảng xác định nên ta loại đáp án A. Chọn B.
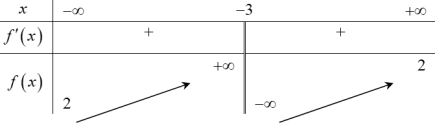
| Bài tập 4: Cho hàm số $y=\frac{ax+b}{cx+d}$ có bảng biến thiên như hình vẽ bên. Hỏi hàm số đã cho là hàm số nào?
A. $y=\frac{2x+1}{x-3}$. B. $y=\frac{2-x}{x+3}$. C. $y=\frac{2x+7}{x+3}$. D. $y=\frac{2x-1}{x+3}$. |
Lời giải chi tiết
Dựa vào bảng biến thiên ta thấy:
Đồ thị hàm số nhận các đường thẳng $x=-3$ và tiệm cận ngang $y=1$ (loại đáp án A và B).
Hàm số đã cho đồng biến trên mỗi khoảng xác định.
Xét hàm số $y=\frac{2x+7}{x+3}\Rightarrow {y}’=\frac{-1}{{{\left( x+3 \right)}^{2}}}<0\left( \forall x\ne -3 \right)\Rightarrow $ Hàm số đồng biến trên mỗi khoảng xác định nên ta loại đáp án C. Chọn D.
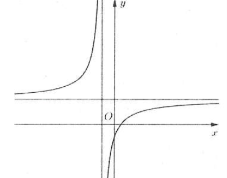
| Bài tập 5: Cho hàm số $y=\frac{ax+b}{cx+d}$ có đồ thị như hình vẽ bên.
Khẳng định nào sau đây đúng? A. $a>0,\,b>0,\,c>0,\,d<0$. B. $a>0,\,b0,\,d<0$. C. $a>0,\,b<0,\,c0$. D. $a0,\,c0$.. |
Lời giải chi tiết
Đồ thị hàm số có tiệm cận đứng: $x=-\frac{d}{c}$ và tiệm cận ngang: $y=\frac{a}{c}$ ta có: $\left\{ \begin{array} {} -\frac{d}{c}>0 \\ {} \frac{a}{c}>0 \\ \end{array} \right.\Rightarrow \left\{ \begin{array} {} cd0 \\ \end{array} \right.$
Đồ thị cắt $Ox$ tại $\left( \frac{-b}{a};0 \right)$, cắt $Oy$ tại $\left( 0;\frac{d}{d} \right)\Rightarrow \left\{ \begin{array} {} \frac{-b}{a}>0 \\ {} \frac{b}{d}>0 \\ \end{array} \right.\Rightarrow \left\{ \begin{array} {} ab0 \\ \end{array} \right.$
Với $a>0\Rightarrow b0;d<0$.
Với $a0;c0$.
Do đó $a>0,\,b>0,\,c>0,\,d<0$. Chọn B.
| Bài tập 6: Cho hàm số $y=\frac{ax+b}{cx+d}$ có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?
A. $ab>0,\,bc0$. B. $ab>0,\,bc<0,\,ad<0$. C. $ab0,\,ad<0$. D. $ab<0,\,bc<0,\,ad<0$. |
Lời giải chi tiết
Đồ thị hàm số có tiệm cận đứng: $x=-\frac{d}{c}$ và tiệm cận ngang: $y=\frac{a}{c}$ ta có: $\left\{ \begin{array} {} -\frac{d}{c}<0 \\ {} \frac{a}{c}0 \\ {} ac0 \\ {} \frac{b}{d}>0 \\ \end{array} \right.\Rightarrow \left\{ \begin{array} {} ab0 \\ \end{array} \right.$
Chọn $a>0\Rightarrow b<0,c<0,d<0$ (vì $y=\frac{ax+b}{cx+d}=\frac{-ax-b}{-cx-d}$) suy ra $ab0,\,ad<0$. Chọn C.
| Bài tập 7: Cho hàm số $y=\frac{ax+b}{cx+d}$ có đồ thị như hình vẽ bên.
Khẳng định nào sau đây đúng? A. $\left\{ \begin{array} {} ad<0 \\ {} bc<0 \\ \end{array} \right.$. B. $\left\{ \begin{array} {} ad0 \\ \end{array} \right.$. C. $\left\{ \begin{array} {} ad>0 \\ {} bc<0 \\ \end{array} \right.$. D. $\left\{ \begin{array} {} ad>0 \\ {} bc>0 \\ \end{array} \right.$. |
Lời giải chi tiết
Dựa vào đồ thị hàm số, ta thấy:
Đồ thị hàm số cắt trục $Ox$ tại điểm có hoành độ dương nên $x=\frac{-b}{a}>0$.
Đồ thị hàm số cắt trục $Oy$ tại điểm có tung độ âm nên $y=\frac{-b}{d}<0$.
Đồ thị hàm số nhận $x=\frac{-d}{c}0$ làm tiệm cậm ngang.
Chọn $a>0$ suy ra $b0,d>0\Rightarrow \left\{ \begin{array} {} ad>0 \\ {} bc<0 \\ \end{array} \right.$. Chọn C.
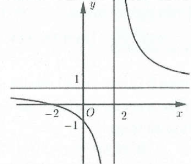
| Bài tập 8: Tìm $a,b,c$ để hàm số $y=\frac{2}{cx+b}$ có đồ thị như hình vẽ:
A. $a=2,b=2,c=-1$. B. $a=1,b=1,c=-1$. C. $a=1,b=2,c=1$. D. $a=1,b=-2,c=1$. |
Lời giải chi tiết
Dựa vào đồ thị hàm số đã cho ta thấy:
Đồ thị hàm số có tiệm cận đứng và tiệm cận ngang là $\left\{ \begin{array} {} x=2 \\ {} y=1 \\ \end{array} \right.\Rightarrow \left\{ \begin{array} {} -\frac{b}{a}=2 \\ {} \frac{a}{c}=1 \\ \end{array} \right.\Rightarrow \left\{ \begin{array} {} b=-2a \\ {} a=c \\ \end{array} \right.$
Đồ thị hàm số cắt các trục tọa độ tại các điểm $\left( 0;-1 \right),\,\,\left( -2;0 \right)\Rightarrow \left\{ \begin{array} {} \frac{2}{b}=-1 \\ {} -2a+2=0 \\ \end{array} \right.$
Suy ra $a=1,b=-2,c=1$. Chọn D.