20 Bài tập Tính chất của phép khai phương lớp 9 (sách mới) có đáp án

Bài tập Toán 9 Tính chất của phép khai phương

A. Bài tập Tính chất của phép khai phương

Bài 1. Tính:

Tính chất của phép khai phương (Lý thuyết Toán lớp 9) | Chân trời sáng tạo

Hướng dẫn giải

a) Ta có: $\sqrt{{(- 9)}^{2}} = |- 9| = 9.$

b) Ta có: $\sqrt{{(- \frac{6}{7})}^{2}} = |- \frac{6}{7}| = \frac{6}{7} .$

c) Ta có: ${(- \sqrt{3})}^{2} - \sqrt{36} = 3 - 6 = - 3.$

d) ${(\sqrt{\frac{4}{9}})}^{2} . \sqrt{0, 81} = \frac{4}{9} .0, 9 = \frac{4}{9} . \frac{9}{10} = \frac{2}{5} .$

Bài 2. Rút gọn các biểu thức sau:

a) $\sqrt{7^{2} .5};$

b) $\sqrt{100 a^{2}}$ với a < 0;

c) $\sqrt{6 b} . \sqrt{24 b} - 4 b$ với b ≥ 0.

Hướng dẫn giải

a) Ta có: $\sqrt{7^{2} .5} = 7 \sqrt{5} .$

b) Ta có: $\sqrt{100 a^{2}} = \sqrt{{(10 a)}^{2}} = |10 a| = - 10 a$ với a < 0.

c) Với b ≥ 0, ta có:

$\sqrt{6 b} . \sqrt{24 b} - 4 b = \sqrt{6 b .24 b} - 4 b = \sqrt{144 b^{2}} - 4 b$

$= \sqrt{{(12 b)}^{2}} - 4 b = |12 b| - 4 b = 12 b - 4 b = 8 b$

Bài 3. Cho hình chữ nhật có chiều rộng a (cm), chiều dài b (cm) và diện tích S (cm²).

a) Tìm S, biết $a = \sqrt{6},$ $b = \sqrt{48};$

b) Tìm a, biết $S = 5 \sqrt{6},$ $b = \sqrt{3} .$

Hướng dẫn giải

a) Ta có: S = a.b

$= \sqrt{6} . \sqrt{48}$ $= \sqrt{6.48}$

= $\sqrt{288}$ $= 12 \sqrt{2}$

Vậy $S = 12 \sqrt{2}$ cm².

b) Ta có: a = S : b

$= 5 \sqrt{6} : \sqrt{3}$

$= 5 \sqrt{\frac{6}{3}}$ $= 5 \sqrt{2}$

Vậy $a = 5 \sqrt{2}$ cm

B. Lý thuyết Tính chất của phép khai phương

1. Căn thức bậc hai của một bình phương

Tính chất

Với biểu thức A bất kì, ta có $\sqrt{A^{2}} = | A |$ , nghĩa là

$\sqrt{A^{2}} = A$ khi $A \geq 0$ ;

$\sqrt{A^{2}} = - A$ khi $A < 0$ .

Ví dụ: Với $x < 0$ , ta có 1 – x > 0. Do đó ${(\sqrt{1 - x})}^{2} = 1 - x$ .

2. Căn thức bậc hai của một tích

Với hai biểu thức A và B nhận giá trị không âm, ta có

$\sqrt{A} . \sqrt{B} = \sqrt{A B}$ .

Ví dụ:

$\sqrt{27} . \sqrt{3} = \sqrt{27.3} = \sqrt{81} = 9$

Với $a \geq 0, b < 0$ thì $\sqrt{25 a^{2} b^{2}} = \sqrt{5^{2} . a^{2} . {(- b)}^{2}} = \sqrt{5^{2}} . \sqrt{a^{2}} . \sqrt{{(- b)}^{2}} = 5. a . (- b) = - 5 a b$ .

Nhận xét: Ta có thể biến đổi $\sqrt{a b} = \sqrt{a} . \sqrt{b}$ hoặc $\sqrt{a} . \sqrt{b} = \sqrt{a b}$ ( $a \geq 0$ và $b \geq 0$ ) để việc tính toán được dễ dàng hơn.

Với số thực a bất kì và b không âm, ta có

$\sqrt{a^{2} b} = | a | \sqrt{b}$ .

Biến đổi này được gọi là đưa thừa số ra ngoài dấu căn.

Ngược lại, ta có biến đổi đưa thừa số vào trong dấu căn.

+ Nếu $a \geq 0$ thì $a \sqrt{b} = \sqrt{a^{2} b}$ .

+ Nếu $a < 0$ thì $a \sqrt{b} = - \sqrt{a^{2} b}$ .

Tổng quát, với hai biểu thức A và B mà $B \geq 0$ , ta có $\sqrt{A^{2} B} = | A | \sqrt{B}$ .

Ví dụ:

$\sqrt{75} = \sqrt{25.3} = \sqrt{5^{2} .3} = 5 \sqrt{3}$

$\sqrt{15 a} . \sqrt{3 a} = \sqrt{15 a .3 a} = \sqrt{3^{2} a^{2} .5} = | 3 a | \sqrt{5}$ .

2. Căn thức bậc hai của một thương

Tính chất

Với biểu thức A nhận giá trị không âm và biểu thức B nhận giá trị dương, ta có

$\sqrt{\frac{A}{B}} = \frac{\sqrt{A}}{\sqrt{B}}$ .

Ví dụ: $\sqrt{\frac{49}{64}} = \frac{\sqrt{49}}{\sqrt{64}} = \frac{7}{8}$ ;

$\sqrt{\frac{4 a^{2}}{25}} = \frac{\sqrt{4 a^{2}}}{\sqrt{25}} = \frac{\sqrt{4} . \sqrt{a^{2}}}{\sqrt{25}} = \frac{2 | a |}{5}$ ;

$\frac{\sqrt{8}}{\sqrt{2}} = \sqrt{\frac{8}{2}} = \sqrt{4} = 2$ ;

Với $a > 0$ thì $\frac{\sqrt{52 a^{3}}}{\sqrt{13 a}} = \sqrt{\frac{52 a^{3}}{13 a}} = \sqrt{4 a^{2}} = \sqrt{{(2 a)}^{2}} = 2 a$ .

Nhận xét: Ta có thể biến đổi $\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$ hoặc $\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}$ ( $a \geq 0$ và $b \geq 0$ ) để việc tính toán được dễ dàng hơn.

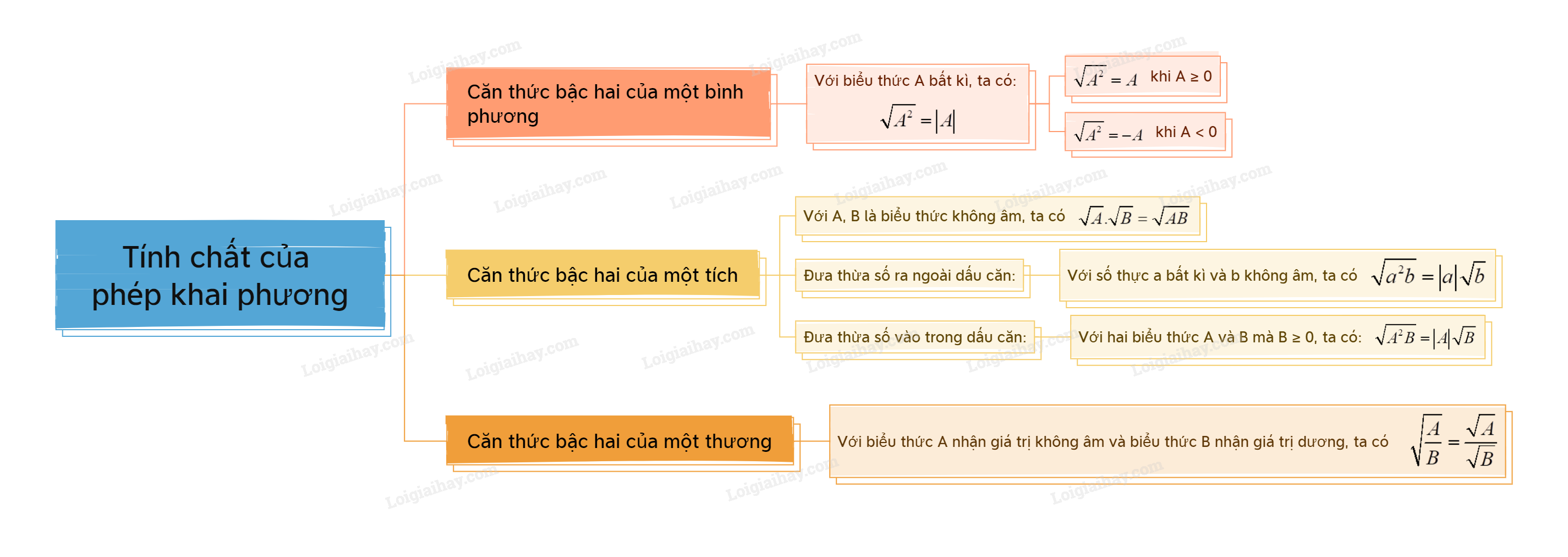
Sơ đồ tư duy Tính chất của phép khai phương

Bài liên quan