20 Bài tập Biến đổi đơn giản và rút gọn biểu thức chứa căn thức bậc hai lớp 9 (sách mới) có đáp án

Bài tập Toán 9 Biến đổi đơn giản và rút gọn biểu thức chứa căn thức bậc hai

A. Bài tập Biến đổi đơn giản và rút gọn biểu thức chứa căn thức bậc hai

Bài 1. Khử mẫu của biểu thức lấy căn:

Hướng dẫn giải

a) Ta có: $\sqrt{\frac{8}{9}} = \frac{\sqrt{8}}{\sqrt{9}} = \frac{2 \sqrt{2}}{3} .$

b) Ta có: $\sqrt{\frac{3}{11}} = \frac{\sqrt{3}}{\sqrt{11}} = \frac{\sqrt{3} . \sqrt{11}}{11} = \frac{\sqrt{33}}{11} .$

c) Ta có: $\sqrt{\frac{1}{5 a^{3}}} = \frac{\sqrt{1}}{\sqrt{5 a^{3}}} = \frac{1}{\sqrt{5 a . a^{2}}} = \frac{1}{a \sqrt{5 a}} = \frac{\sqrt{5 a}}{5 a^{2}}$ với a > 0.

d) Ta có: $3 a b \sqrt{\frac{a^{2}}{3 b}} = 3 a b . \frac{\sqrt{a^{2}}}{\sqrt{3 b}} = 3 a b . \frac{|a|}{\sqrt{3 b}}$

Vì a < 0 nên $|a| = - a .$ Suy ra $3 a b . \frac{|a|}{\sqrt{3 b}} = 3 a b . \frac{- a}{\sqrt{3 b}} = - \frac{3 a^{2} b . \sqrt{3 b}}{3 b} = - a^{2} \sqrt{3 b} .$

Bài 2. Đưa thừa số vào trong dấu căn:

a) $7 \sqrt{2};$

b) $- 3 \sqrt{5};$

c) $3 \sqrt{\frac{13}{9}};$

d) $- 4 \sqrt{\frac{13}{4} .}$

Hướng dẫn giải

a) Ta có: $7 \sqrt{2} = \sqrt{7^{2} .2} = \sqrt{49.2} = \sqrt{98} .$

b) Ta có: $- 3 \sqrt{5} = - \sqrt{3^{2} .5} = - \sqrt{9.5} = - \sqrt{45} .$

c) Ta có: $3 \sqrt{\frac{13}{9}} = \sqrt{3^{2} . \frac{13}{9}} = \sqrt{9. \frac{13}{9}} = \sqrt{13} .$

d) Ta có: $- 4 \sqrt{\frac{13}{4}} = - \sqrt{4^{2} . \frac{13}{4}} = - \sqrt{13.4} = - \sqrt{52} .$

Bài 3. Trục căn thức ở mẫu:

a) $\frac{7 + 2 \sqrt{3}}{\sqrt{3}};$

b) $\frac{1}{\sqrt{6} - 3};$

c) $\frac{5 + \sqrt{5}}{1 - \sqrt{5}};$

d) $\frac{\sqrt{8}}{\sqrt{2} + \sqrt{3}} .$

Hướng dẫn giải

a) Nhân cả tử và mẫu của biểu thức đã cho với $\sqrt{3},$ ta được:

$\frac{7 + 2 \sqrt{3}}{\sqrt{3}} = \frac{7 \sqrt{3} + 2.3}{3} = \frac{7 \sqrt{3} + 6}{3} .$

b) Biểu thức liên hợp của mẫu là $\sqrt{6} + 3.$ Nhân cả tử và mẫu của biểu thức đã cho với $\sqrt{6} + 3,$ ta được:

$\frac{1}{\sqrt{6} - 3} = \frac{\sqrt{6} + 3}{(\sqrt{6} - 3) (\sqrt{6} + 3)} = \frac{\sqrt{6} + 3}{6 - 9} = - \frac{\sqrt{6} + 3}{3} .$

c) Biểu thức liên hợp của mẫu là $1 + \sqrt{5} .$ Nhân cả tử và mẫu của biểu thức đã cho với $1 + \sqrt{5},$ ta được:

$\frac{5 + \sqrt{5}}{1 - \sqrt{5}} = \frac{\sqrt{5} {(1 + \sqrt{5})}^{2}}{(1 - \sqrt{5}) (1 + \sqrt{5})} = \frac{\sqrt{5} (6 + 2 \sqrt{5})}{1 - 5} = - \frac{6 \sqrt{5} + 10}{4} = - \frac{3 \sqrt{5} + 5}{2} .$

d) Biểu thức liên hợp của mẫu là $\sqrt{2} - \sqrt{3} .$ Nhân cả tử và mẫu của biểu thức đã cho với $\sqrt{2} - \sqrt{3},$ ta được:

$\frac{\sqrt{8}}{\sqrt{2} + \sqrt{3}} = \frac{\sqrt{8} (\sqrt{2} - \sqrt{3})}{(\sqrt{2} + \sqrt{3}) (\sqrt{2} - \sqrt{3})} = \frac{\sqrt{16} - \sqrt{24}}{2 - 3} = 2 \sqrt{6} - 4.$

Bài 4. Trục căn thức ở mẫu các biểu thức sau:

Hướng dẫn giải

a) Ta có:

b) Ta có:

c) Ta có:

Bài 5. Tính:

Hướng dẫn giải

a) Ta có:

b) Ta có:

c) Ta có:

B. Lý thuyết Biến đổi đơn giản và rút gọn biểu thức chứa căn thức bậc hai

1. Đưa thừa số ra ngoài dấu căn

Phép đưa thừa số ra ngoài dấu căn

Nếu a là một số và b là một số không âm thì $\sqrt{a^{2} . b} = | a | \sqrt{b}$ .

Ví dụ:

$\sqrt{45} = \sqrt{3^{2} .5} = 3 \sqrt{5}$ ;

$\sqrt{243 a} = \sqrt{9^{2} .3 a} = 9 \sqrt{3 a}$ .

Với những căn thức bậc hai mà biểu thức dưới dấu căn có mẫu, ta thường khử mẫu của biểu thức lấy căn (biến đổi căn thức bậc hai đó thành một biểu thức mà trong căn thức không còn mẫu).

Ví dụ: $\sqrt{\frac{4}{7}} = \sqrt{\frac{4.7}{7^{2}}} = \sqrt{{(\frac{2}{7})}^{2} .7} = \frac{2 \sqrt{7}}{7}$ .

2. Đưa thừa số vào trong dấu căn

Phép đưa thừa số vào trong dấu căn

– Nếu a và b là hai số không âm thì $a \sqrt{b} = \sqrt{a^{2} b}$ .

– Nếu a là số âm và b là số không âm thì $a \sqrt{b} = - \sqrt{a^{2} b}$ .

Ví dụ:

$5 \sqrt{2} = \sqrt{5^{2} .2} = \sqrt{50}$ ;

Với $a \geq 0$ thì $- 2 \sqrt{a} = - \sqrt{2^{2} . a} = - \sqrt{4 a}$ .

3. Trục căn thức ở mẫu

Cách trục căn thức ở mẫu

– Với các biểu thức A, B và B > 0, ta có $\frac{A}{\sqrt{B}} = \frac{A \sqrt{B}}{B}$ .

– Với các biểu thức A, B, C mà $A \geq 0, A \neq B^{2}$ , ta có:

$\frac{C}{\sqrt{A} + B} = \frac{C (\sqrt{A} - B)}{A - B^{2}}; \frac{C}{\sqrt{A} - B} = \frac{C (\sqrt{A} + B)}{A - B^{2}}$ .

– Với các biểu thức A, B, C mà $A \geq 0, B \geq 0, A \neq B$ , ta có:

$\frac{C}{\sqrt{A} + \sqrt{B}} = \frac{C (\sqrt{A} - \sqrt{B})}{A - B}; \frac{C}{\sqrt{A} - \sqrt{B}} = \frac{C (\sqrt{A} + \sqrt{B})}{A - B}$ .

Ví dụ:

$\frac{2}{3 \sqrt{5}} = \frac{2 \sqrt{5}}{3 {(\sqrt{5})}^{2}} = \frac{2 \sqrt{5}}{3.5} = \frac{2 \sqrt{5}}{15}$ ;

$\frac{a}{3 - 2 \sqrt{2}} = \frac{a (3 + 2 \sqrt{2})}{(3 - 2 \sqrt{2}) . (3 + 2 \sqrt{2})} = \frac{a (3 + 2 \sqrt{2})}{3^{2} - {(2 \sqrt{2})}^{2}} = \frac{a (3 + 2 \sqrt{2})}{9 - 8} = (3 + 2 \sqrt{2}) a$ .

4. Rút gọn biểu thức chứa căn thức bậc hai

Khi rút gọn biểu thức có chứa căn thức bậc hai, ta cần phối hợp các phép tính (cộng, trừ, nhân, chia) và các phép biến đổi đã học (đưa thừa số ra ngoài hoặc vào trong dấu căn; khử mẩu của biểu thức lấy căn; trục căn thức ở mẫu).

Ví dụ:

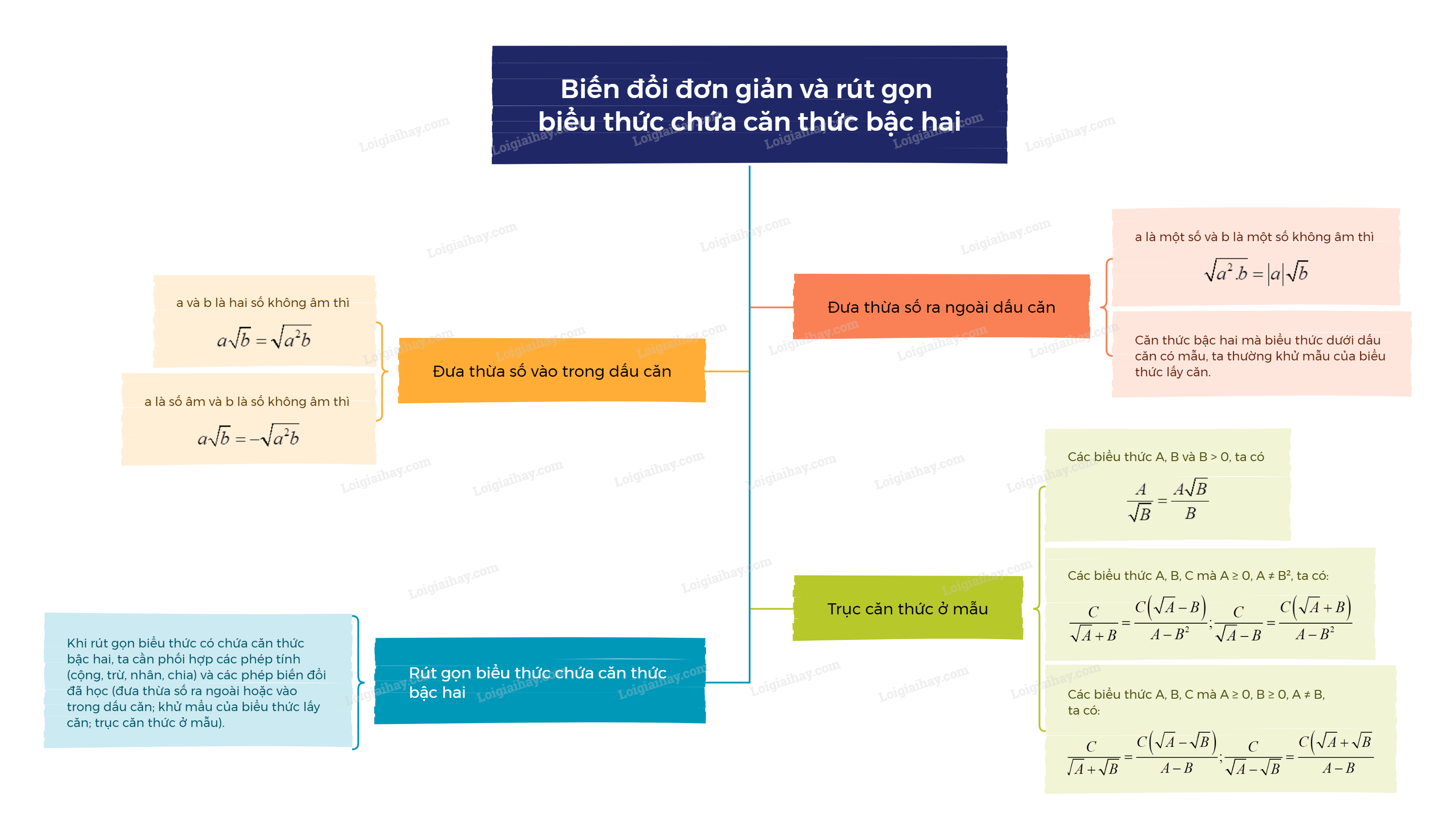
$\begin{array}{l} A = 2 \sqrt{3} - \sqrt{75} + \sqrt{{(1 - \sqrt{3})}^{2}} \\ = 2 \sqrt{3} - \sqrt{{3.5}^{2}} + | 1 - \sqrt{3} | \\ = 2 \sqrt{3} - 5 \sqrt{3} + \sqrt{3} - 1 \\ = - 1 - 2 \sqrt{3} \end{array}$

$\begin{array}{l} B = x \sqrt{x} - \frac{x^{2} - x}{\sqrt{x} + 1} \\ = x \sqrt{x} - \frac{(x^{2} - x) (\sqrt{x} - 1)}{(\sqrt{x} + 1) (\sqrt{x} - 1)} \\ = x \sqrt{x} - \frac{x (x - 1) (\sqrt{x} - 1)}{(\sqrt{x} + 1) (\sqrt{x} - 1)} \\ = x \sqrt{x} - \frac{x (x - 1) (\sqrt{x} - 1)}{x - 1} \\ = x \sqrt{x} - x (\sqrt{x} - 1) \\ = x \sqrt{x} - x \sqrt{x} + x \\ = x \end{array}$

Sơ đồ tư duy Biến đổi đơn giản và rút gọn biểu thức chứa căn thức bậc hai

Bài liên quan:

Để lại một bình luận Huỷ trả lời