Bài tập Toán 9 Khai căn bậc hai với phép nhân và phép chia
A. Bài tập Khai căn bậc hai với phép nhân và phép chia
Bài 1. Cho căn thức
a) Hãy chứng tỏ rằng căn thức xác định với mọi giá trị của x;
b) Rút gọn căn thức đã cho với x ≥ 1;
c) Chứng tỏ rằng với mọi x ≥ 1, biểu thức có giá trị không đổi.
Hướng dẫn giải
a) Điều kiện xác định của căn thức là x2 – 2x + 1 ≥ 0 ⇔ (x2 – 1) ≥ 0 ∀ x
Suy ra căn thức xác định với mọi giá trị của x.
b) Với x ≥ 1, ta có:
c) Với x ≥ 1, ta có:
Bài 2. Chứng minh rằng:
a)
b)
Hướng dẫn giải
a) Ta có: VT =
(ĐPCM).
b) Ta có:
(ĐPCM).
Bài 3. Rút gọn các biểu thức sau:
a)
b)
c)
d) với x ≥ 0; x ≠ 4.
Hướng dẫn giải
a) Ta có:
.
b) Ta có:
c) Ta có:
d) Ta có: (x ≥ 0; x ≠ 4)
Bài 4. Điện áp V (tính theo volt) yêu cầu cho một mạch điện được cho bởi công thức trong đó P là công suất (tính theo watt) và R là điện trở trong (tính theo ohm).
a) Cần bao nhiêu volt để thắp sáng một bóng đèn A có công suất 100 watt và điện trở của mỗi bóng đèn là 110 ohm?;
b) Bóng đèn B có điện áp bằng 110 volt, điện trở trong là 88 ohm có công suất lớn hơn bóng đèn A không? Giải thích.
Hướng dẫn giải
a) Thay P = 100, R = 110 vào công thức ta được:
(volt)
Vậy số volt để thắp sáng một bóng đèn A là 104,88 (volt).
b) Thay V = 110, R = 88 vào công thức ta được:
⇒ P.88 = (110)2 ⇒ (watt) > 100 (watt)
Vậy bóng đèn B có công suất lớn hơn bóng đèn A.
B. Lý thuyết Khai căn bậc hai với phép nhân và phép chia
1. Khai căn bậc hai và phép nhân
Liên hệ giữa phép khai căn bậc hai và phép nhân
Với A, B là biểu thức không âm, ta có . |
Ví dụ:
Chú ý:
– Kết quả trên có thể mở rộng cho nhiều biểu thức không âm, chẳng hạn:
(với ).
Ví dụ:
– Nếu thì .
Ví dụ: Với thì
2. Khai căn bậc hai và phép chia
Liên hệ giữa phép khai căn bậc hai và phép chia
Nếu A, B là các biểu thức với thì . |
Ví dụ: ;
Với thì .
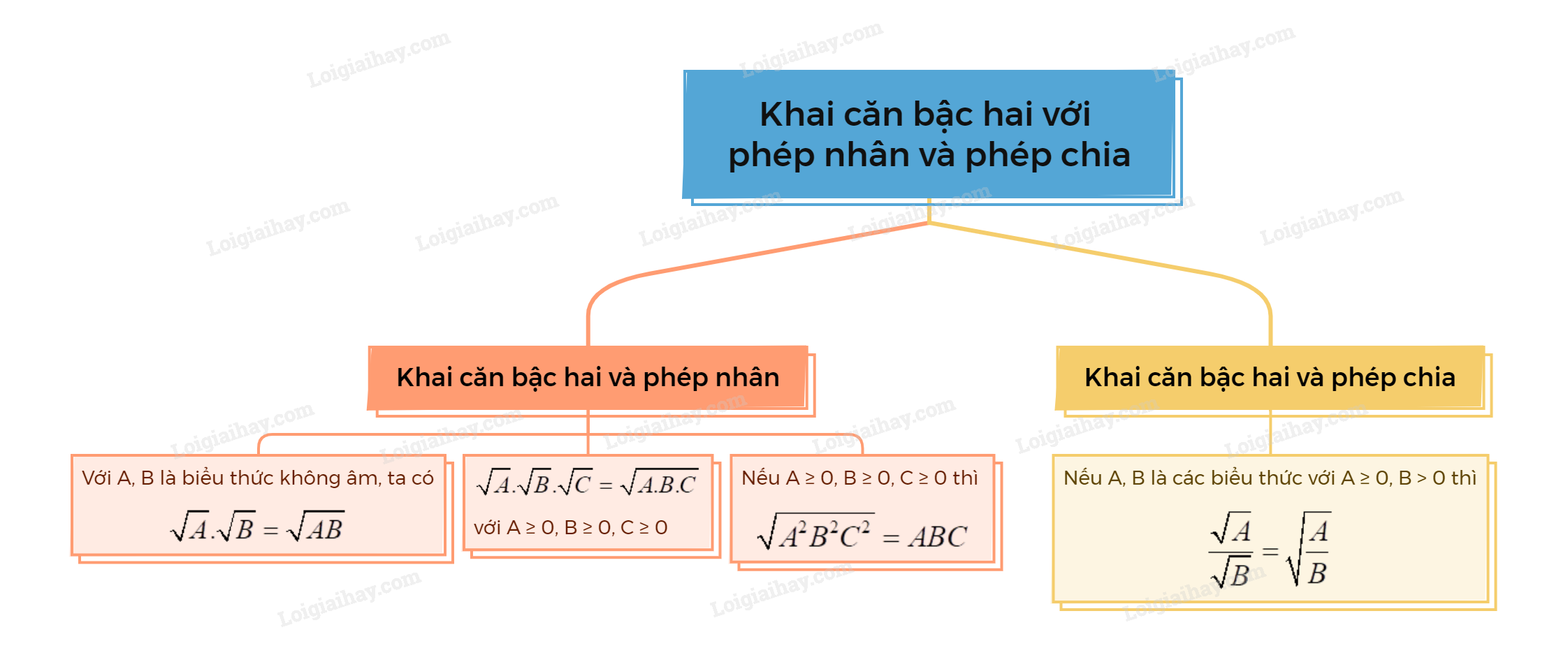
Sơ đồ tư duy Khai căn bậc hai với phép nhân và phép chia