PHƯƠNG PHÁP GIẢI NHANH CÁC DẠNG BÀI TẬP VỀ GEN & ADN
Bài 1: Một phân tử ADN có tổng số 60000 nuclêôtit. Hãy xác định chiều dài và số chu kì xoắn của ADN này.
Lời giải chi tiết
Công thức giải nhanh:
| Một phân tử ADN có tổng số nuclêôtit là N thì số chu kì xoắn $=\frac{N}{20}$; Chiều dài của ADN $=\frac{N}{2}\times 3,4$ (tính theo đơn vị Å). |
Giải thích lí thuyết:
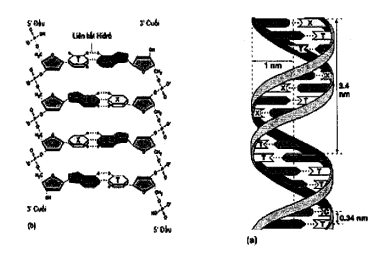
– ADN có cấu trúc xoắn kép, trong đó mỗi chu kì xoắn có chiều dài 34Å và có 10 cặp nuclêôtit. Do đó, cứ 1 cặp nuclêôtit thì tương đương độ dài 3,4Å.
– Vì vậy, một phân tử ADN có N nuclêôtit thì sẽ có chiều dài $L=\frac{N}{2}\times 3,4$.
– Một phân tử ADN có N nuclêôtit thì sẽ có số chu kì xoắn $=\frac{N}{20}$.
Áp dụng công thức giải nhanh vào bài toán, ta có:
– Chiều dài của ADN này $=\frac{N}{2}\times 3,4=\frac{60000}{2}\times 3,4=102000$ (Å).
– Số chu kì xoắn của ADN $=\frac{N}{20}=\frac{60000}{20}=3000$ (chu kì xoắn).
Bài tập vận dụng:
Bài tập 1: Một phân tử ADN có chiều dài 9160 nm. Hãy xác định tổng số nuclêôtit của ADN và số chu kì xoắn của ADN này.
Lời giải chi tiết
Áp dụng công thức giải nhanh, ta có:
– Chiều dài của ADN, $L=\frac{N}{2}\times 3,4\to N=\frac{L\times 2}{3,4}$
– ADN có chiều dài 9160 nm = 91600Å.
$\to $ Tổng số nuclêôtit của ADN là $=\frac{91600}{3,4}\times 2=48000$ (nu).
– Số chu kì xoắn của ADN $=\frac{N}{20}=\frac{48000}{20}=2400$ (chu kì xoắn).
Bài tập 2: Một gen có 220 chu kì xoắn. Hãy xác định tổng số nuclêôtit và chiều dài của gen này.
Lời giải chi tiết
Gen là một đoạn ADN cho nên áp dụng công thức giải“` ` ` nhanh của ADN, ta có:
– Chiều dài của ADN, L $=$ số chu kì xoắn $\times 34=220\times 34=7480$ (Å).
– Tổng số nuclêôtit của ADN là $=$ số chu kì xoắn $\times 20=220\times 20=4400$ (chu kì).
Bài 2: Một phân tử ADN có tổng số 480000 nuclêôtit và số nuclêôtit loại G chiếm 22% tổng số nuclêôtit của ADN. Hãy xác định số nuclêôtit mỗi loại và tổng liên kết hiđrô của ADN này.
Lời giải chi tiết
Công thức giải nhanh
| Tổng số 2 loại nuclêôtit không bổ sung luôn chiếm 50% tổng số nuclêôtit của ADN. A + G = A + X = T + G = T + X = 50%.
Tổng số liên kết hiđrô của phân tử ADN là = 2A + 3G = Tổng số nuclêôtit của ADN + Gcủa ADN. |
Giải thích lí thuyết:
| – Vì $A+T+G+X=100%$.
Mà $A=T$ và $G=X$ cho nên $A+T=2A;\,\,G+X=2G$. $\to A+T+G+X=2A+2G=100%.\,\,\,\to A+G=50%$. – Trên phân tử ADN mạch kép, A liên kết với T bằng 2 liên kết hiđrô; G liên kết với X bằng 3 liên kết hiđrô. Do đó, ở đâu có A và T thì ở đó có 2 liên kết hiđrô, ở đâu có G và X thì ở đó có 3 liên kết hiđrô. $\to $ Số liên kết hiđrô $=2A+3G$. – $H=2A+3G=2A+2G+G$. Vì $2A+2G=N$. $\to H=N+G$. Áp dụng công thức giải nhanh, ta có: $\,\,\,\,\,\,\,G=22%\to A=50%-22%=28%$. – Số nuclêôtit loại $A=T=28%\times 480000=134400$ – Số nuclêôtit loại $G=X=22%\times 480000=105600$ – Số liên kết hiđrô của ADN là $\,\,\,\,\,H=2A+3G=N+G=480000+105600=585600$ (liên kết) |
Bài 3: Một phân tử ADN có tổng số 310000 nuclêôtit và 390000 liên kết hiđrô. Hãy xác định số nuclêôtit mỗi loại của ADN này.
Lời giải chi tiết
Công thức giải nhanh:
| Một phân tử ADN có tổng số nuclêôtit là N; tổng liên kết hiđrô là H thì số nuclêôtit loại G = H – N; số nu loại A = 1,5N – H. |
Giải thích:
a) Chứng minh G luôn $=H-N$.
Tổng số nuclêôtit của ADN là $N=2A+2G$.
Tổng liên kết hiđrô của ADN là $H=2A+3G$.
Vì vậy, nếu lấy $H-N$ thì ta có: $H-N=2A+3G-\left( 2A+2G \right)=G$.
$\to $ Số nuclêôtit loại G luôn $=H-N$.
b) Chứng minh A luôn $=1,5N-H$.
$N=2A+2G.\to 1,5N=3A+3G$.
Do đó, $1,5N-H=3A+3G-\left( 2A+3G \right)=A$.
$\to $ Số nuclêôtit loại A luôn $=1,5N-H$.
Áp dụng công thức giải nhanh, ta có:
$\,\,\,\,\,N=310000;\,\,H=390000$.
$\to A=T=H-N=390000-310000=80000$.
$\to G=X=1,5N-H=1,5\times 310000-390000=465000-390000=75000$.
Bài tập vận dụng:
Một gen có tổng số 5100 nuclêôtit và 6050 liên kết hiđrô. Hãy xác định số nuclêôtit mỗi loại của gen này.
Lời giải chi tiết
Áp dụng công thức giải nhanh, ta có:
$\,\,\,\,\,\,\,N=5100;\,\,H=6050$.
$\to A=T=H-N=6050-5100=950$.
$\to G=X=1,5N-H=1,5\times 5100-6050=7650-5100=2550$.
Bài 4: Trên mạch một của một phân tử ADN có tỉ lệ $\frac{A+G}{T+X}=\frac{1}{4}$. Tỉ lệ này ở mạch thứ hai là bao nhiêu?
Lời giải chi tiết
Công thức giải nhanh:
| Ở phân tử ADN mạch kép, nếu tỉ lệ hai loại nuclêôtit không bổ sung ở mạch thứ nhất $=\frac{a}{b}$ thì tỉ lệ của hai loại nuclêôtit này ở mạch thứ 2 $=\frac{b}{a}$.
Minh họa công thức: – Nếu $\frac{{{A}_{1}}+{{G}_{1}}}{{{T}_{1}}+{{X}_{1}}}=\frac{a}{b}$ thì tỉ lệ $\frac{{{A}_{2}}+{{G}_{2}}}{{{T}_{2}}+{{X}_{2}}}=\frac{b}{a}$. – Nếu $\frac{{{A}_{1}}+{{X}_{1}}}{{{T}_{1}}+{{G}_{1}}}=\frac{a}{b}$ thì tỉ lệ $\frac{{{A}_{2}}+{{X}_{2}}}{{{T}_{2}}+{{G}_{2}}}=\frac{b}{a}$. – Nếu $\frac{{{T}_{1}}+{{X}_{1}}}{{{A}_{1}}+{{G}_{1}}}=\frac{a}{b}$ thì tỉ lệ $\frac{{{T}_{2}}+{{X}_{2}}}{{{A}_{2}}+{{G}_{2}}}=\frac{b}{a}$. |
Giải thích:
$\frac{{{A}_{1}}+{{G}_{1}}}{{{T}_{1}}+{{X}_{1}}}=\frac{a}{b}$ thì $\frac{{{A}_{2}}+{{G}_{2}}}{{{T}_{2}}+{{X}_{2}}}=\frac{b}{a}$.
– Vì hai mạch của ADN liên kết bổ sung với nhau cho nên A của mạch này $=T$ của mạch kia; G của mạch này $=X$ của mạch kia.
Do đó, ${{A}_{2}}+{{G}_{2}}={{T}_{1}}+{{X}_{1}};\,\,{{T}_{2}}+{{X}_{2}}={{A}_{1}}+{{G}_{1}}$.
– Ta có $\frac{{{A}_{2}}+{{G}_{2}}}{{{T}_{2}}+{{X}_{2}}}=\frac{{{T}_{1}}+{{X}_{1}}}{{{A}_{1}}+{{G}_{1}}}=\frac{\frac{1}{{{A}_{1}}+{{G}_{1}}}}{{{T}_{1}}+{{X}_{1}}}=\frac{\frac{1}{a}}{b}=\frac{b}{a}$.
Áp dụng công thức giải nhanh, ta có tỉ lệ $\frac{A+G}{T+X}$ ở mạch 2 $=\frac{4}{1}$.
Bài tập vận dụng:
Trên mạch một của một gen có tỉ lệ $\frac{A+X}{T+G}=0,3$. Tỉ lệ này ở mạch thứ hai là bao nhiêu?
Lời giải chi tiết
Gen là một đoạn ADN, cho nên áp dụng công thức giải nhanh của ADN, ta có:
Mạch 1 có tỉ lệ $\frac{A+X}{T+G}=0,3=\frac{3}{10}$ thì ở mạch 2, tỉ lệ $\frac{A+X}{T+G}=\frac{10}{3}$.
Bài 5: Một phân tử ADN có tổng số 24000 nuclêôtit và trên mạch 2 của ADN này có tỉ lệ $A:T:G:X=4:6:5:9$. Hãy xác định số nuclêôtit mỗi loại ở mạch 2 của ADN này.
Lời giải chi tiết
Công thức giải nhanh:
| Một phân tử ADN mạch kép có tổng số nuclêôtit là N và trên mạch 1 của ADN có tỉ lệ các loại nuclêôtit A : T : G : X = a : t : g : x, thì số nuclêôtit mỗi loại của mạch 1 là:
${{A}_{1}}=\frac{a\times N}{2\left( a+t+g+x \right)}$; $\,{{T}_{1}}=\frac{t\times N}{2\left( a+t+g+x \right)}$; ${{G}_{1}}=\frac{g\times N}{2\left( a+t+g+x \right)}$; ${{X}_{1}}=\frac{x\times N}{2\left( a+t+g+x \right)}$. |
Chứng minh công thức:
– Tổng số nuclêôtit của mạch 1 $=\frac{N}{2}$.
– Tỉ lệ ${{A}_{1}}:{{T}_{1}}:{{G}_{1}}:{{X}_{1}}=a:t:g:x$.
$\to \frac{{{A}_{1}}}{a}=\frac{{{T}_{1}}}{t}=\frac{{{G}_{1}}}{g}=\frac{{{X}_{1}}}{x}=\frac{{{A}_{1}}+{{T}_{1}}+{{G}_{1}}+{{X}_{1}}}{a+t+g+x}=\frac{\frac{N}{2}}{a+t+g+x}=\frac{N}{2\left( a+t+g+x \right)}$
$\to {{A}_{1}}=\frac{a\times N}{2\left( a+t+g+x \right)}$; ${{T}_{1}}=\frac{t\times N}{2\left( a+t+g+x \right)}$;
${{G}_{1}}=\frac{g\times N}{2\left( a+t+g+x \right)}$; ${{X}_{1}}=\frac{x\times N}{2\left( a+t+g+x \right)}$
Vận dụng công thức giải nhanh, ta có:
${{A}_{1}}=\frac{4\times 24000}{2\left( 4+6+5+9 \right)}=\frac{96000}{48}=2000$;
${{T}_{1}}=\frac{6\times 24000}{2\left( 4+6+5+9 \right)}=\frac{144000}{48}=3000$;
${{G}_{1}}=\frac{5\times 24000}{2\left( 4+6+5+9 \right)}=\frac{120000}{48}=2500$;
${{X}_{1}}=\frac{9\times 24000}{2\left( 4+6+5+9 \right)}=\frac{216000}{48}=4500$
Bài tập vận dụng:
Bài tập 1: Một gen có tổng số 2400 nuclêôtit và trên mạch 2 của gen này có tỉ lệ $A:T:G:X=1:3:4:4$. Hãy xác định số nuclêôtit mỗi loại ở mạch 2 của gen này.
Cách tính:
Vận dụng công thức giải nhanh, ta có:
${{A}_{2}}=\frac{1\times 2400}{2\left( 1+3+4+4 \right)}=\frac{2400}{24}=100$;
${{T}_{2}}=\frac{3\times 2400}{2\left( 1+3+4+4 \right)}=\frac{7200}{24}=300$;
${{G}_{2}}=\frac{4\times 2400}{2\left( 1+3+4+4 \right)}=\frac{9600}{24}=400$;
${{X}_{2}}=\frac{4\times 2400}{2\left( 1+3+4+4 \right)}=\frac{9600}{24}=400$.
Bài tập 2: Một gen có chiều dài 510nm và trên mạch 1 của gen này có tỉ lệ $A:T:G:X=3:5:4:3$. Hãy xác định số nuclêôtit mỗi loại ở mạch 1 của gen này.
Cách tính:
– Gen có chiều dài 510nm $\to $ Tổng số nuclêôtit của gen $=\frac{5100}{3,4}\times 2=3000$.
Vận dụng công thức giải nhanh, ta có:
${{A}_{1}}=\frac{3\times 3000}{2\left( 3+5+4+3 \right)}=\frac{9000}{30}=300$;
${{T}_{1}}=\frac{5\times 3000}{2\left( 3+5+4+3 \right)}=\frac{15000}{30}=500$;
${{G}_{1}}=\frac{4\times 3000}{2\left( 3+5+4+3 \right)}=\frac{12000}{30}=400$;
${{X}_{1}}=\frac{3\times 3000}{2\left( 3+5+4+3 \right)}=\frac{9000}{30}=300$
Bài 6: Một đoạn phân tử ADN có tổng số 1200 nuclêôtit và trên mạch 1 của đoạn ADN này có tỉ lệ $A:T:G:X=2:3:1:4$.
a. Hãy xác định số nuclêôtit mỗi loại trên mạch 1 của đoạn ADN.
b. Hãy xác định số nuclêôtit mỗi loại của đoạn ADN.
Lời giải chi tiết
Công thức giải nhanh:
| Hai mạch của phân tử ADN có chiều ngược nhau và liên kết theo nguyên tắc bổ sung, cho nên AADN = TADN = A1 + T1; GADN = XADN = G1 + X1. |
Giải thích:
– ADN có 2 mạch cho nên số nuclêôtit loại A của cả ADN bằng tổng số nuclêôtit loại A trên mạch 1 với loại A trên mạch 2 $={{A}_{1}}+{{A}_{2}}$.
– Vì 2 mạch của ADN liên kết bổ sung cho nên số nuclêôtit loại A của mạch 2 bằng số nuclêôtit loại T của mạch 1 $\left( {{A}_{2}}={{T}_{1}} \right)$.
$\to {{A}_{ADN}}={{A}_{1}}+{{A}_{2}}={{A}_{1}}+{{T}_{1}}$.
Suy luận tương tự như trên, ta có ${{G}_{ADN}}={{G}_{1}}+{{G}_{2}}={{G}_{1}}+{{X}_{1}}$.
a. Xác định số nuclêôtit mỗi loại trên mạch 1 của đoạn ADN
Vận dụng công thức giải nhanh, ta có số nuclêôtit mỗi loại trên mạch 1 của đoạn ADN này:
${{A}_{1}}=\frac{2\times 1200}{2\left( 2+3+1+4 \right)}=\frac{2400}{20}=120$.; ${{T}_{1}}=\frac{3\times 1200}{2\left( 2+3+1+4 \right)}=\frac{3600}{20}=180$;
${{G}_{1}}=\frac{1\times 1200}{2\left( 2+3+1+4 \right)}=\frac{1200}{20}=60$; ${{X}_{1}}=\frac{4\times 1200}{2\left( 2+3+1+4 \right)}=\frac{4800}{20}=240$.
b. Xác định số nuclêôtit mỗi loại của đoạn ADN
Vận dụng công thức giải nhanh, ta có:
${{A}_{ADN}}={{T}_{ADN}}={{A}_{1}}+{{T}_{1}}=120+180=300$
${{G}_{ADN}}={{X}_{ADN}}={{G}_{1}}+{{X}_{1}}=60+240=300$
Bài tập vận dụng: Một gen có tổng số 120 chu kì xoắn và trên mạch 2 của đoạn gen này có tỉ lệ $A:T:G:X=2:3:1:4$. Hãy xác định số nuclêôtit mỗi loại của gen.
Cách tính:
– Gen có 120 chu kì xoắn.
$\to $ Tổng số nuclêôtit của gen $=120\times 20=2400$.
– Muốn xác định số nuclêôtit mỗi loại của gen thì phải tính số nuclêôtit mỗi loại trên mạch 1. Vận dụng công thức giải nhanh, ta có số nuclêôtit mỗi loại trên mạch 1 của gen này:
${{A}_{1}}=\frac{2\times 2400}{2\left( 2+3+1+4 \right)}=\frac{4800}{20}=240$; ${{T}_{1}}=\frac{3\times 2400}{2\left( 2+3+1+4 \right)}=\frac{7200}{20}=360$;
${{G}_{1}}=\frac{1\times 2400}{2\left( 2+3+1+4 \right)}=\frac{2400}{20}=120$; ${{X}_{1}}=\frac{4\times 2400}{2\left( 2+3+1+4 \right)}=\frac{9600}{20}=480$.
– Xác định số nuclêôtit mỗi loại của gen
Vận dụng công thức giải nhanh, ta có:
${{A}_{ADN}}={{T}_{ADN}}={{A}_{1}}+{{T}_{1}}=240+360=600$
${{G}_{ADN}}={{X}_{ADN}}={{G}_{1}}+{{X}_{1}}=120+480=600$
Bài 7: Một gen có tổng số 3900 liên kết hiđrô và trên mạch 2 của đoạn gen này có tỉ lệ $A:T:G:X=1:3:2:4$. Hãy xác định số nuclêôtit mỗi loại của gen.
Lời giải chi tiết
Công thức giải nhanh:
| Một phân tử ADN có tổng số liên kết hiđrô là H; có tỉ lệ các loại nuclêôtit trên mạch 1 là A:T:G:X=a:t:g:x thì:
– Số nuclêôtit mỗi loại của mạch 1 là: ${{A}_{1}}=\frac{a.H}{2\left( a+t \right)+3\left( g+x \right)};\,\,{{A}_{1}}=\frac{a.H}{2\left( a+t \right)+3\left( g+x \right)};$ ${{G}_{1}}=\frac{g.H}{2\left( a+t \right)+3\left( g+x \right)};\,\,{{X}_{1}}=\frac{x.H}{2\left( a+t \right)+3\left( g+x \right)}$. – Số nuclêôtit mỗi loại của ADN là: ${{A}_{ADN}}={{T}_{ADN}}=\frac{\left( a+t \right).H}{2\left( a+t \right)+3\left( g+x \right)};\,\,{{G}_{ADN}}={{X}_{ADN}}=\frac{\left( g+x \right).H}{2\left( a+t \right)+3\left( g+x \right)}$. |
Chứng minh công thức:
– Tỉ lệ ${{A}_{1}}:{{T}_{1}}:{{G}_{1}}:{{X}_{1}}=a:t:g:x.\to \frac{{{A}_{1}}}{a}=\frac{{{T}_{1}}}{t}=\frac{{{G}_{1}}}{g}=\frac{{{X}_{1}}}{x}$.
Đưa các đại lượng ${{T}_{1}},\,\,{{G}_{1}},\,{{X}_{1}}$ về ẩn ${{A}_{1}}$.
Ta có: ${{T}_{1}}=\frac{t.{{A}_{1}}}{a};\,\,{{G}_{1}}=\frac{g.{{A}_{1}}}{a};\,\,{{X}_{1}}=\frac{x.{{A}_{1}}}{a}$.
– Tổng liên kết hiđrô của ADN $=2A+3G$.
Mà ${{A}_{ADN}}={{A}_{1}}+{{T}_{1}}={{A}_{1}}+\frac{t.{{A}_{1}}}{a}=\frac{a.{{A}_{1}}+t.{{A}_{1}}}{a}=\frac{{{A}_{1}}}{a}\left( a+t \right)$
${{G}_{ADN}}={{G}_{1}}+{{X}_{1}}=\frac{g.{{A}_{1}}}{a}+\frac{x.{{A}_{1}}}{a}=\frac{g.{{A}_{1}}+x.{{A}_{1}}}{a}=\frac{{{A}_{1}}}{a}\left( g+x \right)$
$\to $ Tổng liên kết hiđrô của ADN
$H=2A+3G=2.\frac{{{A}_{1}}}{a}\left( a+t \right)+3.\frac{{{A}_{1}}}{a}\left( g+x \right)=\frac{{{A}_{1}}}{a}\left( 2a+2t+3g+3x \right)$.
– Số nuclêôtit mỗi loại trên mạch 1 của ADN là:
${{A}_{1}}=\frac{a.H}{\left( 2a+2t+3g+3x \right)};\,\,{{T}_{1}}=\frac{t.H}{\left( 2a+2t+3g+3x \right)};$
${{G}_{1}}=\frac{g.H}{\left( 2a+2t+3g+3x \right)};\,\,{{X}_{1}}=\frac{x.H}{\left( 2a+2t+3g+3x \right)}$.
– Số nuclêôtit mỗi loại của ADN là:
${{A}_{ADN}}={{T}_{ADN}}=\frac{a.H}{\left( 2a+2t+3g+3x \right)}+\frac{t.H}{\left( 2a+2t+3g+3x \right)}=\frac{\left( a+t \right).H}{\left( 2a+2t+3g+3x \right)};$
${{G}_{ADN}}={{X}_{ADN}}=\frac{g.H}{\left( 2a+2t+3g+3x \right)}+\frac{x.H}{\left( 2a+2t+3g+3x \right)}=\frac{\left( g+x \right).H}{\left( 2a+2t+3g+3x \right)}$.
Cách tính:
Ta có $H=3900;\,\,a=1;\,\,t=3;\,\,g=2;\,\,x=4$.
Áp dụng công thức giải nhanh, ta có số nuclêôtit mỗi loại của gen là:
${{A}_{ADN}}={{T}_{ADN}}=\frac{\left( a+t \right).H}{2\left( a+t \right)+3\left( g+x \right)}=\frac{\left( 1+3 \right)\times 3900}{2\times \left( 1+3 \right)+3\times \left( 2+4 \right)}=\frac{15600}{26}=600$.
${{G}_{ADN}}={{X}_{ADN}}=\frac{\left( g+x \right).H}{2\left( a+t \right)+3\left( g+x \right)}=\frac{\left( 2+4 \right)\times 3900}{2\times \left( 1+3 \right)+3\times \left( 2+4 \right)}=\frac{23400}{26}=900$.
Bài tập vận dụng: Môt đoạn phân tử ADN có tổng số 1288 liên kết hiđrô và trên mạch một của đoạn ADN này có số nuclêôtit loại $T=1,5A$; có $G=A+T$; có $X=T-A$. Hãy xác định:
a. Số nuclêôtit mỗi loại trên mạch 1 của đoạn ADN.
b. Số nuclêôtit mỗi loại của đoạn ADN.
Lời giải chi tiết
$H=1288$;
${{T}_{1}}=1,5{{A}_{1}};\,\,{{G}_{1}}={{A}_{1}}+{{T}_{1}};\,\,{{X}_{1}}={{T}_{1}}-{{A}_{1}}$
$\to {{G}_{1}}={{A}_{1}}+1,5{{A}_{1}}=2,5{{A}_{1}}.{{X}_{1}}=1,5{{A}_{1}}-{{A}_{1}}=0,5{{A}_{1}}$.
$\to $ Tỉ lệ các loại nuclêôtit trên mạch 1 là
$={{A}_{1}}:{{T}_{1}}:{{G}_{1}}:{{X}_{1}}={{A}_{1}}:1,5{{A}_{1}}:2,5{{A}_{1}}:0,5{{A}_{1}}=1:1,5:2,5:0,5$.
a. Số nuclêôtit mỗi loại trên mạch 1 của đoạn ADN.
Áp dụng công thức giải nhanh, ta có:
${{A}_{1}}=\frac{a.H}{\left( 2a+2t+3g+3x \right)}=\frac{1\times 1288}{2\times 1+2\times 1,5+3\times 2,5+3\times 0,5}=\frac{1288}{2+3+7,5+1,5}=\frac{1288}{14}=92$.
${{T}_{1}}=\frac{t.H}{\left( 2a+2t+3g+3x \right)}=\frac{1,5\times 1288}{2\times 1+2\times 1,5+3\times 2,5+3\times 0,5}=\frac{1932}{2+3+7,5+1,5}=\frac{1932}{14}=138$.
${{G}_{1}}=\frac{g.H}{\left( 2a+2t+3g+3x \right)}=\frac{2,5\times 1288}{2\times 1+2\times 1,5+3\times 2,5+3\times 0,5}=\frac{3220}{2+3+7,5+1,5}=\frac{3220}{14}=230$.
${{X}_{1}}=\frac{x.H}{\left( 2a+2t+3g+3x \right)}=\frac{0,5\times 1288}{2\times 1+2\times 1,5+3\times 2,5+3\times 0,5}=\frac{644}{2+3+7,5+1,5}=\frac{644}{14}=46$.
– Số nuclêôtit mỗi loại trên mạch 1 là:
${{A}_{1}}=92;\,\,{{T}_{1}}=92\times 1,5=138$;
${{G}_{1}}=92\times 2,5=230;\,\,{{X}_{1}}=92\times 0,5=46$.
b. Số nuclêôtit mỗi loại của đoạn ADN.
$A=T={{A}_{1}}+{{T}_{1}}=92+138=230$.
$G=X={{G}_{1}}+{{X}_{1}}=230+46=276$.
Bài 8: Một phân tử ADN có tỉ lệ % các loại nuclêôtit trên mạch 1 là 15%A; 20%T; 32%G; 33%X. Hãy xác định tỉ lệ % các loại nuclêôtit của ADN.
Lời giải chi tiết
Công thức giải nhanh:
| Tỉ lệ % số nuclêôtit loại A của ADN bằng trung bình cộng tỉ lệ % số nuclêôtit của A và T trên một mạch.
$\%{{A}_{A\text{D}N}}=\frac{\%{{A}_{1}}+\%{{T}_{1}}}{2}$; $\,\%{{G}_{A\text{D}N}}=\frac{\%{{G}_{1}}+\%{{X}_{1}}}{2}$ |
Chứng minh:
Về số lượng, ta có ${{A}_{1}}+{{T}_{1}}={{A}_{A\text{D}N}}$.
Gọi N là tổng số nuclêôtit của cả ADN thì tổng số nuclêôtit trên một mạch $=\frac{N}{2}$
Ta có: $\%{{A}_{1}}+\%{{T}_{1}}=\frac{{{A}_{1}}}{N/2}+\frac{{{T}_{1}}}{N/2}=\frac{{{A}_{1}}+{{T}_{1}}}{N/2}=\frac{2\left( {{A}_{1}}+{{T}_{1}} \right)}{N}=\frac{2{{A}_{A\text{D}N}}}{N}=2.\%{{A}_{A\text{D}N}}$
$\to \%{{A}_{1}}+\%{{T}_{1}}=2.\%{{A}_{A\text{D}N}}\to \%{{A}_{A\text{D}N}}=\frac{\%{{A}_{1}}+\%{{T}_{1}}}{2}$.
$\%{{G}_{1}}+\%{{X}_{1}}=\frac{{{G}_{1}}}{N/2}+\frac{{{X}_{1}}}{N/2}=\frac{{{G}_{1}}+{{X}_{1}}}{N/2}=\frac{2\left( {{G}_{1}}+{{X}_{1}} \right)}{N}=\frac{2{{G}_{A\text{D}N}}}{N}=2.\%{{G}_{A\text{D}N}}$
$\to \%{{G}_{1}}+\%{{X}_{1}}=2.\%{{G}_{A\text{D}N}}\to \%{{G}_{A\text{D}N}}=\frac{\%{{G}_{1}}+\%{{X}_{1}}}{2}$.
Áp dụng công thức giải nhanh, ta có:
$\%{{A}_{A\text{D}N}}=\%{{T}_{A\text{D}N}}=\frac{\%{{A}_{1}}+\%{{T}_{1}}}{2}=\frac{15\%+20\%}{2}=17,5\%$.
$\%{{G}_{A\text{D}N}}=\%{{X}_{A\text{D}N}}=\frac{\%{{G}_{1}}+\%{{X}_{1}}}{2}=\frac{32\%+33\%}{2}=32,5\%$.
Bài tập vận dụng: Trên mạch hai của gen có tỉ lệ các loại nuclêôtit $A:T:G:X=1:3:2:4$. Hãy xác định tỉ lệ \% các loại nuclêôtit của gen.
Cách tính:
$\%{{A}_{A\text{D}N}}=\%{{T}_{A\text{D}N}}=\frac{\left( 1+3 \right)\times 100\%}{2\times \left( 1+3+2+4 \right)}=20\%$.
$\%{{G}_{A\text{D}N}}=\%{{X}_{A\text{D}N}}=\frac{\left( 2+4 \right)\times 100\%}{2\times \left( 1+3+2+4 \right)}=30\%$.
Bài 9*: Có một enzym cắt giới hạn cắt các đoạn ADN mạch kép ở đoạn trình tự nuclêôtit AGGXT. Khi sử dụng enzym này để cắt một phân tử ADN có tổng số ${{3.10}^{7}}$ cặp nuclêôtit (bp) thì theo lí thuyết phân tử ADN này sẽ bị cắt thành bao nhiêu đoạn ADN?
Lời giải chi tiết
Bước 1: Tìm tỉ lệ của các loại nuclêôtit liên quan đến bộ ba cần tính xác suất
Theo lí thuyết thì ở trong tự nhiên, tỉ lệ của 4 loại nuclêôtit ở trên ADN là tương đương nhau, mỗi loại chiếm tỉ lệ $=\frac{1}{4}$
Bước 2: Sử dụng toán tổ hợp để tính xác suất
– Đoạn trình tự AGGXT có 5 nuclêôtit nên có xác suất $={{\left( \frac{1}{4} \right)}^{5}}=\frac{1}{{{4}^{5}}}$.
– Có một enzym cắt giới hạn cắt các đoạn ADN mạch kép ở đoạn trình tự nuclêôtit AGGXT. Khi sử dụng enzym này để cắt một phân tử ADN có tổng số ${{3.10}^{7}}$ cặp nuclêôtit (bp) thì theo lí thuyết phân tử ADN này sẽ có số vị trí bị cắt là $=\frac{1}{{{4}^{5}}}\times {{3.10}^{7}}=29296,875\approx 29296$ (vị trí cắt).
– Với 29296 vị trí cắt thì sẽ có số đoạn ADN là $29296+1=29297$ đoạn.
