20 câu Trắc nghiệm Lũy thừa với số mũ tự nhiên của 1 số hữu tỉ (Kết nối tri thức) có đáp án 2025 – Toán lớp 7

Trắc nghiệm Toán 7 Bài 3: Lũy thừa với số mũ tự nhiên của 1 số hữu tỉ

I. Nhận biết

Câu 1. Trong số những khẳng định sau, khẳng định nào sai?

A. ${\text{x}}^{\text{m}}{\text{.x}}^{\text{n}}{\text{ = x}}^{m+n}$

B. ${\text{x}}^{\text{0}}\text{ = 1}$

C. ${\text{x}}^{\text{1}}\text{ = 1}$

D. $\frac{{\text{x}}^{\text{m}}}{{\text{x}}^{\text{n}}}{\text{ = x}}^{m-n}$  ( x ≠ 0; m ≥ n ).

Hướng dẫn giải

Đáp án: C

Giải thích: Theo quy ước:  với x ≠ 0; nên khẳng định sai là C.

Câu 2. Trong số những khẳng định sau, khẳng định nào sai?

A. ${\text{(x.y)}}^{\text{n}}{\text{ = x}}^{\text{n}}{\text{.y}}^{\text{n}}$  ;

B. ${\left(\frac{\text{x}}{\text{y}}\right)}^{\text{n}}\text{= }\frac{{\text{x}}^{\text{n}}}{{\text{y}}^{\text{n}}}$ ;

C. ${\text{x}}^{\text{m}}{\text{.x}}^{\text{n}}{\text{ = x}}^{\text{m.n}}$ ;

D. $\frac{{\text{x}}^{\text{m}}}{{\text{x}}^{\text{n}}}{\text{ = x}}^{m-n}$ ( x ≠ 0; m ≥ n ).

Hướng dẫn giải

Đáp án: C

Giải thích:

Theo định nghĩa: ${\text{x}}^{\text{m}}{\text{.x}}^{\text{n}}{\text{ = x}}^{m+n}$  nên khẳng định sai là khẳng định C.

Câu 3. Tính giá trị biểu thức ${\left(\frac{1}{2}\right)}^5.{\left(\frac{1}{2}\right)}^3$ .

A. $\frac{1}{2^{15}}$ ;

B. $\frac{1}{2^8}$ ;

C. $2^8$ ;

D. $\frac{1}{2^2}$ .

Hướng dẫn giải

Đáp án: B

Giải thích:

${\left(\frac{1}{2}\right)}^5.{\left(\frac{1}{2}\right)}^3={\left(\frac{1}{2}\right)}^{5+3}={\left(\frac{1}{2}\right)}^8=\frac{1}{2^8}$

Vậy đáp án đúng là B.

Câu 4. Tính giá trị biểu thức $8.{\left(2^3\right)}^4$

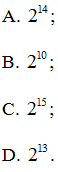
Hướng dẫn giải

Đáp án: C

Giải thích:

Theo quy ước: ${{\text{(x}}^{\text{m}}\text{)}}^{\text{n}}{\text{ = x}}^{\text{m.n}}$ và ${\text{x}}^{\text{m}}{\text{.x}}^{\text{n}}{\text{ = x}}^{m+n}$  nên ta có$8.{\left(2^3\right)}^4=2^3{.2}^{3.4}=2^{3+12}=2^{15}$

 Vậy đáp án đúng là C. 

Câu 5. Tính giá trị biểu thức $\frac{2^2{.7}^9}{4}$

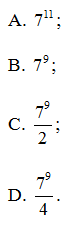
Hướng dẫn giải

Đáp án: B

Giải thích: Theo định nghĩa: ${\text{(x.y)}}^{\text{n}}{\text{ = x}}^{\text{n}}{\text{.y}}^{\text{n}}$ nên ta có $\frac{2^2{.7}^9}{4}=\frac{2^2{.7}^9}{2^2}=\frac{2^2{.7}^9}{2^2}=7^9$

Vậy đáp án đúng là B. 

II. Thông hiểu

Câu 1. Tính giá trị biểu thức A = ${\left(\frac{-1}{7}\right)}^5.{(-7)}^5-{2022}^0$

A. 0;

B. – 1;

C. 1;

D. 2.

Hướng dẫn giải

Đáp án: A

Giải thích:

Sử dụng ${\text{(x.y)}}^{\text{n}}{\text{ = x}}^{\text{n}}{\text{.y}}^{\text{n}}$ và ${\text{x}}^{\text{0}}\text{ = 1}$  ta có:

A = ${\left(\frac{-1}{7}\right)}^5.{(-7)}^5-{2022}^0={\left[\left(\frac{-1}{7}\right).\left(-7\right)\right]}^5-1=1^5-1=0.$

Vậy đáp án đúng là A.

Câu 2. Tìm x sao cho ${182}^{\text{x}}{\text{: 13}}^{\text{x}}\text{ = 196 }$ .

A. 0;

B. -1;

C. 2;

D. 1.

Hướng dẫn giải

Đáp án: C

Giải thích: 

Câu 3. Tính giá trị biểu thức $\text{A}=\frac{4^6{.9}^5}{8^4{.3}^9}$

A. 3;

B. $\frac{2}{3}$ ;

C. $\frac{3}{2}$ ;

D. $\frac{4}{3}$ .

Hướng dẫn giải

Đáp án: A

Giải thích:

Ta có: $\text{A}=\frac{4^6{.9}^5}{8^4{.3}^9}=\frac{{\left(2^2\right)}^6{.3}^{10}}{{\left(2^3\right)}^4{.3}^9}=\frac{2^{12}{.3}^{10}}{2^{12}{.3}^9}=3$

Vậy đáp án đúng là A.

Câu 4. Cho (x + 1)⁵ = – 32

A. x = 1;

B. x = 2;

C. x = – 3;

D. Không tồn tại x.

Hướng dẫn giải

Đáp án: D

Giải thích:

Xét phương trình (x + 1)⁵ = – 32

⇔ (x + 1)⁵ = ( – 2)⁵

⇔ x + 1 =  – 2

⇔ x =  – 2 – 1

⇔ x =  – 3

Vậy x =  – 3.

Câu 5. Cho biểu thức 2^x + 3x – (7^x)³. Giá trị của biểu thức khi x = 1.

A. – 338;

B. – 16 802;

C. – 2,5;

D. – 478.

Hướng dẫn giải

Đáp án: A

Giải thích:

Thay x = 1 vào biểu thức 2^x + 3x – (7^x)³  ta được: 2¹ + 3.1 – (7¹)³  =  – 338.

Vậy giá trị biểu thức khi x = 1 là – 338.

Câu 6. Tìm số tự nhiên n thỏa mãn 6ⁿ + 6ⁿ⁺³ = 217

A. 1;

B. 2;

C. -1;

D. 0.

Hướng dẫn giải

Đáp án: D

Giải thích:

6ⁿ + 6ⁿ⁺³ = 217

⇔ 6ⁿ + 6ⁿ.6³ = 217

⇔ 6ⁿ.(1 + 6³) = 217

⟺  ${\text{6}}^{\text{n}}\text{ = }\frac{\text{217}}{{\text{1+6}}^{\text{3}}}\text{ = 1}$

⟺ n = 0.

Vậy đáp án đúng là D.

Câu 7. Cho hai biểu thức A = 7²  và B = 2² + 3² + 6². Nhận xét nào dưới đây là đúng:

A. A > B;

B. A < B;

C. A = 2B;

D. A = B.

Hướng dẫn giải

Đáp án: D

Giải thích:

Ta có: B = 2² + 3² + 6² = 4 + 9 + 36 = 49 = 7² = A.

Suy ra A = B.

Vậy đáp án đúng là D.

III. Vận dụng

Câu 1. Tính giá trị biểu thức A = $1-\frac{3}{4}+{\left(\frac{3}{4}\right)}^2-{\left(\frac{3}{4}\right)}^3+{\left(\frac{3}{4}\right)}^4-\mathrm{\dots }-{\left(\frac{3}{4}\right)}^{2021}+{\left(\frac{3}{4}\right)}^{2022}$

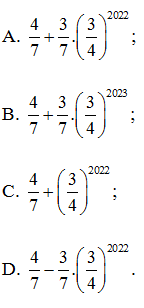
Hướng dẫn giải

Đáp án: A

Giải thích: 

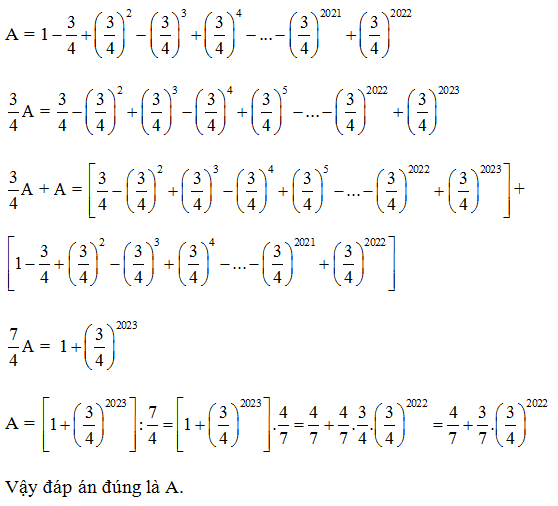
Câu 2. Tính giá trị biểu thức H = $1+2.6+{3.6}^2+{4.6}^3+\mathrm{\dots }+{100.6}^{99}$

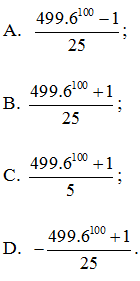
Hướng dẫn giải

Đáp án: B

Giải thích:

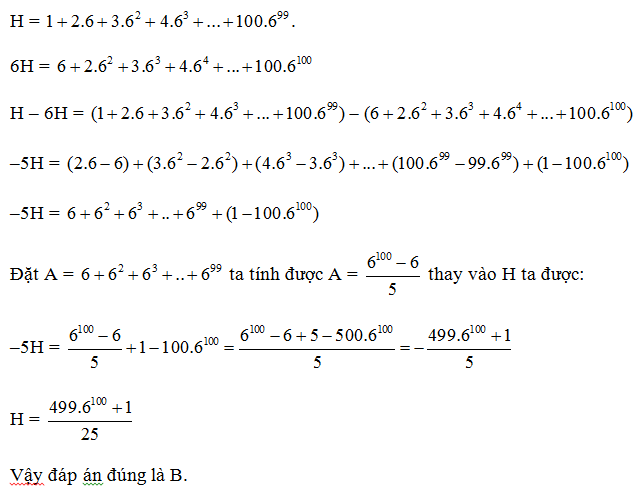
Câu 3. Tính giá trị biểu thức M = $2^{50}-2^{49}-2^{48}-\mathrm{\dots }-2^3-2^2-2$

A. 0;

B. 1;

C. -1;

D. 2.

Hướng dẫn giải

Đáp án: D

Giải thích: 

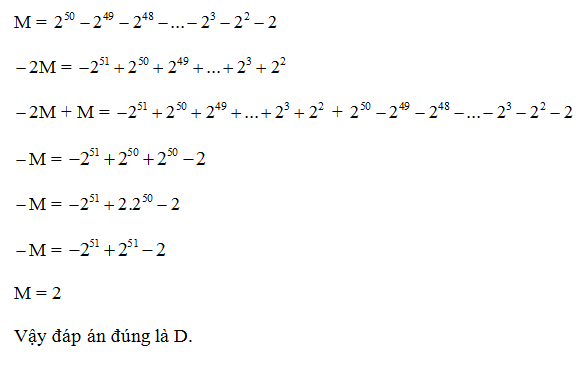
Xem thêm các bài trắc nghiệm Toán 7 Kết nối tri thức hay, chi tiết khác:

Trắc nghiệm Cộng, trừ, nhân, chia số hữu tỉ

Trắc nghiệm Lũy thừa với số mũ tự nhiên của 1 số hữu tỉ

Trắc nghiệm Thứ tự thực hiện các phép tính. Quy tắc chuyển vế

Trắc nghiệm Bài ôn tập cuối chương 1

Trắc nghiệm Làm quen với số thập phân vô hạn tuần hoàn