Giải SBT Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết
Giải SBT Toán 7 trang 39 Tập 1
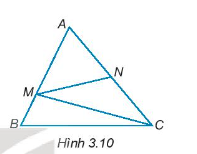
Bài 3.9 trang 39 Toán 7 Tập 1: Cho Hình 3.10.
a) Viết tên góc so le trong với góc NMC.
b) Viết tên góc đồng vị với góc ACB, góc AMN.
Lời giải:
a) Góc so le trong với góc NMC là góc MCB.
b) Góc đồng vị với góc ACB là góc ANM;
Góc đồng vị với góc AMN là góc ABC.
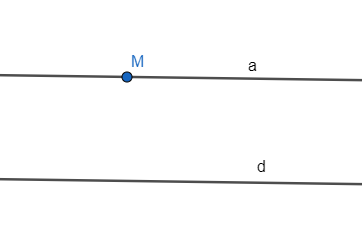
Bài 3.10 trang 39 Toán 7 Tập 1: Vẽ đường thẳng d và điểm M không thuộc d. Vẽ đường thẳng a đi qua M và song song với d.
Lời giải:
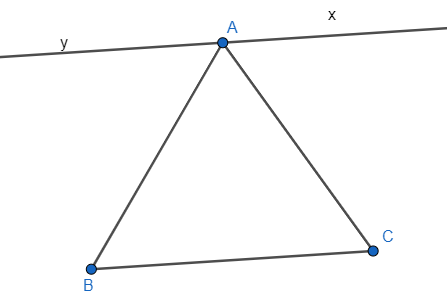
Bài 3.11 trang 39 Toán 7 Tập 1: Vẽ tam giác ABC bất kì. Vẽ đường thẳng xy đi qua điểm A và song song với BC.
Lời giải:
Bài 3.12 trang 39 Toán 7 Tập 1: Vẽ lại Hình 3.11 vào vở rồi giải thích tại sao xx’ // yy’.
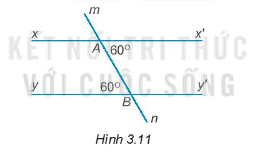
Lời giải:
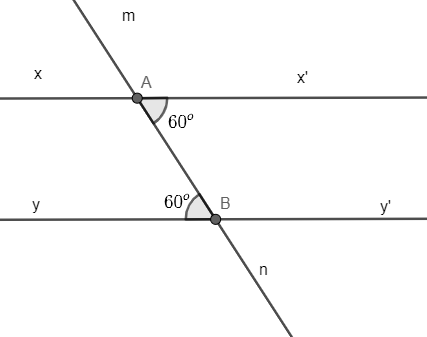
Ta có: Góc x’An và góc mBy là hai góc so le trong
Mặt khác
Do đó, hai đường thẳng xx’ và yy’ song song với nhau.
Bài 3.13 trang 39 Toán 7 Tập 1: Cho Hình 3.12. Giải thích tại sao a // b.
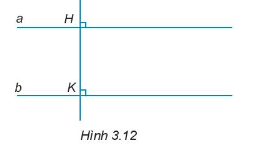
Lời giải:
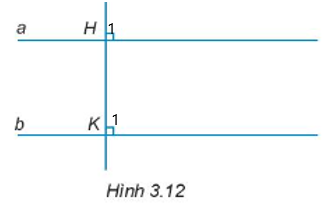
Vì HK vuông góc với a nên ;
Vì HK vuông góc với b nên .
Mà là hai góc đồng vị.
Do đó, a // b.
Giải SBT Toán 7 trang 40 Tập 1
Bài 3.14 trang 40 Toán 7 Tập 1: Cho Hình 3.13. Giải thích tại sao MN // PQ.
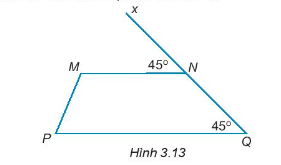
Lời giải:
Đường thẳng QN cắt đường thẳng MN và PQ lần lượt tại N và Q.
Từ hình vẽ ta thấy: ;
Mà hai góc này ở vị trí đồng vị.
Do đó MN // PQ.
Bài 3.15 trang 40 Toán 7 Tập 1: Cho Hình 3.14. Giải thích tại sao EF // NP.
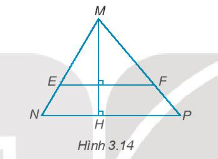
Lời giải:
Từ hình vẽ ta thấy:
MH vuông góc với NP; MH vuông góc với EF nên EF // NP (quan hệ từ vuông góc đến song song).
Bài 3.16 trang 40 Toán 7 Tập 1: Vẽ lại hình 3.15 vào vở, biết NP // MQ và NP = MQ.
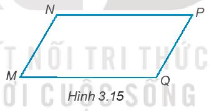
Lời giải:
Bài 3.17 trang 40 Toán 7 Tập 1: Vẽ lại Hình 3.16 vào vở. Giải thích tại sao Hx //Ky.
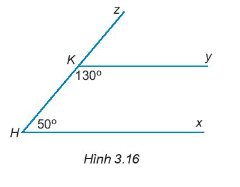
Lời giải:
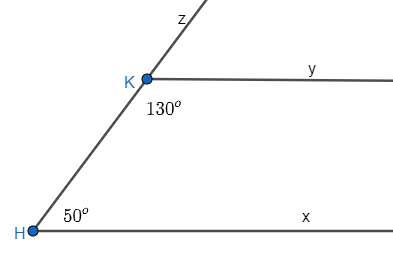
Vì góc và góc là hai góc kề bù.
Do đó, + = 180o
Thay số: + 130o = 180o
= 180o – 130o
= 50o.
Vì và là hai góc đồng vị và = = 50o.
Do đó, Ky // Hx.
Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc
Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết
Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song
Bài 11: Định lí và chứng minh định lí
Ôn tập chương 3
Lý thuyết Hai đường thẳng song song và dấu hiệu nhận biết
1. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
• Cho đường thẳng c cắt hai đường thẳng a và b lần lượt tại A và B tạo thành bốn góc đỉnh A và bốn góc đỉnh B. Khi đó ta có:
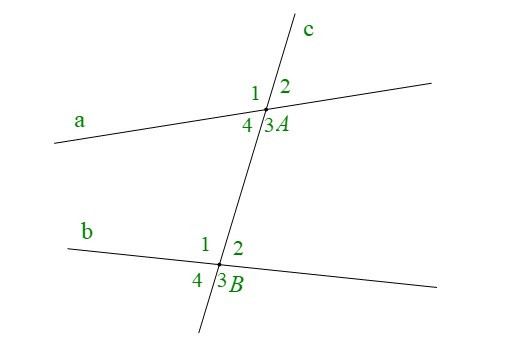
+ Các cặp góc so le trong là: A3 và B1; A4 và B2.
+ Các cặp góc đồng vị là: A1 và B1; A2 và B2; A3 và B3; A4 và B4.
+ Các cặp góc trong cùng phía là: A4 và B1; A3 và B2.
• Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
+ Hai góc so le trong còn lại bằng nhau.
+ Hai góc đồng vị bằng nhau.
Ví dụ:
+ Cho đường thẳng c cắt hai đường thẳng phân biệt a, b lần lượt tại A và B.
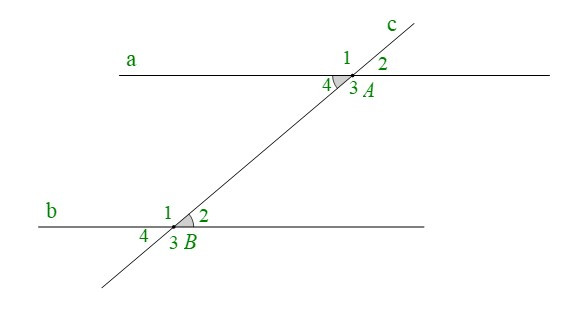
Ta có là cặp góc so le trong
Nếu thì cặp góc so le trong còn lại và các cặp góc đồng vị bằng nhau:
2. Dấu hiệu nhận biết hai đường thẳng song song
• Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng nhau thì a và b song song với nhau. Kí hiệu là: .
• Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Ví dụ:
+ Cho hình vẽ:
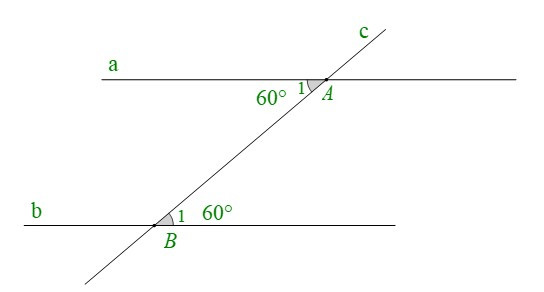
Ta có: . Mà hai góc ở vị trí so le trong.
Do đó: (dấu hiệu nhận biết hai đường thẳng song song).
+ Cho hình vẽ:
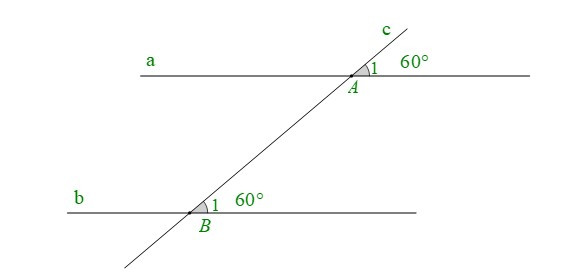
Ta có: . Mà hai góc ở vị trí đồng vị.
Do đó: (dấu hiệu nhận biết hai đường thẳng song song).
+ Cho hình vẽ:
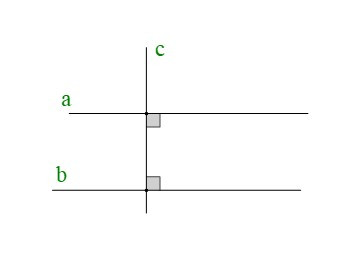
Ta có: và
Do đó: .
Chú ý:
+ Muốn vẽ đường thẳng đi qua một điểm và song song với một đường thẳng cho trước bằng góc 60° của êke ta làm như sau:
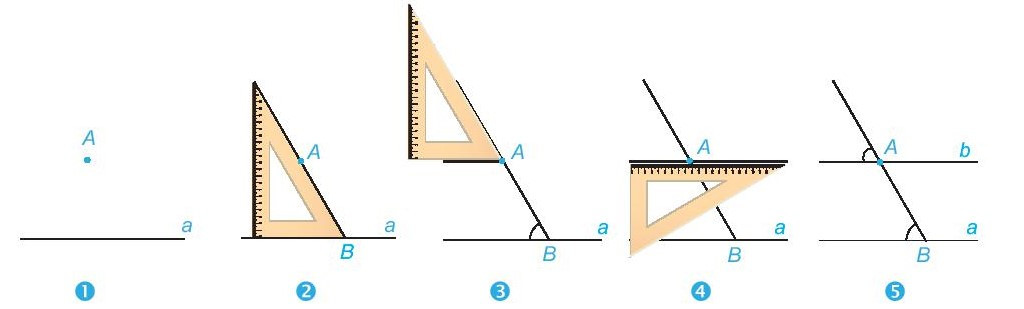
+ Tương tự ta có thể dùng góc vuông hoặc góc 30° của êke (thay cho góc 60°) để vẽ đường thẳng đi qua một điểm và song song với đường thẳng cho trước.