Giải SBT Toán lớp 8 Bài 27: Khái niệm hàm số và đồ thị của hàm số
Giải SBT Toán 8 trang 26
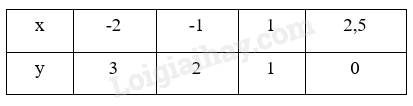
Bài tập 7.17 trang 26 SBT Toán 8 Tập 2: Các giá trị tương ứng của hai đại lượng x và y cho bởi các bảng dưới đây. Đại lượng y có phải là một hàm số của x không ?
a)
b)
Lời giải:
a) y là hàm số của x. Do với mỗi giá trị x thì chỉ cho một giá trị y tương ứng.
b) y không là hàm số của x. Do với giá trị x = 1 thì cho hai giá trị y tương ứng là y = 1 và y = 2.
Bài tập 7.18 trang 26 SBT Toán 8 Tập 2: Mối quan hệ giữa số tháng tuổi x (tháng) và cân nặng y (kg) của một em bé trong 6 tháng đầu đời được cho bởi bảng sau:
Hỏi cân nặng y của em bé đó có phải là hàm số của số tháng tuổi x không ?
Hãy xác định cân nặng của em bé đó lúc 4 tháng tuổi.
Lời giải:
Cân nặng y của em bé đó là hàm số của số tháng tuổi x. Vì với mỗi giá trị của tháng tuổi x chỉ có một giá trị cân nặng y tương ứng.
Em bé lúc 4 tháng tuổi tức là x = 4 thì cân nặng tương ứng là y = 6,2 (kg).
Bài tập 7.19 trang 26 SBT Toán 8 Tập 2: Cho hàm số y = f(x) = 2x2 – 1
a) Tính f(0); f(–1).
b) Hoàn thành bảng sau:
c) Tìm tất cả các giá trị x sao cho y = 17.
Lời giải:
a) Ta có: f(0) = 2.02 – 1 = –1 ; f(–1) = 2.(–1)2 – 1 = 1.
b)
Ta có:
Tại x = –2 thì f(–2) = 2.(–2)2 – 1 = 7
Tại x = –1 thì f(–1) = 1
Tại x = 0 thì f(0) = –1
Tại x = 1 thì f(1) = 2.12 – 1 = 1
Tại x = 2 thì f(2) = 2.22 – 1 = 7
Do đó, ta có bảng sau:
c) Ta có y = 17, tức là 2x2 – 1 = 17 hay x2 = 9, suy ra x = – 3 hoặc x = 3.
Vậy khi x = – 3 hoặc x = 3 thì y = 17.
Bài tập 7.20 trang 26 SBT Toán 8 Tập 2: a) Xác định tọa độ của các điểm A, B, C, D trong hình bên.
b) Xác định các điểm E(0; – 1) và F(–2; 3) trong hình bên.
Lời giải:
a) Từ hình vẽ ta thấy:
Tọa độ của điểm A là A(– 3; 4);
Tọa độ của điểm B là B(–2; –2);
Tọa độ của điểm C là C(1; –3);
Tọa độ của điểm D là D(3; 0).
b) Các điểm E và F được biểu diễn trên hình dưới đây.
Giải SBT Toán 8 trang 27
Bài tập 7.21 trang 27 SBT Toán 8 Tập 2: Hàm số y = f(x) được cho trong bảng sau:
Vẽ đồ thị của hàm số y = f(x).
Lời giải:
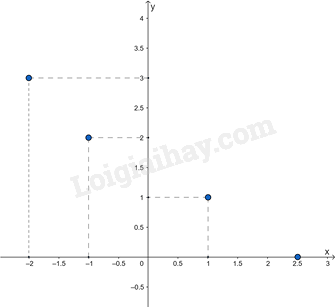
Đồ thị hàm số đã cho gồm các điểm: A(–2; 6), B(–1; 3), O(0; 0), C(1; –3) và D(2; –6).
Vẽ hệ trục tọa độ Oxy và xác định các điểm A, B, O, C, D. Ta có đồ thị hàm số như hình dưới:
Bài tập 7.22 trang 27 SBT Toán 8 Tập 2: Hệ thức y2 + x2 = 1 có xác định một hàm số y = f(x) không ? Vì sao ?
Lời giải:
Ta có: y2 + x2 = 1
Với x = ta có: y2 + = 1 nên y2 =
Suy ra .
Do đó, với một giá trị x =có hai giá trị y tương ứng.
Vậy hệ thức y2 + x2 = 1 không xác định một hàm số y = f(x).
Bài tập 7.23 trang 27 SBT Toán 8 Tập 2: Hãy biểu thị diện tích S của hình chữ nhật dưới dạng một hàm số của chiều dài x nếu chiều dài của hình chữ nhật gấp đôi chiều rộng.
Lời giải:
Chiều dài hình chữ nhật là x (x > 0).
Do chiều dài của hình chữ nhật gấp đôi chiều rộng nên chiều rộng của hình chữ nhật là 0,5x.
Diện tích của hình chữ nhật là: 0,5x.x = 0,5x2
Vậy hàm số biểu thị diện tích S theo chiều dài là: S(x) = 0,5x2.
Bài tập 7.24 trang 27 SBT Toán 8 Tập 2: Đồ thị sau biểu diễn vận tốc xe máy v (tính bằng km/h) của anh Nam dưới dạng một hàm số của thời gian t (tính bằng phút).
Dựa vào đồ thị trên, hãy trả lời các câu hỏi sau:
a) Anh Nam đi nhanh nhất trong khoảng thời gian nào ?
b) Vận tốc của anh Nam bằng 0 trong khoảng thời gian nào ?
c) Vận tốc của anh Nam trong khoảng thời gian từ 2 phút đến 4 phút là bao nhiêu ?
d) Trong khoảng thời gian nào anh Nam đi với vận tốc 38 km/h ?
Lời giải:
a) Anh Nam đi nhanh nhất trong khoảng thời gian từ 7 phút đến 7,4 phút.
b) Vận tốc của anh Nam bằng 0 trong khoảng thời gian từ 4,2 phút đến 6 phút.
c) Vận tốc của anh Nam trong khoảng thời gian từ 2 phút đến 4 phút là 30 km/h.
d) Trong khoảng thời gian từ 7,6 phút đến 8 phút thì anh Nam đi với vận tốc 38 km/h.
Xem thêm giải sách bài tập Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
Bài 26: Giải bài toán bằng cách lập phương trình
Bài 27: Khái niệm hàm số và đồ thị của hàm số
Bài 28: Hàm số bậc nhất và đồ thị của hàm số bậc nhất
Bài 29: Hệ số góc của đường thẳng
Bài tập cuối chương 7
Lý thuyết Khái niệm hàm số và đồ thị của hàm số
1. Hàm số
Khái niệm:
Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số.
Ví dụ: Ta có bảng nhiệt độ dự báo ở Thủ đô Hà Nội ngày 25/5/2023.
t(h) | 10 | 11 | 12 | 13 |
T(0C) | 32 | 33 | 34 | 34 |
Ta có nhiệt độ T là hàm số của thời điểm t vì mỗi giá trị của t chỉ xác định đúng một giá trị của T.
Ngược lại, thời điểm t không phải là hàm số của nhiệt độ T, vì nhiệt độ T = 340C tương ứng với hai thời điểm khác nhau t = 12 và t = 13.
Chú ý: Khi y là hàm số của x, ta viết
Ví dụ: Cho hàm số y = f(x) = x + 3.
f(-2) = -2 + 3 = 1; f(0) = 0 + 3 = 3
2. Mặt phẳng tọa độ
Khái niệm: Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ.
- Ox nằm ngang gọi là trục hoành;
- Oy thẳng đứng gọi là trục tung;
- O gọi là gốc tọa độ.
Tọa độ của một điểm:
Trong mặt phẳng tọa độ, mỗi điểm M xác định duy nhất một cặp số và mỗi cặp số xác định duy nhất một điểm M.
Cặp số gọi là tọa độ của M, kí hiệu là M(x0,y0), trong đó x0 là hoành độ, y0 là tung độ của điểm M.
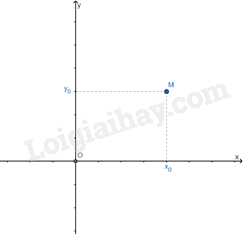
Ví dụ: Điểm M có tọa độ là (2; -3), kí hiệu là M(2; -3). Số 2 gọi là hoành độ, số -3 gọi là tung độ của điểm M.
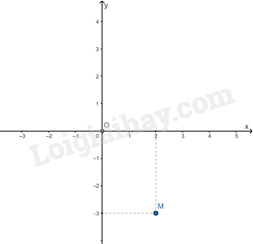
3. Đồ thị của hàm số
Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng (x; y) trên mặt phẳng tọa độ.
Ví dụ: Đồ thị của hàm số y = f(x) cho bởi bảng: