I. Khái niệm tích phân
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right],F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\) trên đoạn \(\left[ {a;b} \right]\). Hiệu \(F\left( b \right) – F\left( a \right)\) được gọi là tích phân của \(f\) từ \(a\) đến \(b\). Kí hiệu:
$I = \int\limits_a^b {f\left( x \right)dx} = \left. {F\left( x \right)} \right|_a^b = F\left( b \right) – F\left( a \right)$
II. Tính chất tích phân
Giả sử các hàm số \(f,g\) liên tục trên \(\left[ {a;b} \right],c\) là điểm bất kì thuộc \(\left[ {a;b} \right]\). Khi đó ta có:
a) \(\int\limits_a^a {f\left( x \right)dx} = 0\)
b) \(\int\limits_a^b {f\left( x \right)dx} = – \int\limits_b^a {f\left( x \right)dx} \)
c) \(\int\limits_a^b {k.f\left( x \right)dx} = k.\int\limits_a^b {f\left( x \right)dx} \)
d) \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^b {f\left( t \right)dt} \)
e) \(\int\limits_a^b {f\left( x \right)dx} + \int\limits_b^c {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} ;\) \(\forall b \in \left[ {a;c} \right]\)
f) \(\int\limits_a^b {\left[ {f\left( x \right) \pm g\left( x \right)} \right]dx} \) \(= \int\limits_a^b {f\left( x \right)dx} \pm \int\limits_a^b {g\left( x \right)dx} \)
g) Nếu \(f\left( x \right) \ge 0\) thì \(\int\limits_a^b {f\left( x \right)dx} \ge 0\)
h) Nếu \(f\left( x \right) \ge g\left( x \right)\) trên \(\left[ {a;b} \right]\) thì \(\int\limits_a^b {f\left( x \right)dx} \ge \int\limits_a^b {g\left( x \right)dx} \).
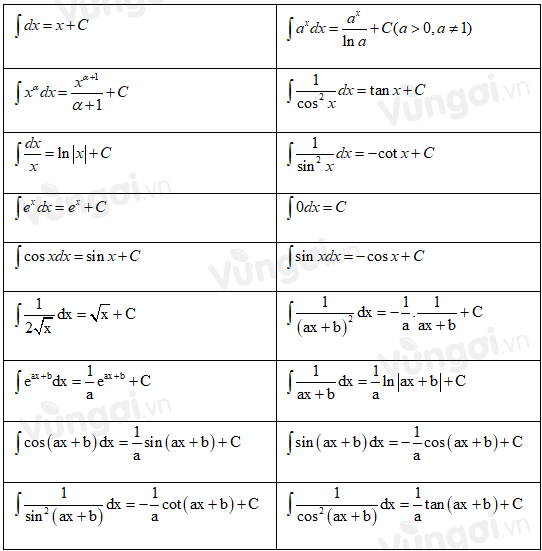
III. Bảng nguyên hàm