I. Một số công thức cần nhớ để đổi biến trong tích phân
– Vi phân:
\(\begin{array}{l}t = u\left( x \right) \Rightarrow dt = u’\left( x \right)dx\\u\left( t \right) = v\left( x \right) \Rightarrow u’\left( t \right)dt = v’\left( x \right)dx\end{array}\)
– Công thức đổi biến: \(\int\limits_a^b {f\left[ {u\left( x \right)} \right]u’\left( x \right)dx} = \int\limits_{t\left( a \right)}^{t\left( b \right)} {f\left( t \right)dt} \)
II. Khoảng cách giữa đường thẳng và mặt phẳng song song
– Khoảng cách giữa đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) song song với \(a\) là khoảng cách từ một điểm nào của \(a\) đến mặt phẳng \(\left( P \right)\).
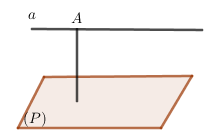
Kí hiệu: \(d\left( {a,\left( P \right)} \right) = d\left( {A,\left( P \right)} \right)\) trong đó \(A\) là một điểm nào đó nằm trên đường thẳng \(a\).
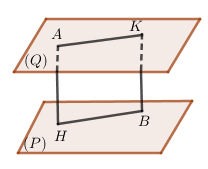
III. Khoảng cách giữa hai mặt phẳng song song
– Khoảng cách giữa hai mặt phẳng là khoảng cách từ một điểm bất kì từ mặt phẳng này đến mặt phẳng kia.
Kí hiệu: \(d\left( {\left( P \right),\left( Q \right)} \right) = d\left( {A,\left( P \right)} \right) = d\left( {B,\left( Q \right)} \right)\) trong đó \(A\) là một điểm nào đó nằm trong \(\left( Q \right)\) và \(B\) là một điểm nào đó nằm trong \(\left( P \right)\).