20 câu Trắc nghiệm Tổng các góc trong một tam giác (Kết nối tri thức) có đáp án 2025 – Toán lớp 7

Trắc nghiệm Toán 7 Bài 12:Tổng các góc trong một tam giác

I. Nhận biết

Câu 1. Hai góc phụ nhau là:

A. Hai góc có số đo không nhỏ hơn 90°;                 

B. Hai có tổng số đo bằng 180°;                     

C. Hai góc có giá trị tuyệt đối của hiệu số đo bằng 90°;             

D. Hai góc có tổng số đo bằng 90°.

Hướng dẫn giải

Đáp án: D

Giải thích:

Hai góc có tổng số đo bằng 90° được gọi là hai góc phụ nhau.

Hai góc có tổng số đo bằng 180° được gọi là hai góc bù nhau.

Vậy ta chọn phương án D.

Câu 2. Tam giác có một góc lớn hơn 90° là:

A. Tam giác nhọn;                       

B. Tam giác tù;                  

C. Tam giác vuông;                      

D. Đáp án khác.

Hướng dẫn giải

Đáp án: B

Giải thích:

Tam giác có một góc tù (tức là góc đó lớn hơn 90°) thì được gọi là tam giác tù.

Vậy ta chọn phương án B.

Câu 3. Tổng ba góc trong một tam giác bất kì luôn bằng:

A. 90°;                      

B. 180°;                   

C. 270°;                   

D. 360°.

Hướng dẫn giải

Đáp án: B

Giải thích:

Vì tổng ba góc trong một tam giác luôn bằng 180°.

Nên ta chọn phương án B.

Câu 4. Tam giác nhọn là tam giác:

A. Có cả ba góc đều nhỏ hơn 90°;                  

B. Có một góc bất kì bằng 90°;            

C. Có một góc bất kì lớn hơn 90°;                  

D. Cả ba góc đều nhỏ hơn 180°.

Hướng dẫn giải

Đáp án: A

Giải thích:

Tam giác có ba góc đều nhọn (tức là ba góc đều nhỏ hơn 90°) được gọi là tam giác nhọn.

Vậy ta chọn phương án A.

Câu 5. Cho ∆ABC vuông tại B. Kết luận nào sau đây sai?

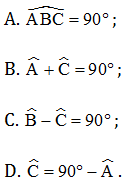
Hướng dẫn giải

Đáp án: C

Giải thích:

⦁ Vì ∆ABC vuông tại B nên ta có $\widehat{ABC}=90°$.

Do đó phương án A đúng.

⦁ Ta có ∆ABC vuông tại B.

Suy ra $\widehat{A}+\widehat{C}=90°$.

Do đó $\widehat{C}=90°-\widehat{A}$.

Vì vậy phương án B, D đúng.

Suy ra phương án C sai.

Vậy ta chọn phương án C.

II. Thông hiểu

Câu 1. Cho ∆ABC có $\widehat{B}=30°$, $\widehat{C}=40°$. Khi đó ∆ABC là:

A. Tam giác tù;                  

B. Tam giác nhọn;                       

C. Tam giác vuông;                      

D. Đáp án khác.

Hướng dẫn giải

Đáp án: A

Giải thích:

∆ABC có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc trong một tam giác)

Suy ra $\widehat{A}=180°-\widehat{B}-\widehat{C}=180°-30°-40°=110°>90°$.

Vì vậy $\widehat{A}$ là góc tù.

Do đó ∆ABC là tam giác tù.

Vậy ta chọn phương án A.

Câu 2. Kết luận nào sau đây đúng?

A. Một tam giác chỉ có tối đa hai góc nhọn;

B. Một tam giác chỉ có nhiều nhất một góc tù;      

C. Trong một tam giác, có ít nhất hai góc có số đo nhỏ hơn 60°;                   

D. Trong một tam giác, số đo của mỗi góc luôn nhỏ hơn tổng số đo các góc còn lại.

Hướng dẫn giải

Đáp án: B

Giải thích:

⦁ Ta có định nghĩa: Tam giác có ba góc đều nhọn được gọi là tam giác nhọn.

Do đó một tam giác có thể có ba góc nhọn.

Vì vậy phương án A sai.

⦁ Giả sử ∆ABC có $\widehat{A}, \widehat{B}$ là góc tù. Tức là, $\widehat{A}>90°,\widehat{B}>90°$.

Khi đó $\widehat{A}+\widehat{B}>180°$ (mâu thuẫn với định lí tổng ba góc của một tam giác).

Suy ra một tam giác chỉ có thể có một góc tù.

Vì vậy phương án B đúng.

⦁ Giả sử ∆ABC có $\widehat{A}<60°,\widehat{B}<60°,\widehat{C}<60°$.

Khi đó $\widehat{A}+\widehat{B}+\widehat{C}<60°+60°+60°=180°$ (mâu thuẫn với định lí tổng ba góc của một tam giác).

Suy ra, trong một tam giác, có nhiều nhất hai góc có số đo nhỏ hơn 60°.

Vì vậy phương án C sai.

⦁ Giả sử ∆ABC có $\widehat{A}$ tù.

Khi đó góc ngoài tại đỉnh A của ∆ABC là góc nhọn.

Tức là, tổng $\widehat{B}+\widehat{C}$ luôn luôn nhỏ hơn 90°.

Mà $\widehat{A}>90°$.

Vì vậy $\widehat{A}>90°>\widehat{B}+\widehat{C}$ (mâu thuẫn với kết luận ở phương án D).

Do đó phương án D sai.

Vậy ta chọn phương án B.

Câu 3. ∆ABC có $\widehat{A}=75°$, $\widehat{B}=45°$. Khi đó $\widehat{C}$ có số đo bằng:

A. 90°;                      

B. 60°;                      

C. 45°;                      

D. 75°.

Hướng dẫn giải

Đáp án: B

Giải thích:

∆ABC có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc trong một tam giác)

Suy ra $\widehat{C}=180°-\widehat{A}-\widehat{B}=180°-75°-45°=60°$.

Vậy ta chọn phương án B.

Câu 4. Cho ∆MNP có $\widehat{M}=80°$, biết $\widehat{N}-\widehat{P}=40°$. Khi đó số đo của $\widehat{N}$ bằng:

A. 75°;                      

B. 45°;                      

C. 70°;                      

D. 60°.

Hướng dẫn giải

Đáp án: C

Giải thích: 

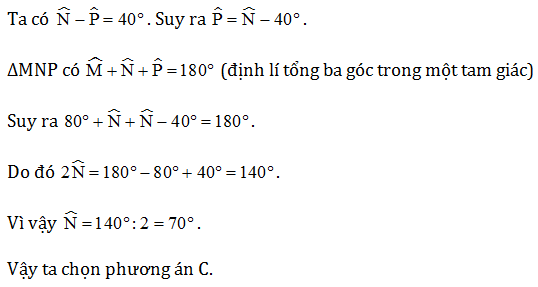
Câu 5. Cho ∆ABC có $\widehat{A}=75°$ và $\widehat{B}=2\widehat{C}$ . Số đo của $\widehat{C}$ bằng:

A. 70°;                      

B. 35°;                      

C. 40°;                      

D. 50°.

Hướng dẫn giải

Đáp án: B

Giải thích:

∆ABC có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc trong một tam giác)

Suy ra $75°+2\widehat{C}+\widehat{C}=180°$.

Do đó $3\widehat{C}=180°-75°=105°$.

Vì vậy $\widehat{C}=105°:3=35°$.

Vậy ta chọn phương án B.

Câu 6. Cho hình vẽ bên.

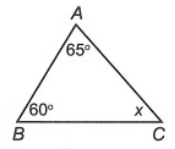
Số đo của x bằng:

A. 60°;                      

B. 30°;                      

C. 45°;                      

D. 55°.

Hướng dẫn giải

Đáp án: D

Giải thích:

∆ABC có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc trong một tam giác)

Suy ra 65° + 60° + x = 180°

Do đó x = 180° – 65° – 60° = 55°.

Vậy ta chọn phương án D.

Câu 7. Cho hình vẽ bên.

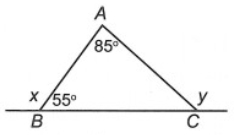
Số đo của x và y là:

A. x = 140° và y = 125°;            

B. x = 55° và y = 40°;                 

C. x = 125° và y = 140°;            

D. x = 40° và y = 55°.

Hướng dẫn giải

Đáp án: C

Giải thích:

⦁ Ta có y được gọi là góc ngoài tại đỉnh C của ∆ABC.

Suy ra $y=\widehat{BAC}+\widehat{ABC}=85°+55°=140°$.

⦁ Lại có: $x+\widehat{B}=180°$ (hai góc kề bù)

Suy ra $x=180°-\widehat{B}=180°-55°=125°$.

Vậy x = 125° và y = 140°.

Do đó ta chọn phương án C.

III. Vận dụng

Câu 1. Cho ∆MNP. Các đường phân giác trong các $\widehat{M}$, $\widehat{P}$ cắt nhau tại I. Kết luận nào sau đây đúng?

Hướng dẫn giải

Đáp án: A

Giải thích:

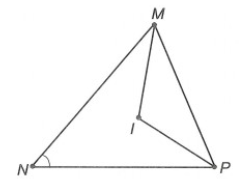
Ta có:

⦁ $\widehat{IMP}=\frac{1}{2}\widehat{NMP}$ (do MI là phân giác của $\widehat{NMP}$);

⦁ $\widehat{IPM}=\frac{1}{2}\widehat{NPM}$ (do PI là phân giác của $\widehat{NPM}$).

∆MIP có: $\widehat{MIP}+\widehat{IMP}+\widehat{IPM}=180°$ (định lí tổng ba góc trong một tam giác)

Suy ra $\widehat{MIP}=180°-\widehat{IMP}-\widehat{IPM}$

$=180°-\frac{1}{2}\widehat{NMP}-\frac{1}{2}\widehat{NPM}=180°-\frac{1}{2}\left(\widehat{NMP}+\widehat{NPM}\right)$   (1)

∆MNP có: $\widehat{MNP}+\widehat{NMP}+\widehat{NPM}=180°$ (định lí tổng ba góc trong một tam giác)

Suy ra $\widehat{NMP}+\widehat{NPM}=180°-\widehat{MNP}$    (2)

Thế (2) vào (1) ta được: $\widehat{MIP}=180°-\frac{1}{2}\left(180°-\widehat{MNP}\right)=90°+\frac{\widehat{MNP}}{2}$.

Vậy ta chọn phương án A.

Câu 2. Cho ∆ABC có $\widehat{B}=20°$, $\widehat{C}=40°$. Gọi AD là tia nằm giữa hai tia AB và AC sao cho $\widehat{CAD}=2\widehat{BAD}$. Số đo của $\widehat{ADC}$ bằng:

A. 10°;                      

B. 30°;                      

C. 45°;                      

D. 60°.

Hướng dẫn giải

Đáp án: D

Giải thích:

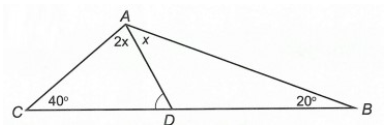
Vậy đáp án đúng là D

Câu 3. Cho ∆ABC vuông tại A. Kẻ AH vuông góc với BC (H ∈ BC). Các tia phân giác của $\widehat{ABC}$ và $\widehat{HAC}$ cắt nhau tại I. Khi đó ∆AIB là:

A. Tam giác vuông tại I;             

B. Tam giác vuông tại B;                       

C. Tam giác nhọn;            

D. Tam giác tù.

Hướng dẫn giải

Đáp án: A

Giải thích:

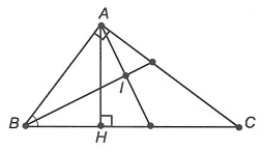
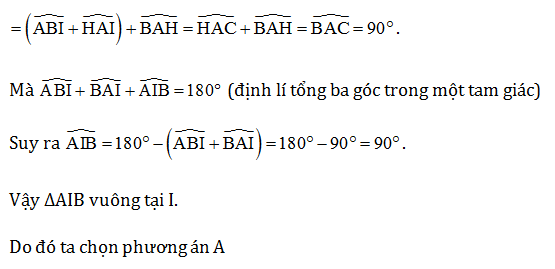
Xem thêm các bài trắc nghiệm Toán 7 Kết nối tri thức hay, chi tiết khác:

Trắc nghiệm Bài ôn tập cuối chương 3

Trắc nghiệm Tổng các góc trong một tam giác

Trắc nghiệm Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác

Trắc nghiệm Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Trắc nghiệm Các trường hợp bằng nhau của tam giác vuông