I. Định nghĩa và tính chất
+ Định nghĩa: \(\int {f(x)dx = F(x) + C \Leftrightarrow F'(x) = f(x)} \)
+ Tính chất:
1/ \(\int {f'(x)dx = f(x) + C} \)
2/\(\int {kf(x)dx = k\int {f(x)dx} } \) với \(\forall k \ne 0\).
3/ \(\int {\left[ {f(x) \pm g(x)} \right]dx = } \int {f(x)dx} \pm \int {g(x)dx} \)
II. Bảng nguyên hàm
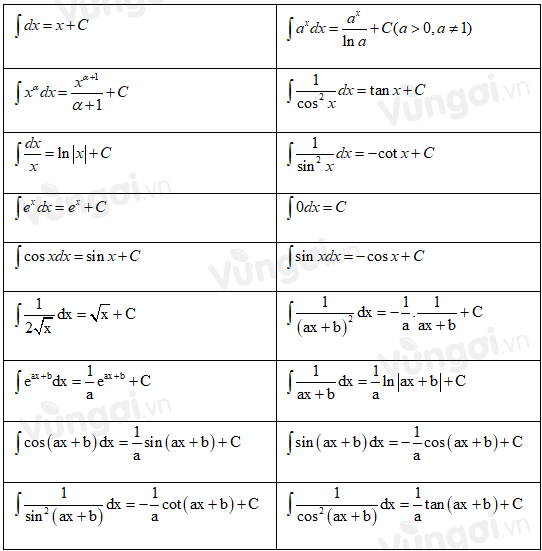
III. Tìm nguyên hàm của hàm số
Phương pháp:
– Bước 1: Biến đổi hàm số \(f\left( x \right)\) về các hàm số sơ cấp có nguyên hàm đã biết.
– Bước 2: Sử dụng định nghĩa, tính chất, bảng nguyên hàm,…để tìm nguyên hàm các hàm số.
Ví dụ: Tìm nguyên hàm của hàm số \(f\left( x \right) = \dfrac{{{{\left( {{x^2} – 1} \right)}^2}}}{{{x^2}}}\).
Giải:
Ta có: \(f\left( x \right) = \dfrac{{{{\left( {{x^2} – 1} \right)}^2}}}{{{x^2}}} = \dfrac{{{x^4} – 2{x^2} + 1}}{{{x^2}}} \) \(= {x^2} – 2 + \dfrac{1}{{{x^2}}}\)
Do đó \(F\left( x \right) = \int {\left( {{x^2} – 2 + \dfrac{1}{{{x^2}}}} \right)dx} \) \(= \int {{x^2}dx} – 2\int {dx} + \int {\dfrac{1}{{{x^2}}}dx} \) \(= \dfrac{{{x^3}}}{3} – 2x – \dfrac{1}{x} + C\).
IV. Tìm hàm số cho biết đạo hàm và giá trị của hàm số tại một điểm
Phương pháp:
– Bước 1: Tìm nguyên hàm của hàm số đã cho, sử dụng định nghĩa, tính chất, bảng nguyên hàm,…
– Bước 2: Thay giá trị đề bài cho vào và tìm hằng số \(C\) suy ra hàm số cần tìm.
Ví dụ: Tìm hàm số \(F\left( x \right)\) biết \(F’\left( x \right) = \dfrac{{x – 1}}{{\sqrt[3]{x}}}\) trên \(\left( {0; + \infty } \right)\) và \(F\left( 1 \right) = 3\).
Giải:
Ta có:
\(\begin{array}{l}F’\left( x \right) = \dfrac{{x – 1}}{{\sqrt[3]{x}}} = \left( {x – 1} \right){x^{ – \frac{1}{3}}} = {x^{\frac{2}{3}}} – {x^{ – \frac{1}{3}}}\\ \Rightarrow F\left( x \right) = \int {F’\left( x \right)dx} = \int {\left( {{x^{\frac{2}{3}}} – {x^{ – \frac{1}{3}}}} \right)dx} \end{array}\)
$ = \dfrac{{{x^{\frac{2}{3} + 1}}}}{{\dfrac{2}{3} + 1}} – \dfrac{{{x^{ – \frac{1}{3} + 1}}}}{{ – \dfrac{1}{3} + 1}} + C = \dfrac{3}{5}{x^{\frac{5}{3}}} – \dfrac{3}{2}{x^{\frac{2}{3}}} + C$
Lại có \(F\left( 1 \right) = 3\) nên \(\dfrac{3}{5}{.1^{\frac{5}{3}}} – \dfrac{3}{2}{.1^{\frac{2}{3}}} + C = 3 \Leftrightarrow C = \dfrac{{39}}{{10}}\).
Vậy \(F\left( x \right) = \dfrac{3}{5}{x^{\frac{5}{3}}} – \dfrac{3}{2}{x^{\frac{2}{3}}} + \dfrac{{39}}{{10}}\).
