I. Tìm hàm số có đồ thị cho trước
Phương pháp:
– Bước 1: Nhận dạng đồ thị: Đồ thị thuộc dạng bậc 3 hay bậc 4, hệ số \(a\) dương hay âm.
– Bước 2: Tìm điểm giao của đồ thị hàm số với \(Oy\) và thay tọa độ vào các hàm số ở từng đáp án.
– Bước 3: Tìm các điểm cực đại, cực tiểu của đồ thị hàm số đã cho.
– Bước 4: Tính đạo hàm các hàm số ở mỗi đáp án và giải phương trình \(y’ = 0\), tìm điểm cực đại, cực tiểu của đồ thị hàm số ở các đáp án.
– Bước 5: Giải phương trình \(y = 0\) ở các đáp án và tìm nghiệm, đối chiếu với hoành độ giao điểm của đồ thị hàm số đã cho với trục hoành.
Ví dụ 1:
Đường cong trong hình vẽ bên là đồ thị của hàm số nào?
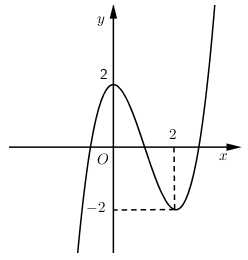
\(y = – {x^3} + x + 2\) B. \(y = {x^3} – 3{x^2} + 2\)
\(y = {x^4} – {x^2} + 1\) D. \(y = {x^3} – 3x + 2\)
Cách giải:
Nhận xét: Đường cong trong hình vẽ là đồ thị của hàm số bậc 3 có hệ số a > 0
Loại đáp án A, C
Xét 2 đáp án B và D
Thay \(x = 0;\,y = 2\) thì cả 2 đáp án B, D đều thỏa mãn
Thay \(x = 2;\,y = – 2\) chỉ có đáp án B thỏa mãn
Chọn B
HS chỉ cần thực hiện từng bước rồi loại bớt đáp án, đến khi chọn được đáp án đúng thì dừng lại, không nhất thiết phải thực hiện hết cả 5 bước nếu đã tìm ra đáp án trước đó để tránh mất thời gian.
II. Tìm hàm số có bảng biến thiên cho trước
Phương pháp:
– Bước 1: Nhận dạng bảng biến thiên: Bảng biến thiên đã cho là của hàm bậc 3 hay bậc 4, hệ số \(a\) âm hay dương.
– Bước 2: Tìm các điểm cực đại, cực tiểu của đồ thị hàm số dựa vào bảng biến thiên.
– Bước 3: Tính đạo hàm các hàm số ở mỗi đáp án và giải phương trình \(y’ = 0\), tìm điểm cực đại, cực tiểu của đồ thị hàm số ở các đáp án.
Ví dụ 2:
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên R có bảng biến thiên:
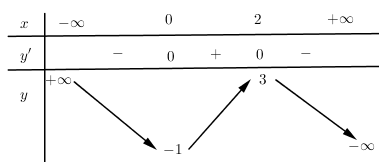
Bảng biến thiên trên là bảng biến thiên của hàm số nào?
- \(y = {x^3} + 2{x^2} – 5\)
- \(y = {x^4} + 2{x^2} – 3\)
- \(y = – {x^3} + 3{x^2} – 1\)
- \(y = – {x^3} – 3{x^2} – 1\)
Cách giải:
Nhận xét: Dễ thấy bảng biến thiên của đồ thị hàm số bậc 3 Þ Loại đáp án B
Ngoài cùng bên phải của \(y’ < 0 \Rightarrow a < 0\) Þ Loại đáp án A
Thay lần lượt hai điểm \(\left( {0;\, – 1} \right)\) và \(\left( {2;\,3} \right)\) vào 2 hàm số còn lại
Thay \(x = 0\) vào cả hai hàm số \(y = – {x^3} + 3{x^2} – 1\) và \(y = – {x^3} – 3{x^2} – 1\) ta thu được \(y = – 1\)
\( \Rightarrow \left( {0;\, – 1} \right)\) đều thuộc vào 2 đồ thị hàm số \(y = – {x^3} + 3{x^2} – 1\) và \(y = – {x^3} – 3{x^2} – 1\)
Thay \(x = 2\) vào hàm số \(y = – {x^3} + 3{x^2} – 1\) ta được y = 3
\( \Rightarrow \left( {2;\,3} \right)\) thuộc vào đồ thị hàm số \(y = – {x^3} + 3{x^2} – 1\)
Thay \(x = 2\) vào hàm số \(y = – {x^3} – 3{x^2} – 1\) ta được \(y = – 21\)
\( \Rightarrow \left( {2;\,3} \right)\) không thuộc vào đồ thị hàm số \(y = – {x^3} – 3{x^2} – 1\)
Chọn C
III. Nhận xét các tính chất của hàm số, đồ thị hàm số có bảng biến thiên cho trước (về tính đơn điệu, cực trị, tâm đối xứng, trục đối xứng,…)
Phương pháp:
– Bước 1: Quan sát bảng biến thiên, tìm các khoảng đơn điệu, các điểm cực trị của hàm số.
– Bước 2: Nhận dạng bảng biến thiên: Bảng biến thiên đã cho là của hàm bậc 3 hay bậc 4, từ đó tìm được tâm đối xứng, trục đối xứng,…
– Bước 3: Đối chiếu các kết quả thu được ở trên với các đáp án bài cho và xét tính đúng sai của các đáp án.
Ví dụ 3:
Cho hàm số \(y = f\left( x \right)\) xác định liên tục trên R có bảng biến thiên:
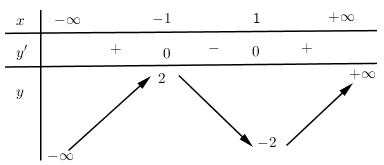
Khẳng định nào sau đây là đúng?
A. Hàm số có giá trị lớn nhất bằng 2
B. Điểm cực đại của đồ thị hàm số là \(x = – 1\)
C. Cực tiểu của hàm số là \(y = – 2\)
D. Điểm cực đại của đồ thị hàm số là \(\left( {1;\, – 2} \right)\)
Cách giải:
Từ bảng biến thiên ta thấy:
– Hàm số không có GTLN nên A sai.
– Điểm cực đại của đồ thị hàm số là \(\left( { – 1;2} \right)\) nên D sai, \(x = – 1\) là điểm cực đại của hàm số nên B sai.
– Giá trị cực tiểu của hàm số là \(y = – 2\) nên C đúng.
Chọn C
HS cũng có thể xét tính đúng sai của từng đáp án ngay mà không cần nhận xét tất cả các tính chất của hàm số, đồ thị hàm số đã nêu ở trên để tránh mất nhiều thời gian.
IV. Tìm điều kiện của các hệ số của hàm đa thức bậc ba có đồ thị cho trước
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\left( {a \ne 0} \right)\) có đồ thị \(\left( C \right)\) cho trước. Tìm điều kiện của \(a,b,c,d\).
Phương pháp:
– Bước 1: Xét tính dương, âm của hệ số \(a\) dựa và dáng đồ thị.
– Bước 2: Tìm điều kiện của \(d\) dựa và giao điểm của đồ thị hàm số với trục \(Oy\).
+ Nếu giao điểm nằm trên trục hoành thì \(d > 0\).
+ Nếu giao điểm nằm dưới trục hoành thì \(d < 0\).
+ Nếu giao điểm trùng với gốc tọa độ \(O\) thì \(d = 0\).
– Bước 3: Tìm điều kiện của \(b,c\) dựa vào các điểm cực trị của đồ thị hàm số:
+ Nếu đồ thị hàm số không có cực trị thì phương trình \(y’ = 0\) vô nghiệm hoặc có nghiệm kép \( \Leftrightarrow \Delta ‘ = {b^2} – 3ac \le 0\).
+ Nếu đồ thị hàm số có hai cực trị thì phương trình \(y’ = 0\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta ‘ = {b^2} – 3ac > 0\).
+ Nếu đồ thị hàm số có hai cực trị nằm trái phía với trục tung thì phương trình \(y’ = 0\) có hai nghiệm phân biệt trái dấu \( \Leftrightarrow 3ac < 0 \Leftrightarrow ac < 0\).
+ Nếu đồ thị hàm số có hai cực trị cùng nằm bên trái trục tung thì phương trình \(y’ = 0\) có hai nghiệm phân biệt cùng âm \( \Leftrightarrow \left\{ \begin{array}{l}\Delta ‘ = {b^2} – 3ac > 0\\S = – \dfrac{{2b}}{{3a}} < 0\\P = \dfrac{c}{{3a}} > 0\end{array} \right.\)
+ Nếu đồ thị hàm số có hai cực trị cùng nằm bên phải trục tung thì phương trình \(y’ = 0\) có hai nghiệm phân biệt cùng dương \( \Leftrightarrow \left\{ \begin{array}{l}\Delta ‘ = {b^2} – 3ac > 0\\S = – \dfrac{{2b}}{{3a}} > 0\\P = \dfrac{c}{{3a}} > 0\end{array} \right.\)
Ví dụ 4:
Cho hàm số\(y = a{x^3} + b{x^2} + cx + d\,\left( {a \ne 0} \right)\)có đồ thị hàm số như hình vẽ dưới đây. Khẳng định nào sau đây về dấu của\(a,b,c,d\)là đúng nhất?
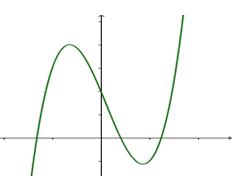
- \(a,d > 0\) B. \(a > 0,c > 0 > b\)
- \(a,b,c,d > 0\) D.\(a,d > 0,c < 0\)
Cách giải
\(\mathop {\lim }\limits_{x \to – \infty } x = – \infty \) nên \(a > 0\)
Dựa vào đồ thị hàm số ta có\(y’ = 3a{x^2} + 2bx + c = 0\) có hai nghiệm phân biệt trái dấu
\( \Rightarrow ac < 0\)mà \(a > 0\)nên suy ra \(c < 0\)suy ra loại B, C.
Mặt khác thấy đồ thị cắt trục oy tại điểm có tung độ dương \( \Rightarrow d > 0\)
Chọn D
V. Tìm điều kiện của tham số để đồ thị hàm số có điểm uốn thỏa mãn điều kiện cho trước
Phương pháp:
– Bước 1: Tính \(y’;y”\), giải phương trình \(y” = 0\).
– Bước 2: Giả sử \({x_0}\) là một nghiệm của phương trình \(y” = 0\) thì điểm uốn \(U\left( {{x_0};f\left( {{x_0}} \right)} \right)\).
– Bước 3: Thay tọa độ điểm uốn vào điều kiện đề bài để tìm \(m\)
