20 Bài tập Một số bài toán về tỉ số và tỉ số phần trăm lớp 6 (sách mới) có đáp án

Bài tập Toán 6 Một số bài toán về tỉ số và tỉ số phần trăm

A. Bài tập Một số bài toán về tỉ số và tỉ số phần trăm

Bài 1: Một cửa hàng dự định bán 15 tấn gạo nhưng trên thực tế cửa hàng đã bán được 12 tấn gạo. Hỏi của hàng đã thực hiện được bao nhiêu phần trăm kế hoạch.

Lời giải:

Cửa hàng đã thực hiện được số phần trăm kế hoạch là:

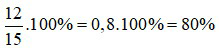
Vậy cửa hàng đã thực hiện được 80

Bài 2: Khối lớp 6 của một trường Trung học cơ sở có 150 học sinh, trong đó có 78 học sinh nữ.

a) Tính tỉ số phần trăm của số học sinh nữ với số học sinh khối 6.

b) Tính số phần trăm của số học sinh nam với số học sinh nữ.

Lời giải:

a) Tỉ số phần trăm của học sinh nữ so với học sinh khối 6 là:

Vậy tỉ số phần trăm của học sinh nữ so với học sinh khối 6 là 52

b) Số học sinh nam của khối 6 là: 

150 – 78 = 72 (học sinh)

Tỉ số phần trăm của số học sinh nam với số học sinh nữ là: 

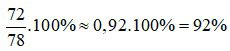
Vậy tỉ số phần trăm của số học sinh nam với số học sinh nữ là 92

Bài 3: Một nhà thầu xây dựng nhận xây một ngôi nhà với chi phí là 360 000 000 đồng nhưng chủ nhà xin giảm đi 2, 5

Lời giải:

Số tiền chủ nhà xin giảm với chủ nhà thầu là:

360 000 000 .   = 9 000 000 (đồng)

Số tiền nhà thầu nhận xây nhà là: 

360 000 000 – 9 000 000 = 351 000 000 (đồng)

Vậy số tiền nhà thầu nhận xây nhà là 351 000 000 đồng.

Bài 4: Một lớp có 25

Lời giải:

Tỉ số phần trăm ứng với 5 học sinh trung bình là: 

100

Số học sinh cả lớp là: 

5 : 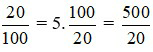  = 25 (học sinh)

Bài 5. Lớp 6A có 36 học sinh, trong đó có 20 học sinh nữ. Tính tỉ số giữa học sinh nam so với số học sinh cả lớp.

Lời giải:

Số học sinh nam của lớp 6A là:

36 −20 = 16 (học sinh).

Tỉ số giữa học sinh nam so với số học sinh cả lớp là:

Vậy tỉ số giữa học sinh nam so với số học sinh cả lớp là .

Bài 6. Viết các số thập phân sau đây dưới dạng tỉ số phần trăm:

−0,56; 7,5; −3,25.

Lời giải:

Các số thập phân được viết dưới dạng tỉ số phần trăm như sau:

−0,56 = −0,56 . 100

7,5 = 7,5 . 100

−3,25 = −12,25 . 100

Bài 7. Viết các phân số sau dưới dạng tỉ số phần trăm:

Lời giải:

Để viết các phân số dưới dạng tỉ số phần trăm, ta làm như sau:

Bước 1: Viết các phân số dưới dạng phân số có mẫu là 100.

Bước 2: Thêm kí hiệu

Các phân số được viết dưới dạng tỉ số phần trăm là:

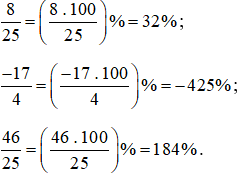
Bài 8. Tính tỉ số của:

a) 2 giờ và 6 giờ;

b) 0,2 tạ và 12 kg;

c) $\frac{3}{5}$ m và 70 cm.

Hướng dẫn giải

a) Tỉ số của 2 giờ và 6 giờ là:

2 : 6 = $\frac{2}{6}=\frac{1}{3}$.

Vậy tỉ số của 2 giờ và 6 giờ là $\frac{1}{3}.$

b) Đổi 0,2 tạ = 20 kg.

Tỉ số của 20 kg và 12 kg là:

20 : 12 = $\frac{20}{12}=\frac{5}{3}$.

Vậy tỉ số của 0,2 tạ và 12 kg là $\frac{5}{3}.$ 

c) Đổi $\frac{3}{5}$ m = 0,6 m = 60 cm.

Tỉ số của 60 cm và 70 cm là:

60 : 70 = $\frac{60}{70}=\frac{6}{7}.$ 

Vậy tỉ số của $\frac{3}{5}$ m và 70 cm là $\frac{6}{7}.$

Bài 9. Tính tỉ số phần trăm (làm tròn kết quả đến hàng phần trăm) của:

a) 0,12 m² và 420 cm²;

b) $\frac{2}{3}$ giờ và 12 phút.

Hướng dẫn giải

a) Đổi 0,12 m² = 12 cm²

Tỉ số phần trăm của 12 cm² và 420 cm² là: $\frac{12}{420}.100\%=\frac{12.100}{420}\%=2,\mathrm{857142\dots }\%$

Làm tròn kết quả đến hàng phần mười: do hàng phần trăm của kết quả là 5 = 5 nên ta có 2,857142…≈ 2,9.

Vậy tỉ số phần trăm của 0,12 m² và 420 cm² là khoảng 2,9

b) Đổi $\frac{2}{3}$ giờ = 40 phút.

Tỉ số phần trăm 40 phút và 12 phút là: $\frac{40}{12}.100\%=\frac{40.100}{12}\%=333,\mathrm{3333..}\%$

Làm tròn kết quả đến hàng phần mười: do hàng phần trăm của kết quả là 3 < 5 nên ta có 333,33333…≈ 333,3.

Vậy tỉ số phần trăm của $\frac{2}{3}$ giờ và 12 phút là 333,3

Bài 10. Minh điều tra về loại quả ưa thích của một số bạn học sinh trong lớp, mỗi bạn trả lời một lần, được kết quả như bảng thống kê sau:

a) Có bao nhiêu bạn tham gia trả lời?

b) Minh đưa ra kết luận rằng tỉ số phần trăm của số bạn thích cam và xoài so với tổng số bạn lớn hơn 50

Hướng dẫn giải

a) Tổng số bạn tham gia trả lời là: 6 + 4 + 3 + 5 + 7 = 25 (bạn)

Vậy có 25 bạn tham gia trả lời.

b) Số bạn thích quả cam và xoài là: 6 + 7 = 13 (bạn)

Tỉ số phần trăm của số bạn thích cam và xoài so với tổng số bạn tham gia trả lời là:

$\frac{13}{25}.100\%=\frac{13.100}{25}\%=52\%$.

Do đó tỉ số phần trăm của số bạn thích cam và xoài so với tổng số bạn lớn hơn 50

Vậy Minh đã kết luận đúng.

Bài 11. 50

Lời giải:

Mảnh vải đó dài là:

Vậy mảnh vải đó dài 25,5 m.

Bài 12. Trên đĩa có 48 quả táo. An ăn hết 25

Lời giải:

Số quả táo An ăn hết là:

48 . 25

Số quả táo còn lại sau khi An ăn hết 25

48 – 12 = 36 (quả táo)

Số quả táo Bình ăn hết là:

 (quả táo)

Số quả táo còn lại trên đĩa là:

36 – 16 = 20 (quả táo)

Vậy trên đĩa còn lại 20 quả táo.

Bài 13. Bác Nga gửi 600 triệu đồng vào ngân hàng theo hình thức không kì hạn với lãi suất 0,65

Lời giải:

Cách tính tiền lãi không có kì hạn là: 

Tính số tiền lãi = Số tiền gửi . lãi suất (

Số tiền lãi bác Nga nhận được sau 120 ngày là:

 (triệu đồng).

Sau 120 ngày, khi rút ra bác Nga nhận được số tiền cả vốn lẫn lãi là:

800 + 1,3 = 801,3 (triệu đồng) = 801 300 000 (đồng).

Vậy sau 120 ngày, khi rút ra bác Nga nhận được số tiền 801 300 000 đồng cả vốn lẫn lãi.

Câu 14. Tỉ số giữa học sinh nam và học sinh nữ là 80

A. 20 học sinh.

B. 17 học sinh.

C. 19 học sinh.

D. 16 học sinh.

Hướng dẫn giải

Trả lời:

Đổi $80\%=\frac{4}{5}$, tức là số học sinh nam bằng $\frac{4}{5}$ số học sinh nữ.

Tổng số phần là:  4 + 5 = 9 (phần)

Lớp 6A có số học sinh nam là: 

36 : 9.4 = 16 (học sinh)

Vậy lớp có 16 học sinh nam.

Đáp án cần chọn là: D

Câu 15. Hiệu của hai số là 21. Biết 37,5

A. 56; 35

B. 45; 56                     

C. 60; 39

D. 56; 45

Hướng dẫn giải

Trả lời:

Đổi $\mathrm{37,5}\%=\frac{3}{8};\mathrm{0,6}=\frac{3}{5}$

Tỉ số giữa số lớn và số nhỏ là: $\frac{3}{5}:\frac{3}{8}=\frac{8}{5}$

Hiệu số phần bằng nhau là: 

8 – 5 = 3 (phần)

Số lớn là: 21:3 × 8 = 56

Số nhỏ là: 56 – 21 = 35

Vậy hai số đó là 56; 35

Đáp án cần chọn là: 

Câu 16. Sắp xếp theo thứ tự tăng dần $23\%;\frac{12}{100};-1\frac{1}{12};-\frac{31}{24};5\frac{1}{2}$ ta được:

A.$-\frac{31}{24}<-1\frac{1}{12}<\frac{12}{100}<5\frac{1}{2}<23\%$

B.$-\frac{31}{24}<-1\frac{1}{12}<23\%<\frac{12}{100}<5\frac{1}{2}$

C.$-\frac{31}{24}<-1\frac{1}{12}<\frac{12}{100}<23\%<5\frac{1}{2}$

D.$-1\frac{1}{12}<-\frac{31}{24}<\frac{12}{100}<23\%<5\frac{1}{2}$

Hướng dẫn giải

Trả lời:

Ta có:$23\%=\frac{23}{100};-1\frac{1}{12}=-\frac{13}{12};5\frac{1}{2}=\frac{11}{2}$

Ta chia thành hai nhóm phân số là: $\frac{23}{100};\frac{12}{100};\frac{11}{2}$ và $-\frac{13}{12};-\frac{31}{24}$

Nhóm 1: $\frac{12}{100}<\frac{23}{100}<1<\frac{11}{2}$ nên $\frac{12}{100}<\frac{23}{100}<\frac{11}{2}$

Nhóm 2: $-\frac{13}{12};-\frac{31}{24}$

$-\frac{13}{12}=\frac{-26}{24}>\frac{-31}{24}$ nên $-\frac{13}{12}>-\frac{31}{24}$

Vậy $-\frac{31}{24}<-\frac{13}{12}<\frac{12}{100}<\frac{23}{100}<\frac{11}{2}$ hay $-\frac{31}{24}<-1\frac{1}{12}<\frac{12}{100}<23\%<5\frac{1}{2}$

Đáp án cần chọn là: C

Câu 17. Tìm x biết $\frac{\left(\mathrm{1,16}-x\right)\mathrm{.5,25}}{\left(10\frac{5}{9}-7\frac{1}{4}\right).2\frac{2}{17}}=75\%$

A. 0

B. $\frac{6}{5}$

C. $\frac{4}{25}$

D. 1

Hướng dẫn giải

Trả lời:

$\frac{\left(\mathrm{1,16}-x\right)\mathrm{.5,25}}{\left(10\frac{5}{9}-7\frac{1}{4}\right).2\frac{2}{17}}=75\%\frac{\left(\frac{116}{100}-x\right).\frac{525}{100}}{\left(\frac{95}{9}-\frac{29}{4}\right).\frac{36}{17}}=\frac{75}{100}\frac{\left(\frac{29}{25}-x\right).\frac{21}{4}}{\frac{119}{36}.\frac{36}{17}}=\frac{3}{4}\frac{\left(\frac{29}{25}-x\right).\frac{21}{4}}{7}=\frac{3}{4}\left(\frac{29}{25}-x\right).\frac{21}{4}.4=7.3\left(\frac{29}{25}-x\right).21=21\frac{29}{25}-x=21:21\frac{29}{25}-x=1x=\frac{29}{25}-1=\frac{4}{25}$

Đáp án cần chọn là: C

Câu 18. Tìm y biết 2y + 30

A. 1

B. 2

C. −1

D. −2

Hướng dẫn giải

Trả lời:

$2y+30\%y=-\mathrm{2,3}2y+\frac{3}{10}y=-\frac{23}{10}\frac{23}{10}y=-\frac{23}{10}y=-\frac{23}{10}:\frac{23}{10}=–1$

Đáp án cần chọn là: C

Câu 19: Trong các công thức sau, công thức nào đúng?

A. Giá bán = giá vốn – lãi

B. Giá bán = giá vốn + lỗ

C. Giá vốn = giá bán + lãi

D. Giá bán = giá vốn + lãi

Trả lời:

Ta có các công thức :

+) Giá bán = giá vốn + lãi;

+) Giá vốn = giá bán – lãi;

+) Lãi = giá bán – giá vốn;

+) Giá bán = giá vốn – lỗ.

Vậy công thức đúng là:

Giá bán = giá vốn + lãi.

Đáp án cần chọn là: D

Câu 20: Một cửa hàng bán tạp hóa cả ngày bán được 7440000 đồng. Nếu tiền bán được tăng thêm 400000 đồng thì tiền lãi sẽ là 1640000 đồng. Hỏi tiền lãi thực sự bằng bao nhiêu phần trăm tiền vốn?

A. 20

B. 22,04

C. 24,4

D. 28

Trả lời:

Tiền lãi thực sự cửa hàng thu được là:

1640000 – 400000 = 1240000 (đồng)

Tiền vốn là:

7440000 – 1240000 = 6200000 (đồng)

Tỉ số phần trăm của tiền lãi so với tiền vốn là:

1240000 : 6200000 = 0,2 = 20

Đáp số: 20

Đáp án cần chọn là : A

B. Lý thuyết Một số bài toán về tỉ số và tỉ số phần trăm

1. Tỉ số và tỉ số phần trăm

– Tỉ số của số a và số b là thương của phép chia a cho b, được viết là a : b (với b khác 0)

Tỉ số của hai đại lượng (cùng loại và cùng đơn vị đo) là tỉ số hai số đo cùng hai đại lượng đó.

Ví dụ 1: 

Tỉ số của 3 và  là 3 :  

Tỉ số của 1 dm và 1 m là 1 : 10 vì ta phải đổi về cùng đơn vị do đó ta đổi 1 m = 10 dm.

– Trong thực hành, ta thường dùng tỉ số dưới dạng tỉ số phần trăm.

– Tỉ số phần trăm của hai số a và b là  

2. Hai bài toán về tỉ số phần trăm

Bài 1: Tìm giá trị phần trăm của một số cho trước.

Muốn tìm m

Ví dụ 2: 75

Bài 2: Tìm một số biết giá trị phần trăm của số đó: 

Muốn tìm một số khi biết m

Ví dụ 3: 25