Lý thuyết khoảng cách từ điểm đến mặt phẳng tư duy định lượng ĐGNL

I. Định nghĩa khoảng cách từ điểm đến mặt phẳng

– Khoảng cách từ điểm \(M\) đến mặt phẳng \(\left( P \right)\) là khoảng cách giữa hai điểm \(M\) và \(H\), trong đó \(H\) là hình chiếu của điểm \(M\) trên mặt phẳng \(\left( P \right)\).

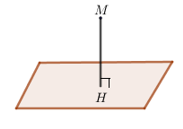
Kí hiệu: \(d\left( {M,\left( P \right)} \right) = MH\).

II. Tính khoảng cách từ một điểm đến một mặt phẳng

Phương pháp:

Để tính được khoảng từ điểm $A$ đến mặt phẳng $\left( \alpha  \right)$ thì điều quan trọng nhất là ta phải xác định được hình chiếu của điểm $A$ trên $\left( \alpha  \right)$.

TH1:

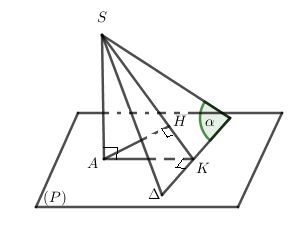
– Dựng \(AK \bot \Delta  \Rightarrow \Delta  \bot \left( {SAK} \right) \Rightarrow \left( \alpha  \right) \bot \left( {SAK} \right)\) và \(\left( \alpha  \right) \cap \left( {SAK} \right) = SK\).

– Dựng \(AH \bot SK \Rightarrow AH \bot \left( \alpha  \right) \Rightarrow d\left( {A,\left( \alpha  \right)} \right) = AH\)

TH2:

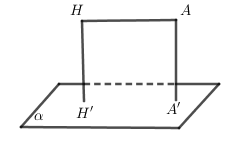
– Tìm điểm \(H \in \left( \alpha  \right)\) sao cho \(AH//\left( \alpha  \right) \Rightarrow d\left( {A,\left( \alpha  \right)} \right) = d\left( {H,\left( \alpha  \right)} \right)\)

TH3:

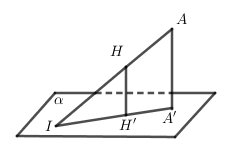
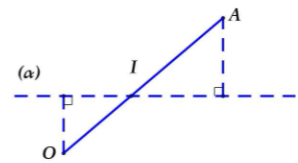
– Tìm điểm \(H\) sao cho \(AH \cap \left( \alpha  \right) = I\)

– Khi đó: \(\dfrac{{d\left( {A,\left( \alpha  \right)} \right)}}{{d\left( {H,\left( \alpha  \right)} \right)}} = \dfrac{{IA}}{{IH}} \Rightarrow {\rm{ }}d\left( {A,\left( \alpha  \right)} \right) = \dfrac{{IA}}{{IH}}.d\left( {H,\left( \alpha  \right)} \right){\rm{ }}\)

Một kết quả có nhiều ứng dụng để tính khoảng cách từ một điểm đến mặt phẳng đối với tứ diện vuông (tương tư như hệ thức lượng trong tam giác vuông) là: