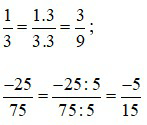Bài tập Toán 6 Mở rộng phân số. Phân số bằng nhau
A. Bài tập Mở rộng phân số. Phân số bằng nhau
Bài 1: Hoàn thành bảng sau:
Phân số | Đọc | Tử số | Mẫu số |
| ? | ? | ? |
| ? | ? | ? |
? | âm sáu phần mười một | ? | ? |
? | ? | 13 | 21 |
Lời giải:
Phân số | Đọc | Tử số | Mẫu số |
| ba phần tư | 3 | 4 |
| một phần âm ba | 1 | –3 |
| âm sáu phần mười một | –6 | 11 |
| mười ba phần hai mươi mốt | 13 | 21 |
Bài 2: Cho các phân số 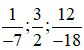 . Với mỗi phân số đã cho hãy tìm một phân số bằng nó sao cho phân số tìm được có mẫu số dương.
. Với mỗi phân số đã cho hãy tìm một phân số bằng nó sao cho phân số tìm được có mẫu số dương.
Lời giải:
+ Ta có:![]()
Vậy phân số tìm được là ![]() .
.
+ Ta có: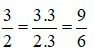
Vậy phân số tìm được là ![]() .
.
+ Ta có: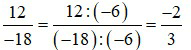
Vậy phân số tìm được là ![]() .
.
Bài 3: Các cặp phân số sau đây có bằng nhau không? Vì sao?
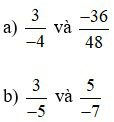
Lời giải:
a) Ta có: 3.48 = 144 và (–4).(–36) = 144
Vì 3.48 = (–4).(–36) = 144 nên![]()
b) Ta có: 3.(–7) = –21 và 5.(–5) = –25
Vì 3.(–7) 5.(–5) (–21 –25) do đó: 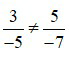 .
.
Câu 4. Viết số nguyên – 16 dưới dạng phân số ta được:
A.
B.
C.
D.
Viết số nguyên – 16 dưới dạng phân số ta được:
Đáp án cần chọn là: C
Câu 5. Nhận xét nào sau đây là đúng khi nói về phân số?
A. Phân số nhỏ hơn số 0 gọi là phân số âm.
B. Phân số lớn hơn số 0 gọi là phân số dương.
C. Phân số âm nhỏ hơn phân số dương.
D. Cả A, B và C đều đúng.
Những nhận xét đúng là:
– Phân số nhỏ hơn số 0 gọi là phân số âm.
– Phân số lớn hơn số 0 gọi là phân số dương.
– Phân số âm nhỏ hơn phân số dương.
Đáp án cần chọn là: D
Câu 6. Phân số có tử bằng −4, mẫu bằng 5 được viết là:
A.
B.
C.
D.
Phân số có tử bằng −4, mẫu bằng 5 được viết là:
Đáp án cần chọn là: C
Câu 7. Tổng các số a; b; c thỏa mãn là:
A. 1161
B. −1125
C. −1053
D. 1089
Ta có:
Vậy
Đáp án cần chọn là: B
Câu 8. Cho tập A = {1;−2; 3; 4}. Có bao nhiêu phân số có tử số và mẫu số thuộc A mà có tử số khác mẫu số và tử số trái dấu với mẫu số?
A. 9
B. 6
C. 3
D. 12
Các phân số thỏa mãn bài toán là:
Vậy có tất cả 6 phân số.
Đáp án cần chọn là: B
Câu 9. Viết phân số âm năm phần tám
A.
B.
C.
D. -5,8
Phân số âm năm phần tám được viết là
Đáp án cần chọn là: C
Câu 10. Trong các cách viết sau đây, cách viết nào cho ta phân số:
A.
B.
C.
D.
+) không là phân số vì mẫu số bằng 0.
+) không là phân số vì mẫu số là số thập phân.
+) không là phân số vì tử số và mẫu số là số thập phân.
+) là phân số vì và mẫu số là 5 khác 0.
Đáp án cần chọn là: B
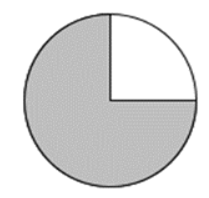
Câu 11. Phần tô màu trong hình sau biểu diễn phân số nào?
A.
B.
C.
D.
Quan sát hình vẽ ta thấy nếu chia hình tròn làm 4 phần thì phần tô màu chiếm 3 phần.
Vậy phân số biểu diễn phần tô màu là
Đáp án cần chọn là: C
Câu 12. Phân số nào dưới đây bằng với phân số
A.
B.
C.
D.
Đáp án A: Vì nên
→ A sai.
Đáp án B: Vì nên
→ B đúng
Đáp án C: Vì nên
→ C sai.
Đáp án D: Vì nên
→ D sai.
Đáp án cần chọn là: B
Câu 13. Điền số thích hợp vào chỗ chấm
A. 20
B. −60
C. 60
D. 30
<=> <=> <=>x = 30
Vậy số cần điền là 30
Đáp án cần chọn là: D
Câu 14. Tính tổng các giá trị biết rằng
A. 22
B. 20
C. 18
D. 15
Ta có:
Vậy tổng các giá trị của x thỏa mãn là: (−2) + (−1) + … + 5 + 6 = 18
Đáp án cần chọn là: C
Câu 15. Tìm tập hợp các số nguyên n để có giá trị là số nguyên.
A.
B.
C.
D.
Ta có:
Vì nên để thì
Ta có bảng:
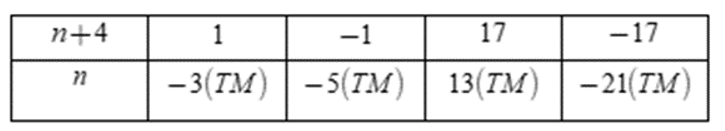
Vậy
Đáp án cần chọn là: B
Câu 16. Có bao nhiêu cặp số nguyên (x; y) thỏa mãn và x > y
A. 4
B. 3
C. 2
D. 1
Ta có:
Mà
Và
Nên
Đáp án cần chọn là: A
Câu 17. Chọn câu sai?
A.
B.
C.
D.
Đáp án A: Vì nên
→ A đúng
Đáp án B: Vì nên
→ B đúng
Đáp án C: Vì nên
→ C sai
Đáp án D: Vì nên
→ D đúng
Đáp án cần chọn là: C
Câu 18. Tìm số nguyên x biết
A. x = 7
B. x = 5
C. x = 15
D. x = 6
Vậy x = 7
Đáp án cần chọn là: A
Câu 19. Viết 20 dm2 dưới dạng phân số với đơn vị là mét vuông
A.
B.
C.
D.
Ta có:
Đáp án cần chọn là: B
Câu 20. Cho biểu thức . Tìm tất cả các giá trị của n nguyên để giá trị của C là một số tự nhiên.
A. n ∈{−6; −1; 0; 5}
B. n ∈{−1; 5}
C. n ∈{0; 5}
D. n ∈{1; 11}
VìC ∈ N nên C ∈ Z. Do đó ta tìm n ∈ Z để C ∈ Z
Vìn ∈ Z nên để C ∈ Z thì 2n + 1 ∈ U(11) = {±1 ;±11}
Ta có bảng:
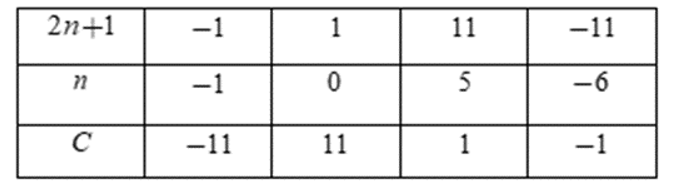
VìC ∈ N nên ta chỉ nhận các giá trị n = 0; n = 5
Đáp án cần chọn là: C
B. Lý thuyết Mở rộng phân số. Phân số bằng nhau
1. Mở rộng khái niệm về phân số
– Định nghĩa về phân số: Với a, b ∈ ℤ, b ≠ 0 , ta gọi ![]() là một phân số, trong đó a là tử số (tử), b là mẫu số (mẫu) của phân số.
là một phân số, trong đó a là tử số (tử), b là mẫu số (mẫu) của phân số.
Ví dụ 1:
![]() là một phân số với tử số là 5 và mẫu số là 4 đọc là năm phần tư.
là một phân số với tử số là 5 và mẫu số là 4 đọc là năm phần tư.
![]() là một phân số với tử số là –10 và mẫu số là 4 đọc là âm mười phần tư.
là một phân số với tử số là –10 và mẫu số là 4 đọc là âm mười phần tư.
![]() là một phân số với tử số là 3 và mẫu số là –7 đọc là ba phần âm bảy.
là một phân số với tử số là 3 và mẫu số là –7 đọc là ba phần âm bảy.
Chú ý: Mọi số nguyên đều có thể viết dưới dạng phân số.
Ví dụ 2:
Số 3 có thể viết dưới dạng phân số là ![]() .
.
Số –8 có thể viết dưới dạng phân số là ![]() .
.
2. Hai phân số bằng nhau
Hai phân số ![]() và
và ![]() được gọi là bằng nhau nếu a.d = b.c. Khi đó ta viết là
được gọi là bằng nhau nếu a.d = b.c. Khi đó ta viết là ![]() .
.
Ví dụ 3: Hai phân số 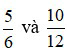 bằng nhau vì 5.12 = 60 và 6.10 = 60.
bằng nhau vì 5.12 = 60 và 6.10 = 60.
3. Tính chất cơ bản của phân số
– Nếu nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.
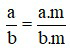 với a, b, m ∈ ℤ; b≠0; m≠0.
với a, b, m ∈ ℤ; b≠0; m≠0.
– Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.
![]() với n là ước chung của a và b; a, b, m ∈ ℤ; b≠0 .
với n là ước chung của a và b; a, b, m ∈ ℤ; b≠0 .
Ví dụ 4: