Giải SGK Toán lớp 10 Bài 12 (Kết nối tri thức): Số gần đúng và sai số

Giải bài tập Toán lớp 10 Bài 12: Số gần đúng và sai số

Giải Toán 10 trang 73 Tập 1 Kết nối tri thức

Câu hỏi mở đầu trang 73 Toán lớp 10: Đỉnh Everest được mệnh danh là “nóc nhà của thế giới”, bởi đây là đỉnh núi cao nhất trên Trái Đất so với mực nước biển. Có rất nhiều con số khác nhau đã từng được công bố về chiều cao của đỉnh Everest: 8 848 m;8 848,13m;8 844.43 m;8 850 m:… Vì sao lại có nhiều kết quả khác nhau như vậy và đâu là con số chính xác?

Lời giải:

Khi đo độ cao đỉnh núi Everest người ta không thể đo trực tiếp một cách chính xác mà phải thông qua tính toán.

Mỗi vị trí quan sát hoặc trong tính toán, có những con số không thể lấy chính xác đo đó kết quả thu được cũng không giống nhau.

Ngoài ra có thể người ta đã làm tròn kết quả để được một con số gọn mà chính xác nhất có thể, nên các kết quả cũng khác nhau.

1. Số gần đúng

Giải Toán 10 trang 74 Tập 1 Kết nối tri thức

HĐ1 trang 74 Toán lớp 10: Ngày 8-12-2020, Trung Quốc và Nepal ra thông cáo chung khẳng định chiều cao mới đo được của đỉnh núi cao nhất thế giới Everest là 8 848,86 m.

(Theo Tuoitre.vn)

Trong các số được đưa ra ở tình huống mở đầu, số nào gần nhất với số được công bố ở trên?

Phương pháp giải:

Lấy 8 848,86 trừ đi các số xuất hiện ở tình huống mở đầu và so sánh các giá trị tuyệt đối của các hiệu vừa tìm được.

Lời giải:

Ta có: $| 8848, 86 - 8848 | = 0, 86$

$| 8848, 86 - 8848, 13 | = 0, 73$

$| 8848, 86 - 8844, 43 | = 4, 43$

$| 8848, 86 - 8850 | = 1, 14$

Trong các số 0,86; 0,73; 4,43; 1,14 thì số 0,73 là số nhỏ nhất.

Do đó trong các số 8 848 m; 8 848,13 m; 8 844,43 m; 8 850 m thì số ; 8 848,13 m là số gần nhất với số được công bố ngày 8-12-2020.

Chú ý

Giá trị tuyệt đối |a-b| càng nhỏ thì a và b càng gần nhau.

HĐ2 trang 74 Toán lớp 10:

Trang và Hoà thực hiện đo thể tích một cốc nước bằng hai ống đồng có vạch chia được kết quả như Hình 5.1.

Hãy cho biết số đo thể tích trên mỗi ống.

Phương pháp giải:

Đọc các số xuất hiện tại vạch nước ở mỗi ống.

Lời giải:

Giả sử ống nước thứ nhất là trang đo và ống nước thứ hai là Hòa đo.

Khi đó ống thứ nhất đo được là 13 $c m^{3}$ , ống thứ hai là 13,1 $c m^{3}$

Chú ý

Với ống thứ hai thì có vạch chia nhỏ hơn.

Câu hỏi trang 74 Toán lớp 10:

Hãy lấy một ví dụ về số gần đúng.

Phương pháp giải:

Số gần đúng là số mà ta khó có thể biết được giá trị chính xác của nó mà chỉ tìm được giá trị xấp xỉ của nó mà thôi.

Lời giải:

Ta không thể biết chính xác giá trị của $\sqrt{3}$ .

Số gần đúng của $\sqrt{3}$ là 1,73.

Chú ý

Ta có thể lấy các số khác như $\sqrt{2}; \sqrt{p}$ với p là số nguyên tố hoặc số $π$ .

Luyện tập 1 trang 74 Toán lớp 10: Gọi P là chu vi của đường tròn bán kính 1cm. Hãy tìm một giá trị gần đúng của P.

Phương pháp giải:

Sử dụng công thức tính chu vi đường tròn $P = 2 π R$ với R là bán kính của đường tròn đó.

Cách bấm máy tính tìm $π$ :

Lời giải:

Chu vi đường tròn là:

$P = 2 π R = 2 π .1 = 2 π (c m)$

Bấm máy tính ta thấy $2 π \approx 6, 28$

Vậy $P \approx 6, 28 c m$ .

Chú ý

Ta có thể lấy số gần đúng khác của $2 π$ như: 6,283 hoặc 6,283185

2. Sai số tuyệt đối và sai số tương đối

HĐ3 trang 74 Toán lớp 10:

Trong HĐ2, Hòa dùng kính lúp để quan sát mực nước trên ống đo thứ hai được hình ảnh như Hình 5.2. Kí hiệu $\bar{a}$ ( $c m^{3}$ ) là số đo thể tích của nước.

Quan sát hình vẽ để so sánh $| 13 - \bar{a} |$ và $| 13, 1 - \bar{a} |$ rồi cho biết trong hai số đo thể tích $13 c m^{3}$ và $13, 1 c m^{3}$ , số đo nào gần với thể tích của cốc nước hơn.

Phương pháp giải:

Quan sát hình vẽ 5.2 và kiểm tra giữa hai số 13,1 và 13, số nào gần $\bar{a}$ hơn.

Lời giải:

Ta quan sát hình trên thì thấy số 13,1 gần $\bar{a}$ hơn.

Giải Toán 10 trang 75 Tập 1 Kết nối tri thức

Luyện tập 2 trang 75 Toán lớp 10: Một phép đo đường kính nhân tế bào cho kết quả là $5 \pm 0, 3 μ m$ . Đường kính thực của nhân tế bào thuộc đoạn nào?

Phương pháp giải:

Ta viết $\bar{a} = a \pm d$ thì có nghĩa là số đúng $\bar{a}$ nằm trong đoạn $[a - d; a + d]$ .

Với a là số gần đúng của $\bar{a}$ và d là độ chính xác của $\bar{a}$ .

Lời giải:

Gọi $\bar{a}$ là đường kính thực của nhân tế bào.

Vì phép đo đường kính nhân tế bào cho kết quả là $5 \pm 0, 3 μ m$ .

=> $a = 5 μ m; d = 0, 3 μ m$

Nên ta có $\bar{a}$ nằm trong đoạn $[5 - 0, 3; 5 + 0, 3]$ hay $[4, 7; 5, 3]$ .

HĐ4 trang 75 Toán lớp 10:

Công ty (trong Ví dụ 2) cũng sử dụng dây chuyền B để đóng gạo với khối lượng chính

xác là 20 kg. Trên bao bì ghi thông tin khối lượng là $20 \pm 0, 5$ kg.

Khẳng định “Dây chuyền A tốt hơn dây chuyền B” là đúng hay sai?

Lời giải:

Mặc dù độ chính xác của khối lượng bao gạo đóng bằng dây chuyền A nhỏ hơn nhưng do bao gạo đóng bằng dây chuyền B nặng hơn nhiều nên ta không dựa vào sai số tuyệt đối để so sánh.

Do đó câu hỏi này ta chưa thể trả lời chính xác được nếu chỉ dựa vào các kiến thức đã học trước đó.

Xem thêm bài Luyện tập 3 trang 76 Sách giáo khoa Toán 10 – Kết nối tri thức với cuộc sống.

Giải Toán 10 trang 76 Tập 1 Kết nối tri thức

Luyện tập 3 trang 76 Toán lớp 10: Đánh giá sai số tương đối của khối lượng bao gạo được đóng gói theo hai dây chuyền A, B ở Ví dụ 2 và HĐ4. Dựa trên tiêu chí này, dây chuyền nào tốt hơn?

Phương pháp giải:

– Đánh giá sai số tương đối: $δ_{a} \leq \frac{d}{| a |}$

Với d là độ chính xác và a là số gần đúng.

– Nhận xét dây chuyền nào tốt hơn: $\frac{d}{| a |}$ càng nhỏ thì chất lượng phép đo hay tính toán càng cao.

Lời giải:

Xét dây chuyền A: ta có d=0,2; a=5.

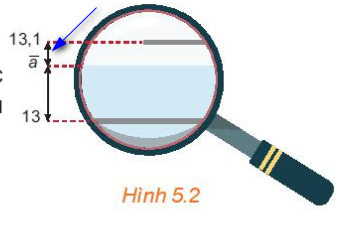
$δ_{5} \leq \frac{0, 2}{| 5 |} = 0, 04 = 4 Xét dây chuyền B: ta có d=0,5; a=20δ_{5} \leq \frac{0, 5}{| 20 |} = 0, 025 = 2, 5 Ta thấy2, 5 Chú ýCó thể không cần đổi sang đơn vị phần trăm (3. Quy tròn số gần đúngGiải Toán 10 trang 77 Tập 1 Kết nối tri thứcLuyện tập 4 trang 77 Toán lớp 10: Hãy viết số quy tròn của số gần đúng trong những trường hợp sau:a)11251900 \pm 300b) 18, 2857 \pm 0, 01Phương pháp giải :Bước 1: Xác định hàng làm tròn.Cho số gần đúng a với độ chính xác d. Khi được yêu cầu làm tròn số a mà không nói rõlàm tròn đến hàng nào thì ta làm tròn số a đến hàng thấp nhất mà ở nhỏ hơn 1 đơn vị của hàng đó.Bước 2: Làm tròn:Đối với chữ số hàng làm tròn:– Giữ nguyên nểu chữ số ngay bên phải nó nhỏ hơn 5;– Tăng 1 đơn vị nếu chữ số ngay bên phải nó lớn hơnhoặc bằng 5.Đối với chữ số sau hàng làm tròn:– Bỏ đi nếu ở phần thập phân;– Thay bởi các chữ số 0 nếu ở phần số nguyên.Lời giải :a)Bước 1:Vì độ chính xác đến hàng trăm (d=300) nên hàng làm tròn là hàng nghìn. Chữ số hàng làm tròn là 1.Bước 2:Vì số bên phải số 1 là số 9>5 nên ta tăng số 1 thêm 1 đơn vị.Vậy số quy tròn của 11251900 là 11252000b)Vì độ chính xác đến hàng phần trăm (d=0,01) nên hàng làm tròn là hàng phần chục. Chữ số hàng làm tròn là 2.Vì số bên phải số 2 là số 8>5 nên ta tăng 2 thêm 1 đơn vị và bỏ các số sau số 2.Vậy số quy tròn của 18, 2857 là 18, 3 .Vận dụng trang 77 Toán lớp 10 : Các nhà vật lí sử dụng hai phương pháp khác nhau để đo tuổi của vũ trụ (đơn vị tỉ năm) lần lượt cho hai kết quả là: 13,807 \pm 0,026 và 13,799 \pm 0,021.Hãy đánh giá sai số tương đối của mối phương pháp. Căn cứ trên tiêu chí này, phương pháp nào cho kết quả chính xác hơn?Phương pháp giải :– Đánh giá sai số tương đối: δ_{a} \leq \frac{d}{| a |}Với d là độ chính xác và a là số gần đúng.– Nhận xét phương pháp nào cho kết quả chính xác hơn: \frac{d}{| a |} càng nhỏ thì chất lượng phép đo hay tính toán càng cao.Lời giải :Xét phương pháp 1: ta có d=0,026(tỉ năm); a=13,807 (tỉ năm)δ_{5} \leq \frac{0, 026}{| 13, 807 |} \approx 1, {88.10}^{- 3} = 0, 00188Xét phương pháp 2: ta có d=0,021(tỉ năm); a=13,799 (tỉ năm)δ_{5} \leq \frac{0, 021}{| 13, 799 |} \approx 1, {52.10}^{- 3} = 0, 00152Ta thấy 0, 00188 > 0, 00152 nên phương pháp 2 cho kết quả chính xác hơn.Bài tậpBài 5.1 trang 77 Toán lớp 10 : Trong các số sau, những số nào là số gần đúng?a) Cân một túi gạo cho kết quả là 10,2kgb) Bán kính Trái Đất là 6 371 km.c) Trái Đất quay một vòng quanh Mặt Trời mất 365 ngày.Phương pháp giải :Các con số thu thập được nhờ đo đạc đều là các số gần đúng.Lời giải :a) Khi cân một túi gạo thì ta kết quả là một số gần đúng vì đây là một cách đo đạc.b) Ta không biết chính xác bán kính Trái Đất nên 6 371 cũng là số gần đúng.c) Trái Đất quay một vòng quanh Mặt Trời mất 365 ngày cũng là số gần đúng.Bài 5.2 trang 77 Toán lớp 10 : Giải thích kết quả “Đo độ cao của một ngọn núi cho kết quả là 1 235 +5 m” và thực hiện làm tròn số gần đúng.Phương pháp giải :– Giải thích: Chỉ ra số độ cao gần đúng và độ chính xác– Làm tròn số gần đúng:Bước 1: Xác định hàng làm tròn.Cho số gần đúng a với độ chính xác d. Khi được yêu cầu làm tròn số a mà không nói rõlàm tròn đến hàng nào thì ta làm tròn số a đến hàng thấp nhất mà ở nhỏ hơn 1 đơn vị của hàng đó.Bước 2: Làm tròn:Đối với chữ số hàng làm tròn:– Giữ nguyên nểu chữ số ngay bên phải nó nhỏ hơn 5;– Tăng 1 đơn vị nếu chữ số ngay bên phải nó lớn hơnhoặc bằng 5.Đối với chữ số sau hàng làm tròn:– Bỏ đi nếu ở phần thập phân;– Thay bởi các chữ số 0 nếu ở phần số nguyên.Lời giải :– Giải thích: “Đo độ cao của một ngọn núi cho kết quả là 1 235 \pm 5 m” có nghĩa làĐộ cao của ngọn núi gần với 1235m và độ chính xác là 5mBài 5.3 trang 77 Toán lớp 10 : Sử dụng máy tính cầm tay tìm số gần đúng cho \sqrt[3]{7} với độ chính xác 0.0005.Phương pháp giải :Làm tròn số gần đúng:Bước 1: Xác định hàng làm tròn.Cho số gần đúng a với độ chính xác d. Khi được yêu cầu làm tròn số a mà không nói rõ làm tròn đến hàng nào thì ta làm tròn số a đến hàng thấp nhất mà ở nhỏ hơn 1 đơn vị của hàng đó.Bước 2: Làm tròn:Đối với chữ số hàng làm tròn:– Giữ nguyên nểu chữ số ngay bên phải nó nhỏ hơn 5;– Tăng 1 đơn vị nếu chữ số ngay bên phải nó lớn hơnhoặc bằng 5.Đối với chữ số sau hàng làm tròn:– Bỏ đi nếu ở phần thập phân;– Thay bởi các chữ số 0 nếu ở phần số nguyên.Lời giải :Ta đượcTa chọn số gần đúng là 1,912931183.Độ chính xác d=0.0005 nên ta có hàng làm tròn là hàng phần nghìn.Số ở hàng phần nghìn là số 2, số bên phải là số 9>5 nên ta tăng 2 thêm 1 đơn vị và được số quy tròn của 1,912931183 là 1,913Bài 5.4 trang 77 Toán lớp 10 : Các nhà vật lí sử dụng ba phương pháp đo hằng số Hubble lần lượt cho kết quả như sau:67,31 \pm 0,96;67,90 \pm 0,55;67,74 \pm 0,46.Phương pháp nào chính xác nhất tính theo sai số tương đối?Phương pháp giải :Đánh giá sai số tương đối của 3 phương pháp.– Đánh giá sai số tương đối: δ_{a} \leq \frac{d}{| a |}Với d là độ chính xác và a là số gần đúng.– Nhận xét phương pháp nào cho kết quả chính xác hơn: \frac{d}{| a |} càng nhỏ thì chất lượng phép đo hay tính toán càng cao.Lời giải :Phương pháp 1: 67,31 \pm 0,96a = 67, 31; d = 0, 96Sai số tương đối δ_{1} \leq \frac{d}{| a |} = \frac{0, 96}{67, 31} \approx 0, 014Phương pháp 2: 67,90 \pm 0,55a = 67, 90; d = 0, 55Sai số tương đối δ_{2} \leq \frac{d}{| a |} = \frac{0, 55}{67, 90} \approx 8, {1.10}^{- 3} = 0, 0081Phương pháp 1: 67,74 \pm 0,46a = 67, 74; d = 0, 46Sai số tương đối δ_{3} \leq \frac{d}{| a |} = \frac{0, 46}{67, 74} \approx 6, {8.10}^{- 3} = 0, 0068Ta thấy 0, 14 > 0, 0081 > 0, 0068=> phương pháp 3 có chính xác nhất.Bài 5.5 trang 77 Toán lớp 10 : An và Bình cùng tính chu vi của hình tròn bán kính 2 cm với hai kết quả như sau:Kết quả của An: S_{1} = 2 π R \approx 2.3, 14.2 = 12, 56 cm;Kết quả của Bình: S_{2} = 2 π R \approx 2.3, 1.2 = 12, 4 cm.Hỏi:a) Hai giá trị tính được có phải là các số gần đúng không?b) Giá trị nào chính xác hơn?Phương pháp giải :a) Chu vi của đường tròn luôn là số gần đúng.b) Đánh giá sai số tuyệt đốiLời giải :a) Vì công thức chu vi đường tròn là 2 π R với R là độ dài bán kính, trong đó π là số không thể tính chính xác được mà chỉ có thể lấy số gần đúng nên hai giá trị tính được là số gần đúng.b)Kết quả của An: S_{1} = 2 π R \approx 2.3, 14.2 = 12, 56 cm:Kết quả của Bình: S_{2} = 2 π R \approx 2.3, 1.2 = 12, 4 cm.Ta thấy 3, 14 < 3, 1 => S_{1} < S_{2}=> | 2 π R - S_{1} | > | 2 π R - S_{2} |=> Kết quả của An chính xác hơn.Bài 5.6 trang 77 Toán lớp 10 : Làm tròn số 8 316,4 đến hàng chục và 9,754 đến hàng phần trăm rồi tính sai số tuyệt đối của số quy tròn.Phương pháp giải :* Làm tròn số gần đúng:Bước 1: Xác định hàng làm tròn.Cho số gần đúng a với độ chính xác d. Khi được yêu cầu làm tròn số a mà không nói rõ làm tròn đến hàng nào thì ta làm tròn số a đến hàng thấp nhất mà ở nhỏ hơn 1 đơn vị của hàng đó.Bước 2: Làm tròn:Đối với chữ số hàng làm tròn:– Giữ nguyên nểu chữ số ngay bên phải nó nhỏ hơn 5;– Tăng 1 đơn vị nếu chữ số ngay bên phải nó lớn hơnhoặc bằng 5.Đối với chữ số sau hàng làm tròn:– Bỏ đi nếu ở phần thập phân;– Thay bởi các chữ số 0 nếu ở phần số nguyên.* Tính sai số tuyệt đối của số quy tròn.Lời giải :– Làm tròn số 8 316,4 đến hàng chụcSố làm tròn là số 1, số bên phải số 1 là số 6>5=> Tăng thêm 1 đơn vị=> Số quy tròn là: 8 320Sai số tuyệt đối: | 8320 - 8316, 4 | = 3, 6– Làm tròn số 9,754 đến hàng phần trămSố làm tròn là số 5, số bên phải số 5 là số 4<5=> Giữ nguyên 5 và bỏ các số bên phải đi.=> Số quy tròn là: 9,75Sai số tuyệt đối: | 9, 754 - 9, 75 | = 0, 004Lý thuyết Số gần đúng và sai số1. Số gần đúngTrong nhiều trường hợp, ta không biết hoặc khó biết số đúng (kí hiệu là \bar{a}) mà chỉ tìm được giá trị xấp xỉ nó. Giá trị này được gọi là số gần đúng, kí hiệu là a.Chú ý:Ta có thể sử dụng máy tính cầm tay để tìm giá trị gần đúng của các biểu thức chứa các số vô tỉ như π, \sqrt{a}, \sqrt[3]{a},…Ví dụ:+ Hình tròn có bán kính R = 2cm.Chu vi của hình tròn là 2.π.2 = 4π ≈ 12,57 (cm).Vậy 4π là số đúng; 12,57 là số gần đúng của chu vi hình tròn.+ Ta có \sqrt[3]{3} \approx 1,44 .Vậy \sqrt[3]{3} là số đúng; 1,44 là số gần đúng.2. Sai số tuyệt đối và sai số tương đốia) Sai số tuyệt đốiGiá trị Δ_{a} = (a - \bar{a}) phản ánh mức độ sai lệch giữa số đúng \bar{a} và số gần đúng a, được gọi là sai số tuyệt đối của số gần đúng a.Ví dụ:Ta có: 3^{7} . \sqrt{6} \approx 5357 .Suy ra \bar{a} = 3^{7} . \sqrt{6} là số đúng; a = 5357 là số gần đúng.Khi đó ta có: Δ_{a} = (a - \bar{a}) = (5357 - 3^{7} . \sqrt{6}) \approx 0,034 .Vậy ∆ a = 0,034 là sai số tuyệt đối của số gần đúng a = 5357.Chú ý:+ Trên thực tế, nhiều khi ta không biết \bar{a} nên cũng không biết ∆ a . Tuy nhiên, ta có thể đánh giá được ∆ a không vượt quá một số dương d nào đó.+ Nếu ∆ a ≤ d thì a – d ≤ \bar{a} ≤ a + d, khi đó ta viết \bar{a} = a ± d và hiểu là số đúng \bar{a} nằm trong đoạn [a – d; a + d]. 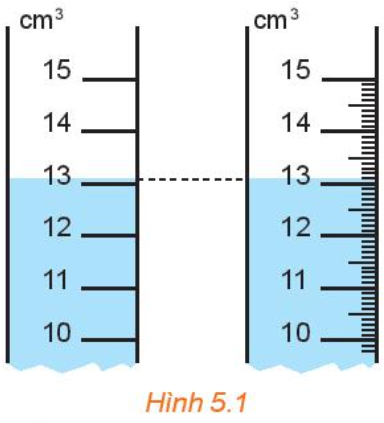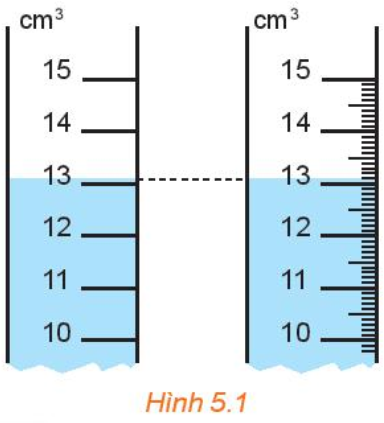Do đó d càng nhỏ thì a càng gần \bar{a} nên d được gọi là độ chính xác của số gần đúng .+ Trong các phép đo, độ chính xác d của số gần đúng bằng một nửa đơn vị của thước đo. Chẳng hạn, một thước đo có chia vạch đến xentimét thì mọi giá trị đo nằm giữa 6,5cm và 7,5cm đều được coi là 7cm. Vì vậy, thước đo có thang đo càng nhỏ thì cho giá trị đo càng chính xác.Ví dụ: Trên hộp bánh có ghi khối lượng tịnh là 500g ± 5g.+ Khối lượng thực tế của hộp bánh \bar{a} là số đúng. Tuy không biết \bar{a} nhưng ta xem khối lượng hộp bánh là 500g nên 500 là số gần đúng cho \bar{a} . Độ chính xác d = 5 (g).+ Giá trị của \bar{a} nằm trong đoạn [500 – 5; 500 + 5] hay [495; 505].b) Sai số tương đốiSai số tương đối của số gần đúng a, kí hiệu là δ a, là tỉ số giữa sai số tuyệt đối và |a|, tức là δ_{a} = \frac{Δ_{a}}{(a)} .Ví dụ: Bao bì của một chai nước suối có ghi thể tích thực là 350ml, biết rằng sai số tuyệt đối là 2ml. Tìm sai số tương đối của chai nước suối.Hướng dẫn giảiTa có a = 350 (ml) và ∆ a = 2 (ml), do đó sai số tương đối là:δ_{a} = \frac{Δ_{a}}{(a)} = \frac{2}{350} \approx 0,57 % .Nhận xét:Nếu \bar{a} = a \pm d thì ∆ a ≤ d, do đó δ_{a} \leq \frac{d}{(a)} . Nếu \frac{d}{(a)} càng nhỏ thì chất lượng của phép đo hay tính toán càng cao. Người ta thường viết sai số tương đối dưới dạng phần trăm.Ví dụ: Trên các chai cồn xịt khuẩn có ghi thể tích thực như sau:+ Chai 1: 500ml ± 3ml;+ Chai 2: 1000ml ± 8ml.Chai nào ghi thể tích thực chính xác hơn tính theo sai số tương đối?Hướng dẫn giải+ Chai 1: a 1 = 500 (ml) và d = 3 (ml), do đó sai số tương đối là:δ_{1} \leq \frac{d}{(a)} = \frac{3}{500} = 0,6 % .+ Chai 2: a 2 = 1000 (ml) và d = 8 (ml), do đó sai số tương đối là:δ_{2} \leq \frac{d}{(a)} = \frac{8}{1000} = 0,8 % .Vì 0,6Vậy chai 1 ghi thể tích thực chính xác hơn chai 2 tính theo sai số tương đối.3. Quy tròn số gần đúngSố thu được sau khi thực hiện làm tròn số được gọi là số quy tròn . Số quy tròn là một số gần đúng của số ban đầu.Ví dụ:+ Số quy tròn của số 12,64 đến hàng đơn vị là 13;+ Số quy tròn của số 500,876 đến hàng phần mười là 500,9.Chú ý:•Đối với chữ số hàng làm tròn:+ Giữ nguyên nếu chữ số ngay bên phải nó nhỏ hơn 5;+ Tăng 1 đơn vị nếu chữ số ngay bên phải nó lớn hơn hoặc bằng 5.•Đối với chữ số sau hàng làm tròn:+ Bỏ đi nếu ở phần thập phân;+ Thay bởi các chữ số 0 nếu ở phần số nguyên.Ví dụ:a) Làm tròn số 5437,56 đến hàng trăm, số 22,758 đến hàng phần mười và số đúng d ∈ [6,5; 7,5) đến hàng đơn vị. Đánh giá sai số tuyệt đối của phép làm tròn số đúng d.b) Cho số gần đúng a = 3,67 với độ chính xác d = 0,02. Số đúng \bar{a} thuộc đoạn nào? Nếu làm tròn số a thì nên làm tròn đến hàng nào? Vì sao?Hướng dẫn giảia) Số quy tròn của số 5437,56 đến hàng trăm là 5400;Số quy tròn của số 22,758 đến hàng phần mười là 22,8;Mọi số đúng d ∈ [6,5; 7,5) khi làm tròn đến hàng đơn vị đều thu được số quy tròn là 7 và sai số tuyệt đối |d – 7| ≤ 0,5.b) Số đúng \bar{a} thuộc đoạn [3,67 – 0,02; 3,67 + 0,02] hay [3,65; 3,69]. Khi làm tròn số gần đúng a ta nên làm tròn đến hàng phần chục do chữ số hàng phần trăm của a là chữ số không chắc chắn đúng.Nhận xét:+ Khi thay số đúng bởi số quy tròn đến một hàng nào đó thì sai số tuyệt đối của số quy tròn không vượt quá nửa đơn vị của hàng làm tròn.+ Cho số gần đúng a với độ chính xác d. Khi được yêu cầu làm tròn số a mà không nói rõ làm tròn đến hàng nào thì ta làm tròn số a đến hàng thấp nhất mà d nhỏ hơn 1 đơn vị của hàng đó.Ví dụ: Cho số gần đúng a = 213 666 với độ chính xác d = 10. Hãy viết số quy tròn của số a.Hướng dẫn giảiVì độ chính xác đến hàng chục (d = 10) nên ta làm tròn đến hàng trăm theo quy tắc làm tròn như trên. Số quy tròn của a là 213700.Xem thêm các bài giải SGK Toán 10 Kết nối tri thức hay, chi tiết khác:Bài tập cuối chương 4Bài 13: Các số đặc trưng đo trung tâm xu thếBài 14: Các số đặc trưng đo độ phân tánBài tập cuối chương 5← Trước Bài viết Tiếp theo Bài viết →Bài liên quan: Giải SGK Toán 10 Bài 1 (Kết nối tri thức): Mệnh đề Giải SGK Toán 10 Bài 2 (Kết nối tri thức): Tập hợp và các phép toán trên tập hợp Giải SGK Toán 10 (Kết nối tri thức) Bài tập cuối chương 1 Giải SGK Toán 10 Bài 3 (Kết nối tri thức): Bất phương trình bậc nhất hai ẩn Giải SGK Toán 10 Bài 4 (Kết nối tri thức): Hệ bất phương trình bậc nhất hai ẩn Giải SGK Toán 10 (Kết nối tri thức) Bài tập cuối chương 2Để lại một bình luận Huỷ trả lời Email của bạn sẽ không được hiển thị công khai. Các trường bắt buộc được đánh dấu * Nhập vào đây... Tên* Email* Trang web Lưu tên của tôi, email, và trang web trong trình duyệt này cho lần bình luận kế tiếp của tôi. ΔBài mới TOP 12 bài Nghị luận về bài thơ Bảo kính cảnh giới 2025 SIÊU HAY Giải sgk Kinh tế Pháp luật 10 Kết nối tri thức | KTPL 10 Kết nối tri thức | Giải Kinh tế và Pháp luật 10 | Giải KTPL 10 | Giải Giáo dục Kinh tế và Pháp luật 10 | Giải bài tập Kinh tế và Pháp luật 10 hay nhất, ngắn gọn TOP 10 bài Nghị luận về bài thơ Mùa xuân chín 2025 SIÊU HAY Mục lục Giải SGK Toán 10 Bài 1 (Kết nối tri thức): Mệnh đề Giải SGK Toán 10 Bài 2 (Kết nối tri thức): Tập hợp và các phép toán trên tập hợp Giải SGK Toán 10 (Kết nối tri thức) Bài tập cuối chương 1 Giải SGK Toán 10 Bài 3 (Kết nối tri thức): Bất phương trình bậc nhất hai ẩn Giải SGK Toán 10 Bài 4 (Kết nối tri thức): Hệ bất phương trình bậc nhất hai ẩn Giải SGK Toán 10 (Kết nối tri thức) Bài tập cuối chương 2 Giải SGK Toán 10 Bài 5 (Kết nối tri thức): Giá trị lượng giác của một góc từ 0 đến 180 Giải SGK Toán 10 Bài 6 (Kết nối tri thức): Hệ thức lượng trong tam giác Giải SGK Toán 10 (Kết nối tri thức) Bài tập cuối chương 3 Giải SGK Toán 10 Bài 7 (Kết nối tri thức): Các khái niệm mở đầu Giải SGK Toán 10 Bài 8 (Kết nối tri thức): Tổng và hiệu của hai vectơ Giải SGK Toán 10 Bài 9 (Kết nối tri thức): Tích của một vecto với một số Giải SGK Toán 10 Bài 10 (Kết nối tri thức): Vectơ trong mặt phẳng tọa độ Giải SGK Toán 10 Bài 11 (Kết nối tri thức): Tích vô hướng của hai vecto Giải SGK Toán 10 (Kết nối tri thức) Bài tập cuối chương 4 Giải SGK Toán lớp 10 Bài 13 (Kết nối tri thức): Các số đặc trưng đo trung tâm xu thế Giải SGK Toán lớp 10 Bài 14 (Kết nối tri thức): Các số đặc trưng đo độ phân tán Giải SGK Toán lớp 10 (Kết nối tri thức) Bài tập cuối chương 5 Giải SGK Toán 10 Bài 15 (Kết nối tri thức): Hàm số Giải SGK Toán 10 Bài 16 (Kết nối tri thức): Hàm số bậc hai Danh mục Chọn Danh mục Bài tập Tiếng anh 12 – Global Success (2) Đề thi Anh (2) Đề thi Toán (7) Địa lí Lớp 10 (76) Địa lí Lớp 11 (31) GDKT-PL Lớp 10 (52) GDKT-PL Lớp 11 (21) GDKT-PL Lớp 12 (16) Giải Chuyên đề học tập Địa Lí 12 – Cánh diều (11) Giải Chuyên đề học tập Địa Lí 12 – Chân trời (13) Giải Chuyên đề học tập Địa Lí 12 – Kết nối (14) Giải Chuyên đề học tập Hóa học 12 – Cánh diều (8) Giải Chuyên đề học tập Hóa học 12 – Chân trời (10) Giải Chuyên đề học tập Hóa học 12 – Kết nối (10) Giải Chuyên đề học tập Lịch sử 12 – Cánh diều (11) Giải Chuyên đề học tập Lịch sử 12 – Chân trời (11) Giải Chuyên đề học tập Lịch sử 12 – Kết nối (11) Giải Chuyên đề học tập Toán 12 – Cánh diều (8) Giải Chuyên đề học tập Toán 12 – Chân trời (11) Giải Chuyên đề học tập Toán 12 – Kết nối (11) Giải Chuyên đề học tập Vật Lí 12 – Cánh diều (7) Giải Chuyên đề học tập Vật Lí 12 – Chân trời (11) Giải Chuyên đề học tập Vật Lí 12 – Kết nối (14) Giải SBT Hóa học 12 – Cánh diều (22) Giải SBT Hóa học 12 – Chân trời (5) Giải SBT Hóa học 12 – Kết nối (5) Giải SBT Toán 12 – Cánh diều (24) Giải SBT Toán 12 – Chân trời (23) Giải SBT Toán 12 – Kết nối (27) Giải SBT Vật Lí 12 – Cánh diều (4) Giải SBT Vật Lí 12 – Chân trời (18) Giải SBT Vật Lí 12 – Kết nối (25) Giải sgk Địa Lí 12 – Cánh diều (31) Giải sgk Địa Lí 12 – Chân trời (40) Giải sgk Địa Lí 12 – Kết nối (36) Giải SGK Hóa học 12 – Cánh diều (23) Giải SGK Hóa học 12 – Chân trời (21) Giải SGK Hóa học 12 – Kết nối (31) Giải sgk Lịch sử 12 – Cánh diều (17) Giải sgk Lịch sử 12 – Chân trời (17) Giải sgk Lịch sử 12 – Kết nối (18) Giải sgk Sinh học 12 – Cánh diều (29) Giải sgk Sinh học 12 – Chân trời (37) Giải sgk Sinh học 12 – Kết nối (36) Giải sgk Tiếng anh 12 – Friends Global (9) Giải SGK Tiếng Anh 12 – Global Success (17) Giải sgk Tiếng anh 12 – iLearn Smart World (16) Giải SGK Toán 12 – Cánh diều (30) Giải SGK Toán 12 – Chân trời (28) Giải SGK Toán 12 – Kết nối (30) Giải SGK Vật Lí 12 – Cánh diều (19) Giải SGK Vật Lí 12 – Chân trời (19) Giải SGK Vật Lí 12 – Kết nối (26) Hoạt động hướng nghiệp (11) Hoạt động trải nghiệm hướng nghiệp 12 (80) Khoa học tự nhiên Lớp 6 (156) Khoa học tự nhiên Lớp 7 (85) Khoa học tự nhiên Lớp 8 (91) Khoa học tự nhiên Lớp 9 (102) Lý thuyết Hóa học 12 – Cánh diều (22) Lý thuyết Hóa học 12 – Chân trời (20) Lý thuyết Hóa học 12 – Kết nối (30) Ngữ pháp Tiếng anh 12 – Global Succes (10) Sinh học Lớp 10 (70) Sinh học Lớp 11 (55) Soạn Văn 12 – Cánh diều (93) Soạn Văn 12 – Chân trời (81) Soạn Văn 12 – Kết nối (75) Tiếng Anh Lớp 10 (24) Tiếng Anh Lớp 11 (49) Tiếng Anh Lớp 12 (10) Tiếng Anh Lớp 2 (60) Tiếng Anh Lớp 3 (141) Tiếng Anh Lớp 4 (48) Tiếng Anh Lớp 5 (46) Tiếng Anh Lớp 6 (113) Tiếng Anh Lớp 7 (89) Tiếng Anh Lớp 8 (32) Tiếng Anh Lớp 9 (44) Tiếng Việt Lớp 2 (339) Tiếng Việt Lớp 3 (203) Tiếng Việt Lớp 4 (327) Tiếng Việt Lớp 5 (355) Toán lớp 10 (46) Toán lớp 2 (186) Toán lớp 3 (229) Toán lớp 4 (260) Toán lớp 5 (147) Toán lớp 6 (247) Toán lớp 7 (152) Toán lớp 8 (164) Toán lớp 9 (107) Trắc nghiệm Địa Lí 12 – Cánh diều (22) Trắc nghiệm Địa Lí 12 – Chân trời (26) Trắc nghiệm Địa Lí 12 – Kết nối (26) Trắc nghiệm Hóa học 12 – Cánh diều (22) Trắc nghiệm Hóa học 12 – Kết nối (30) Trắc nghiệm KTPL 12 – Cánh diều (17) Trắc nghiệm KTPL 12 – Chân trời (16) Trắc nghiệm KTPL 12 – Kết nối (16) Trắc nghiệm Lịch sử 12 – Cánh diều (16) Trắc nghiệm Lịch sử 12 – Chân trời (16) Trắc nghiệm Lịch sử 12 – Kết nối (17) Trắc nghiệm Tin học 12 – Kết nối (37) Từ vựng Tiếng anh 12 – Friends Global (10) Từ vựng Tiếng anh 12 – Global Success (13) Từ vựng Tiếng anh 12 – iLearn Smart World (10) Văn lớp 10 (83) Văn lớp 11 (119) Văn lớp 6 (206) Văn lớp 7 (190) Văn lớp 8 (241) Văn lớp 9 (200) Văn mẫu lớp 12 – Cánh diều (67) Văn mẫu lớp 12 – Chân trời (81) Văn mẫu lớp 12 – Kết nối (126)Copyright © 2026 Học tập lớp 12 | Sách Toán Sitemap Chính sách Giới thiệu Hướng dẫn Thi đấu Kết quả{"prefetch":[{"source":"document","where":{"and":[{"href_matches":"/*"},{"not":{"href_matches":["/wp-*.php","/wp-admin/*","/wp-content/uploads/*","/wp-content/*","/wp-content/plugins/*","/wp-content/themes/astra/*","/*\\?(.+)"]}},{"not":{"selector_matches":"a[rel~=\"nofollow\"]"}},{"not":{"selector_matches":".no-prefetch, .no-prefetch a"}}]},"eagerness":"conservative"}]}Lên đầu trang{"baseUrl":"https://s.w.org/images/core/emoji/17.0.2/72x72/","ext":".png","svgUrl":"https://s.w.org/images/core/emoji/17.0.2/svg/","svgExt":".svg","source":{"concatemoji":"https://lop12.com/wp-includes/js/wp-emoji-release.min.js?ver=6.9.1"}}/*! This file is auto-generated */
const a=JSON.parse(document.getElementById("wp-emoji-settings").textContent),o=(window._wpemojiSettings=a,"wpEmojiSettingsSupports"),s=["flag","emoji"];function i(e){try{var t={supportTests:e,timestamp:(new Date).valueOf()};sessionStorage.setItem(o,JSON.stringify(t))}catch(e){}}function c(e,t,n){e.clearRect(0,0,e.canvas.width,e.canvas.height),e.fillText(t,0,0);t=new Uint32Array(e.getImageData(0,0,e.canvas.width,e.canvas.height).data);e.clearRect(0,0,e.canvas.width,e.canvas.height),e.fillText(n,0,0);const a=new Uint32Array(e.getImageData(0,0,e.canvas.width,e.canvas.height).data);return t.every((e,t)=>e===a[t])}function p(e,t){e.clearRect(0,0,e.canvas.width,e.canvas.height),e.fillText(t,0,0);var n=e.getImageData(16,16,1,1);for(let e=0;e<n.data.length;e++)if(0!==n.data[e])return!1;return!0}function u(e,t,n,a){switch(t){case"flag":return n(e,"\ud83c\udff3\ufe0f\u200d\u26a7\ufe0f","\ud83c\udff3\ufe0f\u200b\u26a7\ufe0f")?!1:!n(e,"\ud83c\udde8\ud83c\uddf6","\ud83c\udde8\u200b\ud83c\uddf6")&&!n(e,"\ud83c\udff4\udb40\udc67\udb40\udc62\udb40\udc65\udb40\udc6e\udb40\udc67\udb40\udc7f","\ud83c\udff4\u200b\udb40\udc67\u200b\udb40\udc62\u200b\udb40\udc65\u200b\udb40\udc6e\u200b\udb40\udc67\u200b\udb40\udc7f");case"emoji":return!a(e,"\ud83e\u1fac8")}return!1}function f(e,t,n,a){let r;const o=(r="undefined"!=typeof WorkerGlobalScope&&self instanceof WorkerGlobalScope?new OffscreenCanvas(300,150):document.createElement("canvas")).getContext("2d",{willReadFrequently:!0}),s=(o.textBaseline="top",o.font="600 32px Arial",{});return e.forEach(e=>{s[e]=t(o,e,n,a)}),s}function r(e){var t=document.createElement("script");t.src=e,t.defer=!0,document.head.appendChild(t)}a.supports={everything:!0,everythingExceptFlag:!0},new Promise(t=>{let n=function(){try{var e=JSON.parse(sessionStorage.getItem(o));if("object"==typeof e&&"number"==typeof e.timestamp&&(new Date).valueOf()<e.timestamp+604800&&"object"==typeof e.supportTests)return e.supportTests}catch(e){}return null}();if(!n){if("undefined"!=typeof Worker&&"undefined"!=typeof OffscreenCanvas&&"undefined"!=typeof URL&&URL.createObjectURL&&"undefined"!=typeof Blob)try{var e="postMessage("+f.toString()+"("+[JSON.stringify(s),u.toString(),c.toString(),p.toString()].join(",")+"));",a=new Blob([e],{type:"text/javascript"});const r=new Worker(URL.createObjectURL(a),{name:"wpTestEmojiSupports"});return void(r.onmessage=e=>{i(n=e.data),r.terminate(),t(n)})}catch(e){}i(n=f(s,u,c,p))}t(n)}).then(e=>{for(const n in e)a.supports[n]=e[n],a.supports.everything=a.supports.everything&&a.supports[n],"flag"!==n&&(a.supports.everythingExceptFlag=a.supports.everythingExceptFlag&&a.supports[n]);var t;a.supports.everythingExceptFlag=a.supports.everythingExceptFlag&&!a.supports.flag,a.supports.everything||((t=a.source||{}).concatemoji?r(t.concatemoji):t.wpemoji&&t.twemoji&&(r(t.twemoji),r(t.wpemoji)))});
//# sourceURL=https://lop12.com/wp-includes/js/wp-emoji-loader.min.jswindow.lazyLoadOptions=Object.assign({},{threshold:300},window.lazyLoadOptions||{});!function(t,e){"object"==typeof exports&&"undefined"!=typeof module?module.exports=e():"function"==typeof define&&define.amd?define(e):(t="undefined"!=typeof globalThis?globalThis:t||self).LazyLoad=e()}(this,function(){"use strict";function e(){return(e=Object.assign||function(t){for(var e=1;e<arguments.length;e++){var n,a=arguments[e];for(n in a)Object.prototype.hasOwnProperty.call(a,n)&&(t[n]=a[n])}return t}).apply(this,arguments)}function o(t){return e({},at,t)}function l(t,e){return t.getAttribute(gt+e)}function c(t){return l(t,vt)}function s(t,e){return function(t,e,n){e=gt+e;null!==n?t.setAttribute(e,n):t.removeAttribute(e)}(t,vt,e)}function i(t){return s(t,null),0}function r(t){return null===c(t)}function u(t){return c(t)===_t}function d(t,e,n,a){t&&(void 0===a?void 0===n?t(e):t(e,n):t(e,n,a))}function f(t,e){et?t.classList.add(e):t.className+=(t.className?" ":"")+e}function _(t,e){et?t.classList.remove(e):t.className=t.className.replace(new RegExp("(^|\\s+)"+e+"(\\s+|$)")," ").replace(/^\s+/,"").replace(/\s+$/,"")}function g(t){return t.llTempImage}function v(t,e){!e||(e=e._observer)&&e.unobserve(t)}function b(t,e){t&&(t.loadingCount+=e)}function p(t,e){t&&(t.toLoadCount=e)}function n(t){for(var e,n=[],a=0;e=t.children[a];a+=1)"SOURCE"===e.tagName&&n.push(e);return n}function h(t,e){(t=t.parentNode)&&"PICTURE"===t.tagName&&n(t).forEach(e)}function a(t,e){n(t).forEach(e)}function m(t){return!!t[lt]}function E(t){return t[lt]}function I(t){return delete t[lt]}function y(e,t){var n;m(e)||(n={},t.forEach(function(t){n[t]=e.getAttribute(t)}),e[lt]=n)}function L(a,t){var o;m(a)&&(o=E(a),t.forEach(function(t){var e,n;e=a,(t=o[n=t])?e.setAttribute(n,t):e.removeAttribute(n)}))}function k(t,e,n){f(t,e.class_loading),s(t,st),n&&(b(n,1),d(e.callback_loading,t,n))}function A(t,e,n){n&&t.setAttribute(e,n)}function O(t,e){A(t,rt,l(t,e.data_sizes)),A(t,it,l(t,e.data_srcset)),A(t,ot,l(t,e.data_src))}function w(t,e,n){var a=l(t,e.data_bg_multi),o=l(t,e.data_bg_multi_hidpi);(a=nt&&o?o:a)&&(t.style.backgroundImage=a,n=n,f(t=t,(e=e).class_applied),s(t,dt),n&&(e.unobserve_completed&&v(t,e),d(e.callback_applied,t,n)))}function x(t,e){!e||0<e.loadingCount||0<e.toLoadCount||d(t.callback_finish,e)}function M(t,e,n){t.addEventListener(e,n),t.llEvLisnrs[e]=n}function N(t){return!!t.llEvLisnrs}function z(t){if(N(t)){var e,n,a=t.llEvLisnrs;for(e in a){var o=a[e];n=e,o=o,t.removeEventListener(n,o)}delete t.llEvLisnrs}}function C(t,e,n){var a;delete t.llTempImage,b(n,-1),(a=n)&&--a.toLoadCount,_(t,e.class_loading),e.unobserve_completed&&v(t,n)}function R(i,r,c){var l=g(i)||i;N(l)||function(t,e,n){N(t)||(t.llEvLisnrs={});var a="VIDEO"===t.tagName?"loadeddata":"load";M(t,a,e),M(t,"error",n)}(l,function(t){var e,n,a,o;n=r,a=c,o=u(e=i),C(e,n,a),f(e,n.class_loaded),s(e,ut),d(n.callback_loaded,e,a),o||x(n,a),z(l)},function(t){var e,n,a,o;n=r,a=c,o=u(e=i),C(e,n,a),f(e,n.class_error),s(e,ft),d(n.callback_error,e,a),o||x(n,a),z(l)})}function T(t,e,n){var a,o,i,r,c;t.llTempImage=document.createElement("IMG"),R(t,e,n),m(c=t)||(c[lt]={backgroundImage:c.style.backgroundImage}),i=n,r=l(a=t,(o=e).data_bg),c=l(a,o.data_bg_hidpi),(r=nt&&c?c:r)&&(a.style.backgroundImage='url("'.concat(r,'")'),g(a).setAttribute(ot,r),k(a,o,i)),w(t,e,n)}function G(t,e,n){var a;R(t,e,n),a=e,e=n,(t=Et[(n=t).tagName])&&(t(n,a),k(n,a,e))}function D(t,e,n){var a;a=t,(-1<It.indexOf(a.tagName)?G:T)(t,e,n)}function S(t,e,n){var a;t.setAttribute("loading","lazy"),R(t,e,n),a=e,(e=Et[(n=t).tagName])&&e(n,a),s(t,_t)}function V(t){t.removeAttribute(ot),t.removeAttribute(it),t.removeAttribute(rt)}function j(t){h(t,function(t){L(t,mt)}),L(t,mt)}function F(t){var e;(e=yt[t.tagName])?e(t):m(e=t)&&(t=E(e),e.style.backgroundImage=t.backgroundImage)}function P(t,e){var n;F(t),n=e,r(e=t)||u(e)||(_(e,n.class_entered),_(e,n.class_exited),_(e,n.class_applied),_(e,n.class_loading),_(e,n.class_loaded),_(e,n.class_error)),i(t),I(t)}function U(t,e,n,a){var o;n.cancel_on_exit&&(c(t)!==st||"IMG"===t.tagName&&(z(t),h(o=t,function(t){V(t)}),V(o),j(t),_(t,n.class_loading),b(a,-1),i(t),d(n.callback_cancel,t,e,a)))}function $(t,e,n,a){var o,i,r=(i=t,0<=bt.indexOf(c(i)));s(t,"entered"),f(t,n.class_entered),_(t,n.class_exited),o=t,i=a,n.unobserve_entered&&v(o,i),d(n.callback_enter,t,e,a),r||D(t,n,a)}function q(t){return t.use_native&&"loading"in HTMLImageElement.prototype}function H(t,o,i){t.forEach(function(t){return(a=t).isIntersecting||0<a.intersectionRatio?$(t.target,t,o,i):(e=t.target,n=t,a=o,t=i,void(r(e)||(f(e,a.class_exited),U(e,n,a,t),d(a.callback_exit,e,n,t))));var e,n,a})}function B(e,n){var t;tt&&!q(e)&&(n._observer=new IntersectionObserver(function(t){H(t,e,n)},{root:(t=e).container===document?null:t.container,rootMargin:t.thresholds||t.threshold+"px"}))}function J(t){return Array.prototype.slice.call(t)}function K(t){return t.container.querySelectorAll(t.elements_selector)}function Q(t){return c(t)===ft}function W(t,e){return e=t||K(e),J(e).filter(r)}function X(e,t){var n;(n=K(e),J(n).filter(Q)).forEach(function(t){_(t,e.class_error),i(t)}),t.update()}function t(t,e){var n,a,t=o(t);this._settings=t,this.loadingCount=0,B(t,this),n=t,a=this,Y&&window.addEventListener("online",function(){X(n,a)}),this.update(e)}var Y="undefined"!=typeof window,Z=Y&&!("onscroll"in window)||"undefined"!=typeof navigator&&/(gle|ing|ro)bot|crawl|spider/i.test(navigator.userAgent),tt=Y&&"IntersectionObserver"in window,et=Y&&"classList"in document.createElement("p"),nt=Y&&1<window.devicePixelRatio,at={elements_selector:".lazy",container:Z||Y?document:null,threshold:300,thresholds:null,data_src:"src",data_srcset:"srcset",data_sizes:"sizes",data_bg:"bg",data_bg_hidpi:"bg-hidpi",data_bg_multi:"bg-multi",data_bg_multi_hidpi:"bg-multi-hidpi",data_poster:"poster",class_applied:"applied",class_loading:"litespeed-loading",class_loaded:"litespeed-loaded",class_error:"error",class_entered:"entered",class_exited:"exited",unobserve_completed:!0,unobserve_entered:!1,cancel_on_exit:!0,callback_enter:null,callback_exit:null,callback_applied:null,callback_loading:null,callback_loaded:null,callback_error:null,callback_finish:null,callback_cancel:null,use_native:!1},ot="src",it="srcset",rt="sizes",ct="poster",lt="llOriginalAttrs",st="loading",ut="loaded",dt="applied",ft="error",_t="native",gt="data-",vt="ll-status",bt=[st,ut,dt,ft],pt=[ot],ht=[ot,ct],mt=[ot,it,rt],Et={IMG:function(t,e){h(t,function(t){y(t,mt),O(t,e)}),y(t,mt),O(t,e)},IFRAME:function(t,e){y(t,pt),A(t,ot,l(t,e.data_src))},VIDEO:function(t,e){a(t,function(t){y(t,pt),A(t,ot,l(t,e.data_src))}),y(t,ht),A(t,ct,l(t,e.data_poster)),A(t,ot,l(t,e.data_src)),t.load()}},It=["IMG","IFRAME","VIDEO"],yt={IMG:j,IFRAME:function(t){L(t,pt)},VIDEO:function(t){a(t,function(t){L(t,pt)}),L(t,ht),t.load()}},Lt=["IMG","IFRAME","VIDEO"];return t.prototype={update:function(t){var e,n,a,o=this._settings,i=W(t,o);{if(p(this,i.length),!Z&&tt)return q(o)?(e=o,n=this,i.forEach(function(t){-1!==Lt.indexOf(t.tagName)&&S(t,e,n)}),void p(n,0)):(t=this._observer,o=i,t.disconnect(),a=t,void o.forEach(function(t){a.observe(t)}));this.loadAll(i)}},destroy:function(){this._observer&&this._observer.disconnect(),K(this._settings).forEach(function(t){I(t)}),delete this._observer,delete this._settings,delete this.loadingCount,delete this.toLoadCount},loadAll:function(t){var e=this,n=this._settings;W(t,n).forEach(function(t){v(t,e),D(t,n,e)})},restoreAll:function(){var e=this._settings;K(e).forEach(function(t){P(t,e)})}},t.load=function(t,e){e=o(e);D(t,e)},t.resetStatus=function(t){i(t)},t}),function(t,e){"use strict";function n(){e.body.classList.add("litespeed_lazyloaded")}function a(){console.log("[LiteSpeed] Start Lazy Load"),o=new LazyLoad(Object.assign({},t.lazyLoadOptions||{},{elements_selector:"[data-lazyloaded]",callback_finish:n})),i=function(){o.update()},t.MutationObserver&&new MutationObserver(i).observe(e.documentElement,{childList:!0,subtree:!0,attributes:!0})}var o,i;t.addEventListener?t.addEventListener("load",a,!1):t.attachEvent("onload",a)}(window,document);window.litespeed_ui_events=window.litespeed_ui_events||["mouseover","click","keydown","wheel","touchmove","touchstart"];var urlCreator=window.URL||window.webkitURL;function litespeed_load_delayed_js_force(){console.log("[LiteSpeed] Start Load JS Delayed"),litespeed_ui_events.forEach(e=>{window.removeEventListener(e,litespeed_load_delayed_js_force,{passive:!0})}),document.querySelectorAll("iframe[data-litespeed-src]").forEach(e=>{e.setAttribute("src",e.getAttribute("data-litespeed-src"))}),"loading"==document.readyState?window.addEventListener("DOMContentLoaded",litespeed_load_delayed_js):litespeed_load_delayed_js()}litespeed_ui_events.forEach(e=>{window.addEventListener(e,litespeed_load_delayed_js_force,{passive:!0})});async function litespeed_load_delayed_js(){let t=[];for(var d in document.querySelectorAll('script[type="litespeed/javascript"]').forEach(e=>{t.push(e)}),t)await new Promise(e=>litespeed_load_one(t[d],e));document.dispatchEvent(new Event("DOMContentLiteSpeedLoaded")),window.dispatchEvent(new Event("DOMContentLiteSpeedLoaded"))}function litespeed_load_one(t,e){console.log("[LiteSpeed] Load ",t);var d=document.createElement("script");d.addEventListener("load",e),d.addEventListener("error",e),t.getAttributeNames().forEach(e=>{"type"!=e&&d.setAttribute("data-src"==e?"src":e,t.getAttribute(e))});let a=!(d.type="text/javascript");!d.src&&t.textContent&&(d.src=litespeed_inline2src(t.textContent),a=!0),t.after(d),t.remove(),a&&e()}function litespeed_inline2src(t){try{var d=urlCreator.createObjectURL(new Blob([t.replace(/^(?:)?$/gm,"$1")],{type:"text/javascript"}))}catch(e){d="data:text/javascript;base64,"+btoa(t.replace(/^(?:)?$/gm,"$1"))}return d}var litespeed_vary=document.cookie.replace(/(?:(?:^|.*;\s*)_lscache_vary\s*\=\s*([^;]*).*$)|^.*$/,"");litespeed_vary||fetch("/wp-content/plugins/litespeed-cache/guest.vary.php",{method:"POST",cache:"no-cache",redirect:"follow"}).then(e=>e.json()).then(e=>{console.log(e),e.hasOwnProperty("reload")&&"yes"==e.reload&&(sessionStorage.setItem("litespeed_docref",document.referrer),window.location.reload(!0))});$